(School of Management, Xi'an Univ. of Arch. & Tech. Xi'an 710055, China)
utility tunnel; PPP mode; BP neural network; intuitionistic trapezoidal fuzzy numbers; TOPSIS method
DOI: 10.15986/j.1006-7930.2018.01.020
采用PPP模式建设和运营地下综合管廊可以缓解政府的财政压力.PPP模式分类众多,各个模式的运作方式均存在差异,采用合适的PPP模式对地下综合管廊项目进行建设和运营十分必要.提出PPP模式的两阶段模式选择模型.首先,分别建立二级和三级PPP模式选择的指标体系,应用BP神经网络为具体的地下综合管廊项目选择出合适的二级PPP模式; 然后,运用改进的TOPSIS法,即直觉梯形模糊TOPSIS法求得选出的二级PPP模式下各三级模式的贴近度,基于贴近度大小对三级PPP模式进行排序; 最后以郑州市地下综合管廊PPP项目为例,通过建立的两阶段模式选择模型对该项目适宜采用的PPP模式进行选择.结果表明,模型的预测性能良好,所得模型对于地下综合管廊PPP项目进行模式选择具有较强的指导意义和操作性.
Using PPP mode to construct and operate utility tunnel can alleviate the financial pressure of government. PPP mode has many classifications and each way of working of them is different, so it is necessary to construct and operate the utility tunnel project with the appropriate PPP mode. A two-stage mode selection model for PPP mode was proposed. Firstly, the index system of selection of secondary and tertiary PPP mode is established respectively, by using BP neural network to choose the appropriate secondary PPP mode for specific utility tunnel project. Then, an improved TOPSIS method was used, namely intuitionistic trapezoidal fuzzy TOPSPS method to find the closeness to the tertiary modes which belong to the selected secondary PPP mode and then sort the tertiary PPP mode by closeness. Finally, the effectiveness of the PPP mode selection model is further illustrated by an example. The results show that the model has good predictive and strong guiding significance and operability for the mode selection of utility tunnel PPP project.
传统直埋管线的扩容和维修比较困难,而且不同管线单位的埋设时间不同,这些都导致道路被反复开挖,严重影响城市环境和道路交通.为了解决这一问题,世界上比较认同的做法是采用地下综合管廊对市政管线进行敷设.地下综合管廊建设成本巨大,给政府带来了巨大的财政压力,所以我国现阶段大力提倡采用PPP模式建设地下综合管廊.PPP是在基础设施及公共服务领域建立的一种长期合作关系[1],在实际应用中衍生出了众多运作方式不同的具体模式,因此需要理清PPP模式的种类并根据项目的特点来选择合适的PPP模式.对此,王灏[2]提出了PPP模式三级结构分类法,本文在参考以往研究的基础上建立了新的PPP模式三级分类,以求最大程度涵盖所有PPP模式,如图1所示.
图1 PPP模式三级分类
Fig.1 Three-stage classification of PPP mode
我国基础设施建设仍然存在盲目采用BOT模式的现象,且对于PPP模式选择的相关研究较少,因此本文构建了地下综合管廊PPP项目模式选择模型,该模型可以较准确地对项目适宜采用的二级和三级PPP模式进行选择,从而为地下综合管廊PPP项目顺利运行提供指导.
在项目模式选择方面,国外学者的研究相对较早,Cheung[3]和Chang[4]均采用多属性分析法对项目模型进行选择,并且Chang指出,应用多属性分析法选择项目模式时,需要综合考虑风险分担、契约不完备性和数据充足性等因素.Thomas[5]和Chan[6]在Cheung和Chang研究的基础上提出了模糊选择模型以解决多属性分析法模式选择标准模糊的问题.Luu[7]等提出了项目模式选择的案例式推理模型.Yuan[8]等通过文献分析及案例研究的方法找出了影响PPP模式选择的15个指标.Thomas等指出,政府的经济政策、社会对产品和服务的长期需求、私人部门的实力、运营效率、税率、服务质量等是决定PPP模式选择的因素[9].
国内对于项目模式选择的研究起步较晚,胡振[10]研究了PPP项目模式选择与项目领域、特许经营期、收益方式和VFM效果这四个因素间的关系.简迎辉等[11]认为项目自身特点、政府部门能力及经验偏好和法律政策等因素都会影响PPP模式选择.杨卫华[12]等构建了以所有权转移效益、经营权控制程度、公私合作程度为坐标的三维框
架,识别出了PPP模式选择的三条路径.
综上所述,国内外对PPP模式选择的相关研究大多是针对整个基础设施领域选择二级PPP模式,而针对地下综合管廊的三级PPP模式选择研究甚少,鉴于此,本文首先针对地下综合管廊项目建立了二级和三级PPP模式选择指标体系,然后通过BP神经网络和直觉梯形模糊TOPSIS法为地下综合管廊项目选择合适的三级PPP模式.
采用依次确定二级和三级PPP模式的方法,首先建立二级PPP模式选择的指标体系,再针对不同的二级模式分别建立对应的三级模式选择指标体系,保证模式选择结果的准确性.
地下综合管廊属于大型基础设施,项目最终的所有权不能属于私人部门,因此将私有化类PPP模式排除,考虑到项目类型分为新建和存量,模块式外包和BOT模式只适用于新建项目,TOT模式只适用于存量项目,而整体式外包同时适用于新建和存量项目,故本文将二级PPP模式分为5类:模块式外包、整体式外包(新建)、整体式外包(存量)、BOT、TOT.
从项目全生命周期角度来看,存量项目可看作新建项目生命周期的一部分,因此,影响前者PPP模式选择的因素包含于影响后者PPP模式选择的因素之中,所以可先确定出影响新建地下综合管廊项目二级PPP模式选择的指标,再针对存量项目从中选择.在前人研究的基础上,结合地下综合管廊的特点,初选出了影响新建地下综合管廊项目二级PPP模式选择的25个指标,如表1所示.
表1 新建地下综合管廊PPP项目二级PPP模式选择初选指标
Tab.1 Primary index of secondary PPP mode of new utility tunnel project
为保证指标体系的准确性,本文采用聚类-灰色关联分析法,先通过聚类分析消除相关性大的指标,然后通过灰色关联分析筛选出重要性较大的指标,从而确定出最终的指标体系.
通过邀请5位PPP领域专家和5位地下综合管廊领域专家对初选出的25个指标进行打分(打分标准采用李克特七级量表),然后采用min-max标准化对原始数据进行线性变换,公式为:
x'ij=(xij-min(xij))/(max(xij)-min(xij))(极大型指标)
x'ij=(max(xij)-xij)/(max(xij)-min(xij))(极小型指标)
将数据标准化后,通过SPSS 19.0软件的ward's method对初选的25个指标进行系统聚类分析,度量标准区间使用平方Euclidean距离,最终得到如表2所示的聚类结果.
表2 聚类分析结果
Tab.2 Results of cluster analysis
对表2聚类结果进行单因素方差分析,结果显示聚类数为7的结果通过显著性检验,结合各指标的现实意义得出,将指标分为7类的聚类结果是合理的,因此最终选用该聚类结果进入下一步筛选.
按照以下四个步骤,分别对聚类结果的7组指标进行灰色关联分析,这里以第3组为例:
(1)以上一节中标准化后的指标为矩阵求差序列
Δxij(k)=|x'i(k)-xx'j(k)|
式中:i,j=6,23,24,25且i≠j,k=1,2…10.
(2)求关联系数
ξij(k)=(Δmin+ρΔmax)/(Δxij(k)+ρΔmax)
式中:i,j=6,23,24,25且i≠j,k=1,2…10.ρ∈[0,1]为分辨系数,常取0.5.
(3)计算关联度
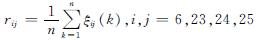且i≠j,k=1,2…10
(4)计算重要性并排序
第3组指标的重要性矩阵为A=(rij)4×3,每一行的均值(
即为指标x6,x23,x24,x25的重要度,重要度越大,说明该指标对系统的影响越大,可根据实际情况将重要度较小的指标剔除出去,留下对系统影响较大的指标.
分别对聚类分析求得的7组指标进行灰色关联分析,结果见表3.
表3 灰色关联分析结果
Tab.3 Results of Grey Correlation
经过聚类-灰色关联分析,最终确定了新建地下综合管廊PPP项目二级PPP模式选择的指标体系,见表4.
表4 新建地下综合管廊PPP项目二级PPP模式选择指标体系
Tab.4 Index system of secondary mode selection of new utility tunnel PPP project
根据存量和新建项目的包含关系,从表4中选择存量地下综合管廊PPP项目模式选择指标体系,由于存量项目不需考虑地下综合管廊前期建设以及管线入廊等问题,故排除x1、x2、x3、x6、x12五个指标,选择出的指标体系如表5所示.
在三级PPP模式选择指标体系的构建上,本文借鉴了Yuan[8]和李英攀[13]的相关研究,并通过深入分析各三级PPP模式的含义,建立了一套三级PPP模式选择指标体系,如表6所示.
表5 存量地下综合管廊PPP项目二级模式选择指标体系
Tab.5 Index system of secondary mode selection of completed utility tunnel
表6 三级PPP模式选择指标体系
Tab.6 Index system of tertiary PPP mode
对PPP模式的选择分为两个阶段,第一阶段采用BP神经网络对二级PPP模式进行选择,BP神经网络拥有较强的非线性映射能力和泛化能力,适用于在多因素影响下对二级PPP模式进行选择; 第二阶段采用直觉梯形模糊TOPSIS法针对选择出的二级PPP模式下的三级模式进行选择,既可以降低专家评价的主观性,充分利用原始数据信息,又能集中反映每一种三级PPP模式的适用度.
本文采用1个输入层、1个隐层和1个输出层的三层神经网络.表7中14个指标作为输入指标,因此输入层神经元数为Pn=14.5类PPP二级模式作为输出,由于22<5<23,故输出层神经元数为3个,用(x,y,z)的形式表示5个二级模式的期望输出值,x,y,z=0,1,其中(1,0,0)代表模块式外包;(0,1,0)代表整体式外包(新建);(0,0,1)代表整体式外包(存量);(1,0,1)代表BOT模式;(0,1,1)代表TOT模式.
隐层神经元个数的确定根据经验公式:
Pm=(Pn+r)1/2+α
式中:Pm为隐层神经元数,Pn为输入层神经元数,r为输出层神经元数,α为[1,10]之间的整数.通过对模型的反复训练比较得出,隐层神经元数为10时BP神经网络的收敛效果最好.因此,本文建立了拓扑结构为14-10-3的BP神经网络模型.
邀请4位政府部门专家、4位地下综合管廊领域专家和5位PPP领域专家针对5类PPP二级模式按照表7对各指标进行评价打分,作为BP神经网络输入层的输入值.这里将数据标准化到[-1,1]区间作为输入变量,公式为
x'ij=(2[xij-minj(xij)])/(maxj(xij)-minj(xij))-1
式中:xij为第i个指标原始值; maxj(xij )为第i个指标的得分最大值; minj(xij )为第i个指标的得分最小值; x'ij为第i个指标归一化后的值.
表7 神经网络输入变量表
Tab.7 Input variables of neural network
选取5种二级PPP模式各8组数据作为训练数据,其余各5组数据用作测试验证.将40组归一化后的训练数据输入模型,对BP神经网络进行多次训练,将误差较小的一次保存用来测试.最终选取了训练次数为573,累计误差为9.971 6×10-4的BP神经网络模型用作PPP模式选择,如图2.
图2 BP神经网络性能曲线图
Fig.2 Graph of BP neural network
由于输出向量x,y,z的值在[0,1]区间,且存在误差,本文规定如果输出向量在[0,0.4]区间则近似看作0,如果在[0.6,1]区间则近似看作1.
将剩余的5种PPP二级模式共25组数据归一化后输入训练好的BP神经网络模型进行测试验证,结果表明预测精度为92.89%,表明该模式选择模型具有较高的精度.
传统的TOPSIS方法忽视了专家获得信息的不确定性以及专家权重,本文引入直觉梯形模糊数,将其与TOPSIS法相结合来解决该多属性群决策问题,考虑了专家权重,降低了专家评价的主观偏好和模糊性.
(1)确定专家群体偏好值r'ij
设r(k)ij=〈(a(k)ij1,a(k)ij2,a(k)ij4),(b(k)ij1,b(k)ij2,b(k)ij3,b(k)ij4)〉(i=1,2,…,m,j=1,2,…,n,k=1,2,…,l)是第k个专家针对第i个方案给出的第j个指标的偏好值,则专家群体关于该方案上该指标的偏好均值r(k)ij可通过TrIFA算子求得:
这里自定义运算:
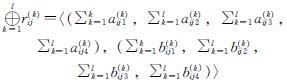
(2)计算r(k)ij与群体平均偏好r'ij的相似度
每位专家与专家群体平均偏好r'ij之间的距离为:
D(r(k)ij,r'ij)=(1/(12)(∑4c=1((a'ijc-a(k)ijc)+(b'ijc-b(k)ijc)2)+∑d=1,3((a'ijd-a(k)ijd)(a'ij(d+1)-a(k)ij(d+1))+(b'ijd-b(k)ijd)(b'ij(d+1)-b(k)ij(d+1)))))1/2(2)
与平均偏好的相似度为:
S(r(k)ij,r'ij )=1-(D(r(k)ij,r'ij ))/((∑lk=1D(r(k)ij,r'ij ))(3)
(3)确定直觉梯形模糊决策矩阵R=(rij)m×n
计算专家权重ω(k)ij:
ω(k)ij=(S(r(k)ij,r'ij ))/(∑lk=1(S(r(k)ij,r'ij )))(4)
通过TrIFWA算子确定出直觉梯形模糊决策矩阵R=(rij)m×n,将每个专家的个人决策信息集结为专家群体决策信息,公式为
(4)确定指标标准化的期望决策权重
每位专家针对每个指标以直觉梯形模糊数的形式给出指标重要性评价,设ξ(k)j表示第k位专家对指标j的重要性评价值,则通过TrIFWA算子可求出第i个方案关于指标j的权重ξij:
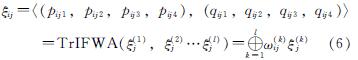(6)
期望权重:
EV(ξij)=1/8(∑<sub>d=1(pijd+qijd))(7)
标准化的期望决策权重为
ξ'ij=(EV(ξij))/(∑nj=1EV(ξij))(8)
(5)计算各个方案的加权正负分离测度
首先确定正理想解o+和负理想解o-:
o+=(o+1,o+2…o+k)T
o-=(o-1,o-2…o-k)T
当第j个指标为收益型指标时,
o+j=〈(maxi,aij1,maxi,aij2,maxi,aij3,maxi,aij4 ),(maxi,aij1,maxi,bij2,maxi,bij3,maxi,bij4)〉
o-j=〈(mini,aij1,mini,aij2,mini,aij3,mini,aij4 ),(mini,aij1,mini,bij2mini,bij3,mini,bij4)〉(9)
当第j个指标为成本型指标时,
o+j=〈(mini,aij1,mini,aij2mini,aij3,mini,aij4 ),(mini,aij1,mini,bij2mini,bij3,mini,bij4)〉
o+j=〈(maxi,aij1,maxi,aij2,maxi,aij3,maxi,aij4 ),(maxi,aij1,maxi,bij2maxi,bij3,maxi,bij4)〉(10)
第i个方案的正分离测度S+i和负分离测度S-i为:
S+i=∑nj=1ξ'ijD(rij,o+j )
S-i=∑nj=1ξ'ijD(rij,o+j )(11)
(6)求相对贴近度Zi并排序
Zi=(S-i)/(S-i+S+i)(12)
贴近度越大,则该方案越优.
郑州市中心城区地下综合管廊工程位于郑州市二七商业区,包含二七路、太康路两条道路,呈“十字”形分布,共需建设地下综合管廊3.129 km(其中主线2.079 km,支线1.05 km).项目的总投资约60 405.2万元,其中包括中央财政补贴暂定为12 500万元,采用PPP模式投资部分为47 905.2万元,采用BOT模式运作,合作期限30 a.
首先邀请10位专家针对当地具体情况按照表7对14个指标进行打分,其中政府部门3位,地下综合管廊领域专家3位,PPP模式领域专家4位.项目类型取1(新建项目),其余13个指标采取归一化后取平均值的方法确定每个指标的得分,确定输入矩阵为S=(1,-0.6,-0.2,-0.6,0.6,0.8,0.6,0.4,0.6,0.2,0.6,-0.6,0.6,-0.4),将其输入训练好的结构为14-10-3的BP神经网络模型中,实际输出为(0.997 8,0.006 4,0.918 2),可近似看作(1,0,1),对应PPP二级模式中的BOT模式,与项目在实际中选择的模式相符合.
其次运用直觉梯形模糊TOPSIS法针对BOT模式下的三级PPP模式进行选择.分别用Oi(i=1,2,…,6)表示BOT模式下的6个PPP模式,用Cj(j=1,2,…,8)表示其模式选择指标.邀请k=8位专家对该问题进行评价,评价时参考Jun Ye[14]建立的语言变量与直觉梯形模糊数的转化标准,见表8.
运用公式(1)～(5)计算出直觉梯形模糊决策矩阵R,表9为每位专家针对每个指标以直觉梯形模糊数的形式给出的指标重要性评价.
表8 语言变量和直觉梯形模糊数的转化标准
Tab.8 Transformation standard between linguistic variables and intuitionistic trapezoidal fuzzy number
表9 指标重要性评价
Tab.9 Importance evaluation of index
通过公式(6)～(10)计算出正负理想解,并运用公式(11)～(12)计算各三级PPP模式的正负分离测度和相对贴近度,如表 10所示.
表 10 正负分离测度和相对贴近度
Tab.10 Positive and negative separation measure and relative close degree
将相对贴近度按照大小排序,Z4>Z3>Z5>Z2>Z6>Z1,所以最优方案为DBTO模式.
(1)选择合适的PPP模式建设和运营地下综合管廊直接关系着项目的成功与否.研究建立了两阶段PPP模式选择模型,第一阶段通过BP神经网络对二级PPP模式进行选择,第二阶段运用直觉梯形模糊数与TOPSIS结合的方法选择三级PPP模式,降低了决策的主观性和模糊性,减少了决策信息的损失,使选择结果更加客观合理.
(2)通过案例分析可知,不同的三级PPP模式对同一项目来说适用度各不相同,所以在建设运营地下综合管廊项目时不能仅靠以往经验选择PPP模式,而要结合项目实际情况和具体特点,通过合理的方式选择最合适的三级PPP模式,以确保项目顺利实施.
(3)指标体系在地下综合管廊PPP项目模式选择中起着至关重要的作用,本文建立的二级和三级PPP模式选择指标体系是在前人研究的基础上,结合对地下综合管廊自身特点的分析建立的,在指标种类上可能会存在缺失或冗余,应在今后的研究中逐步加以改善.
