基金项目:教育部留学回国人员科研启动基金(教外司留[2014]1685号); 西安市碑林区2016年科技计划项目(GX1603)
第一作者:于军琪(1969-),男,博士,教授,主要从事智能建筑与建筑节能方面的研究.E-mail:Junqiyu@126.com 通迅作者:王胤钧(1991-),男,硕士,主要从事建筑电气与智能化方面的研究. E-mail:583798462@qq.com
(1.西安建筑科技大学 信控学院,陕西 西安 710055; 2.陕西省建筑设计研究院有限责任公司,陕西 西安 710018 )
(1.School of Information and Control Engineering, Xi'an Univ. of Arch. & Tech., Xi'an 710055,China; 2. Shaanxi Architectural Design and Research Institute Co., Ltd., Xi'an 710018, China)
ice-storage air-conditioning system; running costs; energy consumption; particle swarm optimization; optimization parameters
DOI: 10.15986/j.1006-7930.2018.01.023
冰蓄冷空调系统可以平衡电网压力,达到“移峰填谷”的作用,为了推广冰蓄冷空调的使用,提高系统的经济效益和节能效果具有重要意义.通过建立冰蓄冷空调系统的运行模型,表示出冰蓄冷空调系统的日运行费用和日运行能耗.通过TRNSYS软件对目标建筑的模拟得到目标建筑冷负荷.依据目标建筑冷负荷,设定系统制冷主机每小时的荷载率,建立冰蓄冷空调系统节能、经济运行的多目标函数模型,并使用粒子群算法对模型求解得到系统优化运行参数.通过实例分析:与现阶段的运行策略相比较,使用得到的优化运行参数指导系统运行可以为用户节约10.2%的运行费用,同时可以降低15.2%的电能损失.
Ice-storage air-conditioning system can balance the grid pressure to achieve “peak load shifting” effect. In order to promote the use of ice storage air-conditioning, enhancing economic efficiency and energy-saving effect of the system is important. Through the establishment of ice storage air-conditioning system operation model daily running costs and daily energy consumption of ice-storage air-conditioning system can be obtained. By using TRNSYS simulation software on the target architecture, building cooling load can also be obtained. Based on the target building cooling load, setting the system chiller hourly load rate, establishing energy-saving and economical operation of the system of multi-objective model, and using the particle swarm algorithm to solve the model system, optimal operation parameters as thus acquired. An example: Compared with operation strategy at this stage, using the optimized operating parameters guide system operation can save 10.2% of the operating costs and reduce 15.2% of the energy losses.
在建筑能耗中,空调能耗约占建筑能耗的40%~60%左右.在夏季用电高峰期,空调用电量极大加剧了对电网的压力,冰蓄冷空调系统是在夜间制冰,在白天用电高峰期进行制冷,减少用电高峰期空调耗电量,达到“移峰填谷”的作用[1].冰蓄冷空调的使用一方面可以减小用电高峰期的电网压力,减少电厂建设的投资,达到节能降耗的作用,有利于整个社会的资源优化配置[2]; 另外,对于企业用户而言,由于存在峰谷电价,冰蓄冷空调减少了在高峰电价段的用电量,减少了用户空调的运行成本[3].冰蓄冷系统分为全负荷蓄冰系统和部分负荷冰蓄冷系统.全负荷蓄冰系统是在夜间电价低谷段蓄冰,并且第二天完全由蓄冰进行供冷,这样可以减小系统的运行费用.但是全负荷蓄冰会增加系统初投资,而且由于夜间蓄冰有一定的热量损失,较制冷机组直接供冷会消耗更多的电能耗.为了减小系统初投资和电能的消耗,所以采用部分负荷蓄冰方式.部分负荷蓄冰是在夜间电价低谷段进行蓄冰,在供冷阶段由制冷机组和蓄冰装置共同提供冷量.
关于冰蓄冷空调系统的运行,J.A. Candanedo等[4]人根据建筑负荷预测模型得到的建筑冷负荷,建立冰蓄冷空调系统经济运行模型,通过模型预测控制实现了冰蓄冷空调经济运行.Sepehr Sanaye等[5]人从能效、经济、环保等方面对冰蓄冷空调系统进行了分析; MacPhee 和Dincer[6]对不同类型的冰蓄冷空调的性能和和能效进行了研究; Y. Ma等[7],对一所大学校园的制冷系统进行模型预测控制,评估其可以节约24.5%的电力成本.国内的学者对于冰蓄冷系统运行的研究主要是为了节约用户成本使系统达到经济的效果,研究冰蓄冷空调的运行模式和制定制冰量以及蓄冰供冷的分配等运行策略.冰蓄冷中央空调系统从空调用户局部看节费不节能[8],所以,冰蓄冷空调系统运行优化的研究不能只考虑系统运行的经济性,需要找到一种使系统同时达到经济和节能效果的运行策略来,在节约用户成本的同时减少系统的能源消耗.论文通过建立冰蓄冷空调系统经济、节能的多目标模型,求解得到系统节能经济运行时制冷机组和蓄冰供冷的优化控制参数,并通过实例对比分析优化参数较目标建筑现阶段运行策略的经济性和节能效果.
冰蓄冷空调系统采取在夜间电价低谷段制冰,用于第二天电价高峰段和平价段的供冷.对于第一天夜间制冰必须保证用完,以防止“万年冰”的形成会减小融冰速率,所以确定从第一天夜间制冰开始到第二天制冰结束为冰蓄冷空调的一个运行周期.由于系统工艺要求,制冷机组设备不能反复启停,以一小时为系统的一个优化时间步长.
蓄冷空调系统是在夜间利用制冷机组提供的冷量进行蓄冰,第二天供冷阶段由制冷机组和蓄冰装置联合供冷.主要考虑冷量提供的一次侧的能耗,不考虑空气处理侧冷水循环和空气处理机组的能耗.所以系统的耗电量主要包括制冷主机的耗电量、循环液(乙二醇)泵的耗电量、冷却泵的耗电量.
(1)制冷主机的耗电量
制冷主机的耗电量主要和主机的运行荷载(实际供冷量与主机额定供冷量的比值)相关,可以根据制冷主机的实际运行数据进行二次曲线拟合[9],建立制冷主机耗电量与运行荷载的关系,而且夜间制冷主机供冷制冰和白天制冷机组直接供冷时耗电量是不一致的,所以分别建立制冰工况和供冷工况主机的耗电量与主机荷载的关系:
制冰工况:
Yi=Ai+B1Xi+C1X2i(1)
供冷工况:
Yi=A2+B2Xi+C2X2i(2)
式中:Yi为每小时耗电量,kW·h; A1,B1,C1,A2,B2,C2为拟合常数,是通过制冷机组实际的运行数据进行二次曲线拟合得到的; Xi为每小时的荷载量.
(2)循环液泵的耗电量
乙二醇循环液泵在夜间使用制冷机组蓄冰阶段和供冷阶段循环液泵都在运行,所以循环液泵的耗电量:
Esi=Psi×t1i(3)
式中:Esi为夜间蓄冰制冷机组运行时和第二天供冷阶段循环夜泵的耗电量,kW·h; Psi为乙二醇循环液泵的额定功率,kW; t1i为夜间蓄冰制冷机组运行时和第二天供冷阶段相应时间的时间步长(在夜间制冷主机运行的时间步上t1i等于1 h,制冷主机未运行时t1i等于0 h; 在第二天供冷阶段t1i等于1 h).
(3)冷却泵的耗电量
冷却泵是在制冷主机进行制冷时(包括夜间制冷蓄冰和第二天直接给建筑供冷)运行,所以,冷却泵的耗电量为:
Eci=Pci×t2i(4)
式中:Eci为制冷主机运行时冷却泵的耗电量,kW·h; Pci为冷却泵的额定功率,kW; t2i为制冷主机运行的相应时间的时间步长(制冷主机运行的时间步上t2i等于1 h,制冷主机未运行时t2i等于0 h).
(4)冰蓄冷空调系统的总能耗
在一个运行周期内,结合冰蓄冷空调系统制冷主机的耗电量、循环夜泵的耗电量、冷却泵的耗电量,冰蓄冷空调系统的能耗(总耗电量):
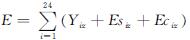 (5)
(5)
式中:E为一个运行周期冰蓄冷空调系统的总能耗(耗电量),kW·h; Yiz为系统每台冷水机组的逐时耗电量Yi之和,kW·h; Esiz为系统每台循环液泵逐时耗电量Esi之和; Eciz为系统每台冷却泵的耗电量Eci之和.
(5)系统能耗的损失率
冰蓄冷装置在夜间蓄冷,用于白天供冷.在夜间蓄冷阶段将制冷机组提供的冷量用冰的形式储存起来,白天再由制冰进行供冷,冷量会有一定的损耗.为了提高能源的使用效率,减少能源消耗,达到节能效果,定义了能耗的损失率φ:
φ=(El)/E(6)
El为利用蓄冰供冷在蓄冰和供冷过程中的能耗损失,El表示为:
 (7)
(7)
式中:c为利用蓄冰供冷在蓄冰和供冷过程中的能耗损失常数,可以根据设备使用手册和实际运行的数据确定; Tjs为夜间蓄冰时长,h.
(1)蓄冰装置模型
①蓄冰装置制冰模型
在夜间蓄冰装置利用制冷机组提供冷量进行制冰(冷水)蓄冷,建立蓄冰装置每小时蓄冷量的关系:
 (8)
(8)
式中:Bi为制冰阶段蓄冰装置每小时蓄冰的冷量,RT.H; aij为制冰工况每台制冷机组每小时的荷载率,制冰的时间段i=1,2,3,…Tjs,制冷机组台数j=1,2,3,…,n; chg为制冷机组容量,RT.H.
②蓄冰装置供冷模型
在乙二醇蓄冰系统中,蓄冷介质(水或冰)为静态,利用相变来蓄冷和释冷.系统的传热特性与热交换器类似.可以使用对数平均温差法(LMTD),得出载冷剂与冰水之间的能量平衡关系[10]:
Q=U×A×ΔTlm×10-3(9)
式中:Q为载冷剂与冰水之间的换热量,kW; U为单位面积载冷剂与冰水之间的传热系数,W/m2K; A为载冷剂与冰水之间的传热面积m2; ΔTlm为对数平均温度,K.
在盘管式蓄冰槽蓄冰供冷的过程中,随着蓄冰的融化载冷剂与冰水之间的传热面积在不断减小,因此载冷剂与冰水之间的传热面积A与冰槽中的剩余冰量有关.对数平均温度ΔTlm与冰槽进出水温度直接相关.所以,融冰供冷时的融冰速率受冰槽中剩余冰量、乙二醇溶液流量、冰槽进出水温度的影响,而冰槽中绝大部分时间进出口温度稳定,乙二醇流量也相对稳定,因此建立了融供冰冷量与冰槽剩余冰量所能提供的总冷量的关系:
bi≤g×M(10)
式中:g为待定融冰常数,根据实际运行数据确定; bi为冰槽每小时供冷量,RT.H; m为冰槽剩余冰量所能提供的总冷量,RT.H.
(2)运行周期相关约束
①冰槽蓄冰上限的约束,冰槽夜间的蓄冰量应该小于冰槽的容量:
 (11)
(11)
式中:M为蓄冰装置最大容量.
②满足室内制冷要求,由制冷机组和蓄冰提供的冷量之和应该等于建筑实时所需冷量,以满足建筑室内人员舒适度:
lli+bi=Qi(12)
 (13)
(13)
式中:Qi为目标建筑在供冷阶段逐时的所需冷量,RT.H; lli为供冷工况由制冷机组每小时提供的冷量,RT.H; chg为制冷机组容量,RT.H.aij为供冷工况每台制冷机组每小时的荷载率,i=1,2,3,…,Tgl,制冷机组台数j=1,2,3,…,n;
③融冰余量的要求,对于冰蓄冷每天运行的一个周期内,要求由夜间蓄冰设备所蓄的冷量能尽量用完,如果有剩余就会产生“万年冰”会影响蓄冰设备供冷的速率,以对融冰余量做以下约束:
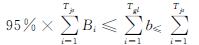 (14)
(14)
(3)冰蓄冷空调系统的运行费用
在一个运行周期内,冰蓄冷空调的总费用是系统的耗电量与相应时间步上的峰谷电价的乘积之和:
 (15)
(15)
式中:F为一个运行周期冰蓄冷空调系统的总运行费用,元; fi为目标建筑在每个时间步长上的峰谷电价,元/kW·h.
对冰蓄冷空调系统的优化设计需要在满足室内舒适度的前提下(由蓄冰和制冷机组提供的冷量等于目标建筑所蓄冷量),尽可能的减少运行费用和系统运行的能耗.
建筑的冷负荷时根据TRNSYS对目标建筑搭建模型,模拟输出建筑的负荷曲线,如图1为建筑的负荷曲线,目标建筑所蓄冷量为
Qi=∫t+Δttq(t)dt(16)
式中:Qi为目标建筑在供冷阶段逐时的所需冷量,RT.H; q(t)为目标建筑冷负荷,RT; Δt为系统的一个时间步长,1 h.
系统建立的多目标模型一方面是为了给用户减少运行成本,达到较好的经济效果,所以建立了运行费用最低的目标函数; 另一方面是为了提高能源的利用效率,减少系统能源消耗达到节能的效果,建立了系统能耗损失率最低的目标函数.建立系统经济、节能运行的多目标函数为
Minφ=(El)/E(17)
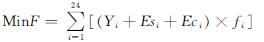 (18)
(18)
在满足室内人员热舒适度的情况下,即供冷阶段由制冷主机和蓄冰逐时提供的冷量等于目标建筑所需冷量,同时使运行费用和能耗损失率达到最小.式(10)、(11)、(12)、(13)、(14)组成系统的约束条件.
利用粒子群算法对建立的多目标模型进行求解,在系统中如果要系统运行费用降低,就需要在夜间电价低谷段尽可能多的蓄冰,但是在夜间蓄冰供冷会有一定的能耗损失,蓄的冰越多能耗的损失率越高,所以两个目标函数间具有一定的冲突关系.这就使得多目标优化问题不存在惟一的全局最优解,很难使所有目标函数同时最优.但是,可以存在这样的解:对一个或几个目标函数不可能进一步优化,而对其他目标函数不至于劣化,这样的解称之为非劣最优解(Pareto optimal)[11].
在求解模型的过程中使用了最优解评估选取的粒子群算法,对多目标优化问题的非劣最优解集的搜索算法在决策变量空间初始化一个粒子群,通过多目标优化问题中的各个目标函数来共同指导粒子在决策变量空间中的飞行,使其最终能落入非劣最优解集中.
(1)基本粒子群算法及系统变量设定
基本粒子群算法表示为,在一个n维空间中由m个粒子组成的种群,种群中第i个粒子的位置xi=(x1,x2,…,xn),其速度为vi=(vi1,vi2,…,vin),它的个体极值为gbesti=(pi1,pi2,…,pin),种群的全局极值为abest=(pz1,pz2,…,pzn).在算法设计中,每个时间步长(每小时)的a台制冷主机的荷载量为a个粒子变量.设建筑供冷时间为b小时,供冷阶段蓄冰供冷量在每个时间步长为一个变量.所以,在一个运行周期(一天)内a台制冷主机的荷载量有24a个变量; 蓄冰供冷时间为c个小时(c个变量),每个运行周期共24a+c个变量,即粒子的规模为24a+c.每个粒子的速度和位置按式(19)和(20)更新.
vij(t+1)=vij(1+1)+c1r1(t)×(gbestij(t)-xij)+c2r2(t)(zbest(t)-xij)(19)
xij(t+1)=xij(t)+vij(t+1)(20)
式中:j=1,2,…,n,i=1,2,…m,m为种群规模; t为当前进化代数; r1,r2为分布于[0,1]之间的随机数; c1,c2为加速常数.
(2)适应度函数设计
适应度表示粒子个体对环境的适应程度.这里求解的是带有约束条件的非线性规划,所以适应度函数分为针对被优化的目标函数的目标适应度和针对约束条件的约束适应度.
其中目标适应度函数为
Fmb=minF
约束适应度函数为
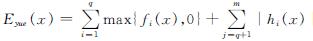
式(16)中fi(x)为约束条件中不等式约束:fi(x)≤0; hi(x)为等式约束:hi(x)=0;
(3)粒子选择规则
由于在粒子在飞行的过程中会产生不满足约束条件的解,即不可行解,在个体极值和群体极值更新时,需要比较两个离子的优劣,给定一个很小的正数ε作为约束容忍度,对产生的不可行的解采取以下规则:当Fyue(x)≤ε且Fyue(y)≤ε,即x,y都为可行解时,比较两者的目标适应度,目标适应度小的粒子为优; 当Fyue(x)≤ε且Fyue(y)ε,即x为可行解时,y为不可行解时,x粒子为优; 当Fyue(x)>ε且Fyue(y)>ε,即x,y都为不可行解时,比较两者违反约束度的程度,违反约束度较小的粒子为优.
(4)粒子群算法的步骤
①粒子群初始化:确定种群估摸N,随机产生每个粒子的位置pop(i)和速度v(i),以及种群的代数maxgen;
②用目标函数fit1(x)、fit2(x)及约束适应度函数fityue1、fityue2(x)求每个粒子的目标适应度和约束适应度,并将约束适应度最小的粒子作为群体极值zbest1、zbest2.相应的个体极值abest1(i)、gbest2(i)为粒子本身;
③利用(3)中的粒子选择规则更新群体极值abest1、zbest2;
④使用群体极值zbest和个体极值gbest(i)根据式(19)、(20)更新粒子位置,对更新后的粒子采用(3)中的粒子选择规则更新个体极值gbest1(i)、gbest2(i);
⑤为了提高粒子的全局搜索能力,利用差分演化算法对粒子进行差分变异,并对差分变异后的粒子根据(3)中的粒子选择规则更新个体极值gbest1(i)、gbest2(i)和群体极值gbest1(i)、gbest2(i);
⑥多目标函数个体极值与群体极值的评估选取
步骤一:计算两个目标函数全体极值矢量abest1、abest2的均值abest和距离dzbest;
步骤二:计算每个粒子对于两个目标的个体极值gbest1(i)和gbest2(i)之间的距离dgbest(i);
步骤三:对于每个粒子判断:如果dgbest(i)小于dzbest,则gbest(i)随机取gbest1(i)和gbest2(i)中的一个,否则best(i)取gbest1(i)和gbest2(i)的均值.
判断是否达到最大迭代次数,如果未达到则返回④,否则结束.
研究的目标建筑为西安某商场建筑,总商业建筑面积20万m2,空调面积18.76万m2,建筑物高40.6 m.制冷机组(3台)、冰蓄冷系统位于商场地下二层与地下一层.夏季商场蓄冷方式采用部分蓄 冰方式,制冷机组采用采用3台特灵CVHG1100双工况螺杆式机组(标定冷量:1 260 RT),蓄冷装置类型选了用杰美利Dyn-1300Z型冰盘管蓄冰槽蓄冷(单台冰槽蓄冷量为1 300 RT.H,共16台,总蓄冷量为20 800 RT.H).如表1所示为目标建筑峰平谷电价表.
根据式(1),使用最小二乘法进行二次曲线拟合,得到主机耗电量与主机荷载率的关系:
常规供冷:
Yi=324.1+0.091 44Xi+0.033 11X2i
制冰供冷:
Yi=353.7+0.121 67Xi+0.033 71X2i
根据目标建筑的建筑尺寸,建筑分区,人流量以及使用电器设备情况搭建目标建筑的TRNSYS模型,使用搭建的模型得出目标建筑在2015年7月18日的冷负荷曲线图.通过式(13)可以得到目标建筑在2015年7月18日建筑逐时所需冷量,如表2所示.
根据商场实际的系统,建立商场冰蓄冷空调系统运行模型,表示出系统运行费用和能耗损失率,按照式(16)、(17)建立商场冰蓄冷空调系统的经济、节能的多目标模型.通过上述的粒子群算法对模型求解可得到系统优化运行的参数(每台制冷机组逐时的荷载率).如图2是求解模型时系统运行费用和能耗损失率的寻优过程.图2中可以看出粒子群算法经过200代后,运行费用和能耗损失率的值趋于稳定,可以得到系统多目标的非劣最优解集.选取运行费用(目标1)和能耗损失率(目标2)的最优值分别是2.976万元、0.047 8.
图2 粒子群算法减小运行费用和能耗损失率的寻优过程
Fig.2 Optimization process of Particle Swarm reducing operation costs and energy loss
根据得到的系统运行费用和能耗损失率的优化结果可以得出系统制冰工况制冷机组的供冷情况和系统供冷工况下由制冷机制和蓄冰装置提供冷量的配比,其冷量的分布情况如图3所示.在粒子群变量设置中每个粒子包含了每台制冷机组逐时的荷载率,所以通过优化的结果可以对制冷机组的运行进行逐时的控制,目标建筑三台制冷机组逐时的控制参数如表3所示.
图3 系统制冰工况和供冷工况冷量分布情况
Fig.3 Capacity distribution of ice conditions and cooling system operating conditions cooling
通过图2粒子群算法的寻优过程可以看出,运行费用(目标1)和能耗损失率(目标2)具有一定的冲突关系,两个目标呈现出相反的趋势变化,经过一定的迭代次数后两个目标趋于稳定,使两个目标同时达到较优的状态.从图3系统制冰工况和供冷工况冷量分布情况可以看出当系统两个目标同时达到较优时,夜间蓄冰的冷量为19 831 RT.H,为建筑所需总冷量的30%左右,而且白天蓄冰供冷为19 786 RT.H,基本将夜间蓄冰用完.现阶段目标建筑蓄冰供冷和制冷机组的控制是根据技术人员经验性的控制,通过实际记录目标建筑在2015年7月18日实际运行费用为3.315万元的运行费用,经计算实际的能耗损失为1 753 kW·h.经过经济和节能优化后,系统运行费用为2.976万元,损失能耗为1 486.5 kW·h.所以,经过经济优化的结果可以为用户节约10.2%的运行费用,并可以减少15.2%能耗损失.
论文通过建立冰蓄冷空调系统的运行模型,得到系统运行周期内的运行费用和运行能耗.并通过对目标建筑的TRNSYS建模,模拟得出冰蓄冷空调运行周期内的冷负荷.依据目标建筑冷负荷,建立了冰蓄冷空调系统运行费用和能耗损失率最低的多目标模型.使用改进的粒子群算法求解模型,得到运行周期内制冷机组的逐时荷载率,以及供冷阶段蓄冰供冷和制冷机组供冷的配比.通过实例分析,结果表明:
(1)目标建筑蓄冰供冷和制冷机组的控制是根据人员经验性的控制,系统的运行未能达到较好的经济、节能效果.
(2)通过建立系统的经济、节能的多目标模型,求得的制冷机组的控制参数以及制冷机组和蓄冰装置供冷的配比可以为用户节约10.2%的运行费用,并可以以减少15.2%能耗损失.
(3)通过对冰蓄冷空调的优化控制,可以提高系统给用户带来的经济效益,并可以达到节能减排的效果,对冰蓄冷空调的推广使用具有促进作用,从而可以减少电站的投资和电网的负荷压力.