基金项目:国家自然科学基金(51338004; 51178175)
第一作者:易伟建(1954-),男,博士,教授,博士生导师,主要从事混凝土的基本理论研究.E-mail: wjy@hnu.edu.cn
(School of Civil Engineering, Hunan University, Changsha 410082, China)
eccentrically capacity of punching shear; ultimate strength analysis; slab-column connections; Mohr-Coulomb Criterion
DOI: 10.15986/j.1006-7930.2018.02.002
将轴向力和弯矩共同作用下的板柱节点冲切转化为一个偏心作用力效应,基于塑性极限分析的方法,提出平动-旋转复合运动机构模型分析节点的偏心冲切,推演求出了偏载作用下的承载力的泛函表达式; 通过构造的破坏曲面近似求出了节点在偏载作用下的抗冲切承载力的最小值,对计算结果进行了简化拟合,并与规范和其他的计算方法进行了比较; 试验数据分析表明:平动-旋转复合运动机构模型相比与偏心剪应力模型能更好的反应柱子尺寸与板厚的比值对承载力的影响,并基于试验数据对公式进行了部分调整,计算结果与试验结果吻合良好.
The plate under the action of axial force and moment punching problem is transformed into a node eccentric force effect, Based on the plastic limit analysis method, the translational-rotational compound motion mechanism model is proposed to analyze the ultimate bearing capacity of slab -column connections, and the functional is deduced. The proximate bearing capacity under partial load was calcu lated with the assumed yield surface. Furthermore, the results were appropriately simplified, and the calculation method proposed in this paper and other calculation methods introduced in our existing specification are compared and evaluated. The comparison of the calculation methods shows that the composite motion mechanism model can reflect the influence of the ratio of column to plate thickness on the bearing capacity more accurately than the eccentric shear stress model. The adjusted method proposed in this paper is accurate to fit the test results well.
钢筋混凝土板柱结构是一种只由楼板和柱组成的结构体系,这种结构有施工简便、空间利用率高、布局灵活等诸多优点,在停车场、住宅、仓库等建筑中有着广泛的应用.但是,板柱结构的节点容易发生脆性冲切破坏,而且一个节点的冲切破坏可能引起相邻节点因过载而相继破坏,进而引发结构连续倒塌.
对板柱节点抗冲切性能研究已有近百年的历史,并积累了相当丰富的试验数据[1].特别是中柱节点在轴向荷载下受力性能的研究较为充分.现有的研究表明:板柱节点在不平衡弯矩地作用下其抗冲切承载力会有所下降,而板柱结构在承受竖向荷载的同时由于重力荷载的偏心,横向风作用以及地震作用不可避免地会产生不平衡弯矩,进而降低节点的承载力.不平衡弯矩下的冲切破坏机理较为复杂,相关的研究也相对较少,我国混凝土结构设计规范也仅在附录中列出了计算公式[2].
国内外学者提出了一些板柱节点在不平衡弯矩作用下冲切承载力的计算方法或计算模型,如:1976年Islam和Park在屈服线理论地基础上采用拟梁法建立了节点的承载力的计算公式[3-4]; 1981年Dilger等人在低周反复荷载试验的基础上运用屈服线理论得到了不平衡弯矩作用下的荷载计算公式[5]; 我国的马元昌、吕西林于2001年在抗弯塑性铰理论的基础上进行极限分析得到了抗弯和抗剪相关方程的联合计算公式[6]; 2007年Ying Tian基于试验研究和历史数据库提出以拟梁法为基础的计算模型[7]; 2013年洪小滔研究了混凝土强度、冲垮比、配筋率对偏载下板柱节点冲切强度的影响[8]; 2014年Choi等人基于临界截面应变分布提出考虑不平衡弯矩作用下的计算模型[9].
在板柱节点抗冲切承载力的塑性极限分析方面,也取得相关的研究成果.1976年Braestrup等利用修正的Mohr-Coulomb理论求解出了轴对称冲切问题的最小上限解[10]; 1986年蒋大骅等采用抛物线形的Mohr-Coulomb屈服准则,使得圆柱节点的最小上限解的表达式更为简洁[11].1993年周朝阳在采用塑性分析方法研究板柱节点冲切承载力时提出考虑斜截面面内的旋转的错动-转动复合机构[12],相比于传统的错动模型能考虑径向和环向配筋的影响; 2002年,Salim W, Sebastian W M在蒋大骅的基础上对极限分析做了一些修正[13],2017年易伟建、刘彪提出基于塑性理论的钢筋混凝土板冲切开裂滑移模型[14].
对于轴对称的板柱节点塑性极限分析,Braestrup等利用修正的Mohr-Coulomb破坏准则[10],蒋大骅等采用抛物线型的Mohr-Coulomb破坏准则[11],严宗达等采用双剪强度理论[15],魏雪英等采用统一强度理论[16].抛物线型Mohr-Coulomb破坏准则能较好的反映混凝土在较大正应力作用下剪力并非与正应力成比例增加的现象,并且连续可导,便于运算.本文采用文献[11] 给出的抛物线形Mohr-Coulomb准则:
(σn)/(f't)+1/K((τnt)/(2f't))2=1(1)
m=(f'c)/(f't)=(vvfc)/(vtft)(2)
K=1/4[m+2(1-(m+1)1/2)](3)
其中:f't和f'c分别为混凝土的有效抗拉和抗压强度,ft和fc分别为混凝土的抗拉和抗压强度,vt和vc为相应的有效系数.
根据图1可以求出抛物线外法线与τn轴夹角α与应力之间的关系为
tanα=-(dτnt)/(dσn)(4)
结合式(1)可以得到:
tanα=2K(f't)/(τnt)(5)
则应力与夹角的关系为
 (6)
(6)
将上式应力代入到应力圆中,可以求得其主应力.
 (7)
(7)
以及切向正应力:
σt=[1-K(cscα+3)2]f't(8)
对板柱节点的冲切破坏进行塑性极限分析时,将柱头与未屈服区域的板视为刚体,外力作用下柱头(冲切破坏锥)与板之间形成屈服面,达到塑性极限状态.当没有不平衡弯矩时,柱头整体可能的运动机构只会发生向下平动.当存在不平衡弯矩时,与轴向力和不平衡弯矩相对应,柱头整体在平动的同时还会发生转动,按图2所示的运动机构,可计算轴力和不平衡弯矩所做的功.
将轴向力和弯矩共同作用转化为一个偏心作用力,节点在偏载作用下发生冲切破坏.此机构分为三部分,不动刚体Ⅰ,运动的柱头刚体Ⅱ以及塑性屈服区域Ⅲ,屈服域的厚度为δ.运动的柱头刚体Ⅱ绕着点R(x0,z0)产生角速度为ω的旋转运动.柱的中心轴线的运动可分解为一个沿z轴的平动-ωx0,和一个角速度为ω的旋转运动,将这种运动机构称为平动-转动复合运动机构.现假设破坏锥体屈服域为如图2所示坐标中的一待求函数,可以在直角坐标表示为
z=g(x,y)(9)
在本文中g'x、g″xx分别表示函数g对x一阶和二阶偏导.
e0=(Munb)/P(10)在图2所示的平动-转动复合运动机构下,锥体屈服域上任意一点的竖直方向的速率为u,水平方向的速率为v,正方向如图2所示,则可求得运动速率:
 (11)
(11)
屈服面上沿Y轴方向的运动速率为零,现假设屈服域的形状函数能满足:
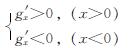 (12)
(12)
则将运动速率分解为向屈服域的法线方向和切面上可以求得应变速率:
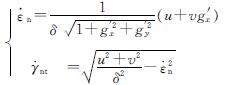 (13)
(13)
塑性增量理论的假设为:在塑性变形过程中的任一微小时间增量内,瞬时应力偏量与应变增量成比例,即:
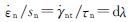 (14)
(14)
式中,dλ为一与路径有关的非负标量.
应力偏量:
sn=σn-(σ1+σ3)/2=2K(15)
结合式(6)、(14)可以得:
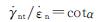 (16)
(16)
由式(14)、(15)得:
 (17)
(17)
可得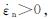 现将式(16)代入式(6)屈服面上的应力可以表示为
现将式(16)代入式(6)屈服面上的应力可以表示为
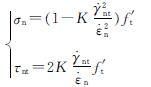 (18)
(18)
在屈服域上存在应力σn τn应变速率 做功,所以单位面积的屈服面内力做虚功为
做功,所以单位面积的屈服面内力做虚功为
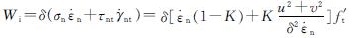 (19)
(19)
屈服域的面积为
ds=(1+g'2x+g'2y)1/2dxdy(20)
屈服域做的总内虚功:
WI=∫ds∫Wids(21)
联立式(13)、(20)、(21)可以求得屈服域内力做的总内虚功为
WI=∫Dxy∫[(u+vg'x)(1-K)+K(u2+v2)/(u+vg'x)(1+g'2x+g'2y)]f'tdxdy(22)
外力做的虚功为
WE=P(e0-x0)ω(23)
根据外力和内力虚功相等的原则,则有:
WE=WI(24)
所以可以求得承载力:
∫Dxy∫(f'c)/(m(e0-x0))[[(x-x0)+(g-z0)g'x](1-K)+K((x-x0)2+(g-z0)2)/((x-x0)+(g-z0)g'x)(1+g'2x+g'2y)]dxdy(25)
承载力P为一泛函数,现在确定函数P的边界条件,即屈服面在xy平面的投影,积分区域D的边界条件Г由边界Г1和边界Г2两部分组成,对于板的冲切问题上边界Г1一般认为是沿着柱边破坏的,即柱子的形状边界函数,是固定的; 而对于板的下边界Г2未知的,即边界Г2为可变边界.在特定机构下的最小承载问题转化为对含有一个可变边界条件泛函数P的极值问题,对于这类含有多元函数的泛函数的可进行变分求解.现令:
F=(f'c)/(m(e0-x0))[[(x-x0)+(g-z0)g'x](1+K)+K((x-x0)2+(g-z0)2)/((x-x0)+(g-z0)g'x)(1+g'2x+g'2y)](26)
根据文献[17]泛函数取得极值的必要条件是要求满足欧拉方程:
 (27)
(27)
同时,补充在可变边界条件上,得:
 (28)
(28)
对于一般的情况,要直接求出解析解存在一定的困难.现考虑没有不平衡弯矩作用时的特殊情况.当偏心距为零时柱的轴线不发生转动,只有平动运动,得:
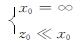 >(29)
>(29)
对于这种特殊的情况,式(25)简化为
P[g(x,y)]=∫Dxy∫(f'c)/m[1+K(1+g'2x+g'2y)]dxdy(30)
同时,式(26)简化为
F=(f'c)/m[1+K(g'2x+g'2y)](31)
代入欧拉方程(27)得:
g″xx+g″yy=0(32)
得出的结论与文献[18]一致,即文献[18]所求出的结论只是本文的一种特殊情况.若对于圆柱板轴对称问题可以对调和方程做一个柱坐标变换,同时代入边界条件Г1、Г2则可以求出圆柱板的冲切解析解.
现在假设板上表面沿着柱边破坏,下表面破坏边缘距离柱中心的距离为d1/2,屈服面g函数的边界条件Г1、Г2为
 (33)
(33)
求得:
Pe0=0=(2πf'c)/m((d21-d2)/2+(Kh2)/(lnd1-lnd))(34)
当:
 (35)
(35)
可以取得最小值,计算结果与文献[11] 一致.
对于最小上限解,当求解析解存在一定困难时,可以采用类似于构造形函数的方法求近似解,当构造的曲面函数合适时求出的最小解与解析解通常误差会很小.所以本文拟采用构造形函数的方法近似求解,对计算结果进行分析得出实用的结论.
为便于分析对上文坐标转换为柱坐标体系,根据坐标变换公式:
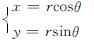 (36)
(36)
得到:
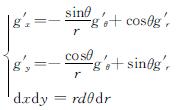 (37)
(37)
所以求得承载力:
P=∫Drθ∫(f'c)/(m(e0-x0))[A(1-K)+KB/A(r2+r2g'2r+g'2θ)]drdθ(38)
上式中:
 (39)
(39)
文献[8]一共进行了8块板在偏载作用下的冲切试验(如图3),根据实验现象表明破坏曲面在远离偏载侧的冲切锥一般要略为平缓一些,同时曲面下凸,对于r是单调,所以可以根据这些实验现象构造屈服面函数.
图3 偏载下典型的冲切破坏面[8]
Fig.3 Typical failure surface under eccentric load
如图4现在拟定屈服面g函数的边界条件Г1、Г2为
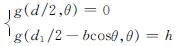 (40)
(40)
边界条件Г1沿柱边,为固定边界条件; 边界条件Г2中d1,b为待定量,为可变边界条件.现假设曲面函数g沿在同一角度θ处为满足边界条件Г1、Г2二次多项式的曲线.根据这些假设可以构造曲面函数:
g(r,θ)=[((2r-d))/((1-a)(d1-2bcosθ-d))-(a(2r-d)2)/((1-a)(d1-2bcosθ-d)2)]h(41)
式中,a为二次多项式待定参数,当a=0时,破坏面退化成圆台.
将式(41)代入(38)即可求得承载力P,为求得所有可以发生的运动机构中的P的最小值,可以设计计算方法寻找P的最小值.
现在未定量为边界条件变量d1、b,曲面二次多项式参数a,和旋转中心R0(x0,z0)四个待定量.所以本文在确定相关参数的取值范围后采用多重搜索的方法求出P的最小值.根据试验现象一般可以大致确定一些参数的取值范围.边界条件中,d+h<d1<d+10h,0≤b<h; 二次多项式参数:0≤a<0.5; 旋转中心参数:x0≤0.
现取m=100[13, 18],通过数值计算的方法可以求出式(38)的在偏载下的承载力,通过多重搜索可以找出承载力的最小值,其最小承载力与非偏载下的理论值式(34)中Pe0=0的比值如图5中的点标所示.可见承载力主要与参数d/h,e0/(d+h)有关.为应用方便,对计算的结果采用参数d/h、e0/(d+h)的多项式进行拟合,图5中的线标为式(42),可见拟合的公式与直接计算的结果是比较接近的.
P=(Pe0=0)/(1+(e0)/(d+h)[0.15((e0)/(d+h))1/3+0.425](d/h)1/3)(42)
在工程应用中板的厚度一般采用有效厚度h0,为保持一致,本文的计算方法中h视为板的有效厚度,e0=Munb/Pe0为偏心距.在计算方柱时采用等效圆柱直径,根据面积等效的原则, d=1.13c.轴对称条件下的承载力计算采用文献[18]的公式:
Pe0=0=0.84(h0/c)1/6(100ρ)1/2f1/3cumh0(43)
式中,um同为距离柱边h0的周长,根据式(42)可以得到偏心作用下的冲切承载力.
我国规范[2]对于非预应力板在不配置箍筋或弯起钢筋时在集中反力作用下或者局部荷载的冲切承载力Fl计算应该满足式(44),相关参数的含义详见规范[2].
Fl≤0.7βhftηumh0(44)
在偏心作用下,采用等效集中反力设计:
Fl,eq=Fl+(α0MunbαAB)/(Ic)umh0(45)
对于方柱截面边长为c中间板柱节点,代入相关公式,令其e0=Munb/Fl,可以计算得:
Fl,eq=Fl(1+1.2(e0)/(c+h0))(46)
式(46)的等效集中荷载Fl,eq应满足式(44),得到在偏载作用下的承载力计算公式:
Fe0=Fl=(0.7βhftηumh0)/(1+1.2(e0)/(c+h0))(47)
文献[19]对规范公式进行了修正,给出了中柱节点在Vg和不平衡弯矩Munb联合作用下的半经验半理论承载力公式,对于柱尺寸为c的方柱,其计算化简后如下
(Vg)/(F0)=1/(1+1.2(e0)/(c+h0))(48)
F0=ξftumh0(49)
ξ=1.4ρfy/(ff+ρfy)(50)
式中:F0为板柱节点在没有不平衡弯矩作用下的冲切承载力,e0=Munb/Vg为等效偏心距,ft为是混凝土轴心抗拉强度,fy是纵向钢筋屈服强度值 c是方柱的边长,h0为板的效高度,um为截面临界周长.
所以在偏载作用下的承载力为
Vg=F0/(1+1.2(e0)/(c+h0))(51)
现在对文献[19]公式、我国现行规范考虑的偏心作用与本文的极限分析计算的结果进行对比如图6所示,文献[19]公式和规范对中柱方形柱的偏心作用下的折减效应是一致的.
由图6可知,本文的极限分析计算的偏心对承载力的影响的折减效应比规范和文献[19]公式偏小,这可能是由于在偏载作用下所假设的曲面与理论的曲面存在偏差导致承载力偏高或者是由于混凝土并非理想的弹塑性材料,在复杂的偏心受力状态下承载力相对于规范或其他基于试验统计得出的经验公式的折减效应偏小.在等效偏心距的坐标下,规范和文献[19]公式对于中间方柱板都没有考虑柱尺寸和板厚度的比值对载力折减效应的影响,而本文的极限分析结果表明柱尺寸和板厚度的比值对折减效应有着较大的影响.
文献[20]整理了一共39个试验数据,适用于本文公式计算的有效数据一共36个,对其试验值承载力和计算承载力的比值在c/h0的坐标下所示,图中虚线为回归线.
由图7可知,规范GB50010-2010和文献[19]公式对于c/h0的影响趋势都不太准确,而本文的极限分析的结果对c/h0的影响的趋势预测相对更为准确,但极限分析计算得出的节点的承载力整体偏高,基于试验数据对本文的极限分析的结果进行调整,调整后的计算公式如下:
P=(Pe0=0)/(1+(e0)/(d+h0)[0.15((e0)/(d+h0))1/3+0.8](d/(h0))1/3)(52)
调整后的计算值与试验的对比如图8.
此时平均值为1.028,变异系数为0.144,离散性以及对柱宽与板厚比值影响趋势都明显优于规范GB50010-2010和文献[19].
当采用附加剪力表示弯矩对冲切承载力的不利影响时,将板柱节点的等效剪力设计值表示为
Fl,eq=Fl+(Fle0)/(d+h0)[0.15((e0)/(d+h0))1/3+0.8](d/(h0))1/3(53)
式中:Fl,eg为等效剪力设计值,应小于非偏心冲切下的承载力的值; Fl为重力荷载设计值,e0=Munb/Fl为偏心距; h0为板的有效厚度; d为柱的直径,为方柱时取为1.13倍的方柱边长.此计算公式适用于存在不平衡弯矩的中柱板柱节点冲切承载力计算.
(1)采用塑性极限分析方法,针对圆柱形板柱节点在轴向力和弯矩共同作用的受力条件,提出平动-旋转复合运动机构,通过推演得到板柱节点抗冲切承载力的上限解,物理含义明确.
(2)求出了求解上限解的方法,为简化计算,通过构造的破坏曲面,采用数值算法求出了节点在偏载作用下的承载力,对计算结果进行了简化,并与规范和其他的计算方法进行了比较,试验数据表明平动-旋转复合运动机构模型相比与偏心剪应力模型能更准确的反映柱子与板厚的比值对承载力的趋势影响.
(3)根据试验数据对计算公式进行了修正调整,调整后的计算公式与试验结果吻合良好,明显的优于规范及其它计算公式,可用于实际工程设计.
(4)由于收集的试验数据有限,方柱板边长与板厚度比值的影响还有待于更进一步的研究.