基金项目:“十二五”国家科技支撑计划(2011BAJ09B01-01); 贵州省科技合作计划项目(黔科合LH字[2016]7468号)
第一作者:姜 岚(1986-),男,博士生,讲师,主要从事空间网格结构方面的研究工作.E-mail:jianglanctgu@163.com 通信作者:马克俭(1933-),男,中国工程院院士,教授,博士生导师,主要从事空间结构的研究与应用工作. E-mail:makejian2002@163.com
(1.湖南大学 土木工程学院,湖南 长沙 410012; 2.贵州大学 空间结构研究中心,贵州 贵阳 550025; 3.三峡大学 电气与新能源学院,湖北 宜昌 443002)
(1.School of Civil Engineering, Hunan University, Changsha 410012, China; 2.Space Structure Research Center, Guizhou University, Guiyang 550025,China; 3.College of Electrical engineering and New Energy, China Three Gorges University, Yichang 443002,China)
Shear Connector; vierendeel beam; simplified calculation method; vierendeel sandwich plate
DOI: 10.15986j.1006-7930.2018.03.007
基于费氏空腹桁架理论,建立了剪力键式钢空腹梁内力及变形简化计算方法.通过精细化有限元方法分析了三种不同节点形式剪力键式空腹梁的内力及变形分布规律、影响因素,并与简化计算方法进行对比.分析表明:设置加劲肋可以显著改善空腹梁的内力及变形特征; 挠度简化计算方法能准确反映设置加劲肋的空腹梁变形特征; 修正后的应力计算方法可以用于工程实践.
This paper presents a new simplified calculation method. The method is based on the theory of Allftlish vierendeel truss. Analyzes the internal force and Deformation of vierendeel beam with three kinds of connections. Compare the value calculated by finite element method and by simplified calculation method. The analysis shows that the ribbed stiffener is important to internal force and deformation of vierendeel beam. The revised simplified calculation method can convey accurate signals of internal force and deformation.
剪力键式钢空腹梁由型钢上肋、型钢下肋及方管剪力键组成,是借鉴木结构中“离缝式”组合梁[1]发明的一种新型钢空腹梁[2].剪力键式钢空腹梁是钢空腹夹层板楼盖体系的基本构件,具有跨高比大、结构高度小、用钢量省、节省层高的优点.该结构形式适合应用于大跨度多层工业与公共建筑以及“大开间灵活划分”的住宅与商业建筑,目前已经应用于多项试点工程,取得了较好的经济与社会效益.马克俭团队从2000年开始致力于剪力键式钢空腹楼盖的研究与推广,积累了丰富的工程实践经验并提出了实用计算方法[2-3].
在空腹夹层板的刚度计算方面,张定华等[4]将空腹夹层板等效为实腹交叉梁系并采用能量法提出了结构的竖向挠度方程.黄勇等[5]根据Reissner型夹层板理论推导了剪力键式空腹夹层板的连续化六阶偏微分方程.张华刚等[6]从工程实践出发,为考虑空腹夹层板剪切变形、混凝土二次浇筑以及收缩和徐变等不利因素的影响,将刚度等效交叉梁系的最大弹性挠度除以0.65作为空腹夹层板整体挠度的控制值.目前在钢空腹板的设计中,上、下肋一般采用T型钢或H型钢,剪力键一般采用方钢管.计算挠度时多采用估算法或精细化有限元法.估算法对设计经验要求较高,精细化有限元法建模及分析过程繁琐,不适用于工程设计.本文在以上研究的基础上,根据剪力键式钢空腹梁的结构特点,分析其变形特征,提出一种基于费氏桁架理论的应力及变形简化计算方法,并与精细化有限元计算进行对比,验证其实用性.
基于费氏空腹桁架理论,以上、下肋为T型钢截面的剪力键式空腹梁为例,简化分析模型.基本假定如下:
(1)剪力键式空腹梁受弯时,梁截面保持平面变形;
(2)上、下型钢肋的的反弯点位于网格中央.
以受均布荷载作用的简支空腹梁为例分析剪力键式空腹梁受弯正应力简化计算方法.首先按抗弯刚度EI等效原则,将上、下肋为T型钢的剪力键式空腹梁等效为H型钢实腹梁.如图3所示,等效后保持截面总体高度h不变,翼缘宽度bT及厚度tT不变,则等效腹板厚度可按式(1)计算:
th=tw[1-(1-(2hT)/h)3](1)简支等效梁在均布荷载q作用下的弯矩为M,剪力为V.则1-1截面的正应力可按式(2)计算:
σ1=M/(Wn)(2)
图3中第i个网格2-2截面和3-3截面的应力包含弯矩M引起的正应力和剪力V产生局部弯矩应力两部分,故可按式(3)计算:
σ2=σM+σV=M/(Wn)±(Via)/(4WT)(3)
式中:M为等效梁对应空腹梁计算位置的的弯矩,qx2/2; 总体弯矩下的正应力; σM为剪力引起局部弯矩下的正应力; σV为等效梁对应空腹梁第i个网格中心点位置的剪力,i≤n/2; a为网格尺寸; Wn为空腹梁截面抵抗矩; WT为上(下)肋T型截面抵抗矩.
式(3)中的正负号由局部弯矩的方向决定,如2-2截面应力计算取“+”号,3-3截面正应力计算取“-”号.空腹梁各截面正应力分布如图4所示.2-2截面和3-3截面组合应力分布与σM、σV相对大小有关.边网格与中部网格各截面应力分布如图4(b)、图4(c)所示.
根据费氏空腹桁架基本假定,可取图5(a)所示受力单元,根据力平衡条件:
T=(a(Vi+Vi+1))/(2z)(4)式中:T为剪力键剪力; Vi+1等效梁对应空腹梁第i+1个网格中心点位置的剪力,i≤n/2; z为上、下肋截面形心之间的距离.
剪力键、上(下)肋剪应力分别为
τ1=(TS·)/(t0Iz)(5)
τ2=(VST)/(2tWIT)(6)
其中:τ1为剪力键剪应力; S·为剪力键距中性轴为y的横线以外的横截面积对中性轴的静矩; Iz为对截面中性轴的惯性矩; τ2为上(下)肋剪应力; ST为上(下)肋距中性轴为y的横线以外的横截面积对中性轴的静矩; V为等效梁对应空腹梁计算部位的剪力; IT肋截面惯性矩.
根据抗弯刚度与截面面积等效原则,将剪力键式钢空腹梁等效为实腹梁.基本假定如下:
(1)剪力键线刚度远远大于上、下肋线刚度,即不考虑剪力键变形对总体挠度的影响;
(2)忽略剪力键轴向内力作用.
在跨高比较大的实腹型钢梁中,荷载作用下的挠度以弯矩挠度为主,剪切变形极小可以忽略.在剪力键式钢空腹梁中,由于相邻剪力键与上、下肋之间形成空腹,因此剪力引起的挠曲变形不可忽略.
剪力键式钢空腹梁的竖向挠度组成可表示为
f=fM+fV+fJM(7)
其中:f为总的挠度; fM为弯矩引起的挠度; fV剪力引起的挠度; fJM肋局部弯矩引起的挠度.
剪力与局部弯矩引起的挠度在总的挠度中所占的比重与空腹梁跨高比、网格大小、肋的刚度相关.
均布荷载q作用下的弯曲挠度计算:
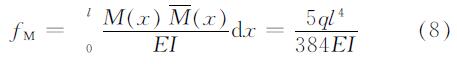
式中:q为空腹梁上均布荷载; E为材料弹性模量; I为等效梁截面惯性矩.肋剪切挠度fV计算:
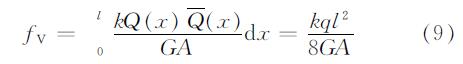
式中:k为受剪截面形状系数,按A/A1(A1为腹板面积)计算; G为剪切弹性模量; A为空腹梁受剪截面面积.
第i个网格肋中央的剪力将会在肋中产生局部弯矩M0,M0产生的局部弯曲挠度fJM可按下式计算:
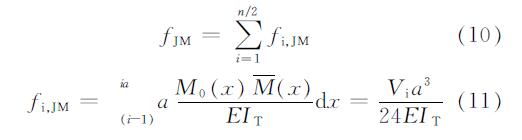
式中:Vi为等效实腹梁在第i个网格中心点处的剪力; a为网格尺寸; IT为上(下)肋截面惯性矩.
相关研究表明[7],采用有限元方法分析钢结构内力及变形与试验结果吻合较好.根据剪力键式钢空腹梁的结构特点,本文采用壳单元模拟上、下肋及剪力键,构建空腹梁有限元计算模型.空腹梁跨度L为12 m,计算边界条件为梁端简支,荷载为5 kN/m线荷载.通过观测了解剪力键式空腹梁的应力分布及变形特点.分析跨高比、网格尺寸、加劲肋尺寸对空腹梁内力、变形的影响,并验证简化计算方法的可行性.
在简化计算中,将剪力键节点视为刚性节点.然而在实际工程中,存在不同的节点构造措施[8].节点构造处理对节点刚度及应力分布有一定影响.本文参照目前钢空腹夹层板的应用情况,设计了三种剪力键节点,如图6所示.分析三种节点形式对空腹梁应力及变形的影响.
三种节点形式下的空腹梁应力分布基本一致.本文以B型节点空腹梁为例说明应力分布特点(图7所示).空腹梁各部位横截面应力分布如图8所示.
从图7、图8可见,剪力键式空腹梁应力分布存在如下特征:①梁端网格靠近节点处截面T型肋腹板应力起控制作用,肋中部截面翼缘应力起控制作用,表明空腹梁端部网格局部弯矩作用效应比轴向力作用效应显著.②空腹梁中部网格的翼缘应力起控制作用,表明跨中网格轴力作用效应比局部弯矩作用效应显著.③边网格内空腹处腹板与剪力键连接部位存在显著的应力集中现象,整个空腹梁的截面应力由端部网格节点处截面控制.三种节点剪力键式空腹梁最大应力如表1所示.从表1可以看出,三种节点空腹梁有限元计算结果显著大于简化计算结果,均存在应力集中现象.三种节点形式节点处应力集中程度不同,A型节点应力集中效应最显著,B型节点次之,C型节点应力集中程度最弱.
相比B型节点和C型节点,A型节点局部变形显著,表现为受压腹板将剪力键压至内凹,受压腹板将剪力键拉至外凸(图9),与试验结果一致[9].三种节点空腹梁竖向最大挠度如表2所示.
从表2可以看出,B、C型节点空腹梁最大挠度与简化计算方法接近,表明简化计算方法计算挠度具有较高的精确度.A型节点空腹梁挠度与B、C节点空腹梁挠度相差较大,其原因在于剪力键局部变形导致上(下)肋刚体转动产生累计附加挠度.在结构分析时,A型节点不满足刚性连接假定,具有显著的半刚性特征,对于其刚度系数,需进一步深入研究.B、C型节点可视为刚性节点.将空腹梁跨度与横截面总高度之比定义为跨高比.空腹夹层板的跨高比通常在18~26之间[10].空腹梁跨高比在此范围内取值.空腹梁跨度为12 m,网格尺寸为2 m.T型钢截面宽度200 mm,高度150 mm,翼缘厚度10 mm,腹板厚度10 mm.剪力键宽度200 mm,厚度12 mm.
三种节点形式空腹梁有限元计算最大应力与简化计算方法最大应力随跨高比变化趋势如图 10(a)所示,挠度值随跨高比变化趋势如图 11(b)所示.
由图 10(a)可见:①A型节点空腹梁应力水平显著大于B、C型节点.②简化计算方法计算的最大应力显著小于有限元方法计算值.需对简化计算值进行修正.③有限元计算值与简化计算值均随跨高比呈线性变化,且斜率较小,表明跨高比对最大应力影响不显著.由图 10(b)可见:①B、C节点形式空腹梁挠度有限元计算值略小于简化计算值,表明简化计算方法可以较为准确地计算B、C型节点空腹梁挠度.②A型节点空腹梁挠度有限元计算值与简化计算值误差较大,不宜采用简化计算方法计算该种节点空腹梁挠度.③跨高比对挠度影响显著.
网格尺寸为空腹梁两相邻剪力键中心点之间的距离.考虑到混凝土面板的经济性,空腹夹层板的网格尺寸一般在1.4~2.6 m之间.空腹梁网格尺寸在此范围内取值.空腹梁跨度为12 m,总高度0.6 m.T型钢截面宽度200 mm,高度150 mm,翼缘厚度10 mm,腹板厚度10 mm.剪力键宽度200 mm,厚度12 mm.
三种节点形式空腹梁有限元计算最大应力与简化计算方法最大应力随网格尺寸变化趋势如图 11(a)所示,挠度值随网格尺寸变化趋势如图 11(b)所示.
由图 11(a)可见:①网格尺寸对最大应力影响较为显著; ②最大应力有限元计算值均大于简化计算值; ③设置加劲肋的两种节点形式空腹梁的最大应力值接近,不设置加劲肋的空腹梁应力计算值大于设置加劲肋的应力值.由图 11(b)可见:①网格尺寸对挠度的影响程度较小; ②挠度简化计算值与B、C两种节点形式的有限元计算值较为接近,且略大于有限元计算值; ③A型节点空腹梁挠度有限元计算值远大于简化计算值.
将空腹梁空腹部分高度占空腹梁总高度的百分率定义为空腹率(h-2hT)/h.空腹夹层板的空腹率一般在30%~70%之间.空腹梁跨度为12 m,总高度0.6 m,网格尺寸为2 m.T型钢截面宽度200 mm,翼缘厚度10 mm,腹板厚度10 mm.剪力键宽度200 mm,厚度12 mm.
三种节点形式空腹梁有限元计算最大应力与简化计算方法最大应力随空腹率变化趋势如图 12(a)所示,挠度值随网格尺寸变化趋势如图 12(b)所示.
由图 12(a)可知:①空腹率对空腹梁最大应力影响较大,随着空腹率的增大,最大应力呈指数式增长,并超出材料的弹性范围; ② A型节点应力最大,B、C型节点应力相当,计算计算结果最小.由图 12(b)可知:①空腹率对空腹梁挠度影响较大,随着空腹率的增大,最大挠度呈指数式增长; ②简化计算挠度值略大于B、C节点有限元计算挠度值; ③A型节点空腹梁挠度有限元计算值与简化计算值差别较大.
由以上分析可知:①在常规设计参数范围内,挠度简化计算方法计算值与有限元计算值吻合较好,可直接用于剪力键式空腹梁变形计算; ②最大应力简化计算值由于未考虑应力集中效应,要小于有限元计算值,应对其进行修正.
通过在式(3)中引入应力集中效应系数φ最大正应力进行修正,即
σ'2=φ σ2(12)
对最大应力影响较显著的因素为网格尺寸和空腹率.通常情况下,空腹夹层板空腹梁的空腹率在30%~70%之间,网格尺寸在1.5~2.4 m之间.控制空腹梁跨度12 m,总高度0.6 m,T型钢截面宽度200 mm翼缘厚度10 mm,腹板厚度10 mm,剪力键宽度200 mm厚度12 mm不变,改变空腹率及网格尺寸,进行有限元参数化分析,获得φ值影响曲线,如图 13所示.
有图 13可知:①应力集中效应系数随着空腹率及网格尺寸的增大呈增大趋势; ②A型节点空腹梁的应力集中效应系数主要分布在3~4之间,B、C型节点空腹梁的应力集中效应系数主要分布在2~3之间; ③为保守起见,A型节点空腹梁可取φ=4,B、C型节点空腹梁可取φ=3.(1)无加劲剪力键式空腹梁的应力集中十分显著,且节点存在显著的半刚性特征,不宜直接应用于工程.通过在剪力键式空腹梁节点处布置竖向或水平加劲肋,可显著减小剪力键局部变形,并显著降低应力集中效应.
(2)应力简化计算公式能较好地反映剪力键式空腹梁各部位应力分布规律与趋势,但不能反映应力集中效应,可通过应力集中效应系数进行修正.
(3)挠度简化计算公式计算得到的挠度值与设置加劲肋的空腹梁有限元计算挠度值吻合良好,总体误差在10%以内,且偏于保守,可用于工程实践.