基金项目:国家自然科学基金项目(51378068,51778058); 陕西省自然科学基金项目(2018JQ5219); 青海省交通科技项目(2017-咨13)
第一作者:程 高(1988-),男,博士,工程师,研究方向为钢桥与组合结构桥梁.E-mail:1255726999@qq.com 通讯作者:刘永健(1966-),男,博士,教授,研究方向为钢桥与组合结构桥梁.E-mail:lyj.chd@gmail.com
(1.长安大学 公路学院,陕西 西安 710064; 2.西北农林科技大学 水利与建筑工程学院,陕西 杨凌 712100; 3.长安大学 桥梁与隧道陕西省重点实验室,陕西 西安 710064)
(1.School of Highway, Chang'an University,Xi'an 710064, China;2. College of Water Resources and Architectural Engineering, Northwest A&F University, Yangling 712100,China;3. Key Laboratory for Highway Bridge and Tunnel of Shaanxi Province, Chang'an University, Xi'an 710064, China)
concrete-filled steel tube; rectangular; longitudinal stiffener; local buckling; analytical solution; design
DOI: 10.15986j.1006-7930.2018.04.008
钢管宽厚比是限制矩形钢管混凝土构件截面设计的主要因素,为增加钢管宽厚比限值,延缓管壁局部屈曲,可在管壁上设置纵向加劲肋.加劲肋的肋数及尺寸显著影响钢管的承载力及管内混凝土的整体性能.论文建立设纵肋矩形钢管混凝土轴压柱的屈曲分析模型,将问题转化为求解均布荷载作用下加载边和非加载板均为固支边界的设纵肋薄板的屈曲荷载,采用能量法推导出构件屈曲荷载及屈曲系数的解析表达式.根据被加劲板的屈曲模式,提出采用最小加劲刚度比进行矩形钢管混凝土轴压构件加劲肋的设计,并给出相应的计算公式,为加劲肋的肋数、截面尺寸及材料性能设计提供指导.
Width-thickness ratio was an important parameter for designing CFRST. Welding longitudinal stiffener on the internal wall of steel pipe could delay the local buckling, which increased the limit of width-thickness ratio. If the stiffener were not enough and its sectional dimension was too small, the local buckling of steel pipe occurred, which induced its bearing capacity seriously. If the stiffener sectional dimension is too large, concrete filled in steel tube would be broken up, which reduced bearing capacity. To solve that problem, this paper studied on local buckling of CFRST with longitudinal stiffener under axial compression and design of longitudinal stiffener. It established buckling analysis model, simplified local buckling analysis as calculating buckling load of thin plate clamped on loading side and unloading side under axial force. It deduced buckling load and buckling coefficient based on the principle of energy. The results showed that buckling mode depended on stiffening rigidity. Therefore, it put forward minimum stiffening rigidity ratio that controlled the stiffener design. This paper also came up with a formula to calculate minimum stiffening rigidity ratio. It provided guidance on designing number, sectional dimension and material performance.
钢管混凝土以承载力高、塑性和韧性好、施工方便、耐火性能和经济效益好等优点广泛用作桁架桥的弦管、拱桥的拱肋、斜拉桥的桥塔及桥墩,成为发展前景广阔的一种结构形式[1].与圆形截面相比,矩形钢管混凝土构件尺寸可以做的更大,连接构造相对简单,施工更为简便,在宽厚比较大的结构中占有绝对优势.钢管宽厚比是限制矩形钢管混凝土截面设计的主要因素[2],宽厚比过大导致钢板在材料屈服破坏前发生面外屈曲; 而宽厚比过小带来构件截面尺寸受限、钢材用量大等问题.为增加钢管宽厚比限值,延缓管壁局部屈曲,可在管壁上设置纵向加劲肋[3].加劲肋尺寸随钢管宽厚比增大而增加,对于截面尺寸较大的矩形钢管混凝土构件,需增大加劲肋高度,影响核心混凝土的整体性能,并给施工带来困难.
矩形钢管混凝土柱受轴压荷载作用发生管壁局部屈曲,可将管内核心混凝土看作刚性材料,假定符合边界条件的变形函数,应用能量法推导钢管屈曲强度公式,确定不同边界条件的屈曲系数和宽厚比限值[3].何保康等[4, 5]将钢板非加载边简化为固支边界,推导矩形钢管混凝土钢管板件的局部屈曲系数为空钢管的2.67倍.莫时旭等[6]进一步将钢板非加载边看作弹性约束,给出了约束刚度与矩形钢管混凝土柱局部屈曲强度的关系式.蔡健等[7, 8]用同样方法推导了带约束拉杆矩形钢管混凝土柱轴压下的局部屈曲系数,分析了约束拉杆参数对钢管宽厚比限值的影响.成戎等[9]进行设纵肋矩形钢管混凝土轴压短柱屈曲系数的变参数分析,讨论了加劲肋尺寸参数对钢管稳定性的影响.在此基础上,本文应用能量法推导设纵肋矩形钢管混凝土柱轴压下的钢管壁局部屈曲强度计算公式,讨论纵肋的肋数、截面尺寸、材料性能对钢管局部屈曲性能的影响,给出外钢管完全加劲的最小加劲刚度比计算公式,提出加劲肋的构造要求和设计计算公式.
对于矩形钢管混凝土轴压柱,管内混凝土可看作刚性材料,钢管壁发生屈曲时由于混凝土的支撑作用只能发生向外凸起变形.且板件长度较宽度大很多,钢板发生屈曲时横向呈一个半波,纵向呈现一系列连续半波,如图1所示.
钢管截面相邻板件受核心混凝土的支承只能发生外凸变形,且在钢管角部始终保持为直角即钢管各板件的纵向边不能发生转动,相当于板件非加载边为固定边.由纵向变形曲线形状及曲线的连续性可知,从一个凸起到另一个凸起的过渡过程中可能出现一阶导数为零的边.两个一阶导数为零的边之间的板件相当于固定边.由此可认为,矩形钢管混凝土轴压柱屈曲分析可简化为求解轴压荷载作用下板的屈曲荷载,其边界条件为加载边和非加载边均为固支边界的薄板,且薄板只能向一侧发生屈曲变形.对于设纵肋矩形钢管混凝土轴压柱,若纵肋加劲刚度足够大,纵肋可提供被加劲板一条支承边,在板件屈曲时加劲肋能够保持挺直,其屈曲模式如图2b所示.若纵肋加劲刚度不够,加劲肋将随被加劲板共同向外凸起变形,只起弹性支承的作用,其屈曲模式与无肋的矩形钢管混凝土相近,如图2a所示.
基于上述分析,设纵肋矩形钢管混凝土轴压柱的屈曲分析可简化为求解均布荷载作用下设纵肋薄板的屈曲荷载,其边界条件为加载边和非加载板均为固支边界的板,且板只能向一侧发生屈曲变形.矩形薄壁钢管发生微小变形的应变能[10]为
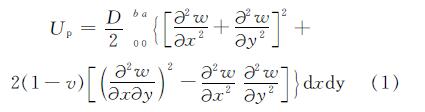
式中:a为板的长度; b为板的宽度; w为挠曲函数; D=(Et3)/(12(1-v2))为单位宽度板的抗弯刚度,其中t为钢板厚度,E为钢板弹性模量,v为钢板泊松比.
钢板受单向均匀轴向压应力σ作用下的外力势能为
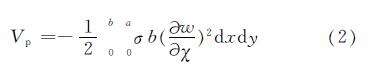
轴压作用下的钢管局部屈曲性能受到纵向加劲肋作用,需要分析加劲肋刚度的影响.单向均匀轴压钢板屈曲时,认为纵向加劲肋随钢板共同挠曲变形,则加劲肋的弯曲应变能Us和所受的外力势能Vs可表示为
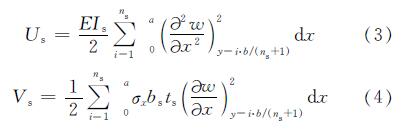
其中bs、ts分别为加劲肋宽度和厚度,Is为加劲肋截面对钢板截面中性轴的惯性矩,Is=1/(12)tsb3s,ns为加劲肋的个数.此时整个体系的总势能为
∏=Up+Vp+Us+Vs(5)
假定矩形板沿长度方向均匀受压,板长为a,板宽为b,板在纵向呈m个半波,在横向呈n个半波的失稳模态,加载边、非加载边均为固支边界情况下,钢板屈曲应满足边界条件:
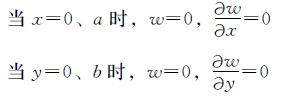
符合该边界条件的屈曲位移函数可设为
wf=f(1-cos(2mπx)/a)(1-cos(2nπy)/b)(6)
将屈曲位移函数(6)式带入式(1)、(2)、(3)、(4)、(5),整理后可得整理后得到总势能Π.
取薄板在纵横向一个半波即m=n=1进行研究.根据势能驻值原理求解临界屈曲应力σ,由(dΠ)/(df)=0,且f≠0得:
当ns=1时
σ=(4(3Db4+3Da4+2Da2b2+EIsb3)t)/(a2b(3bt+8bsts))(7)
当ns>1时
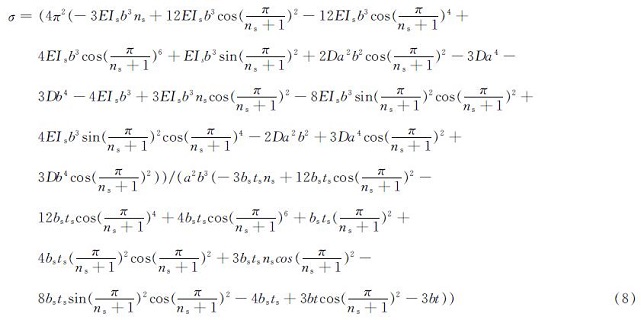
令β=a/b,δ=(bsts)/(bt),γ(EIs)/(Db),其中β为板的长宽比,δ为加劲肋与被加劲板的面积比,γ 为加劲肋的抗弯刚度与被加劲肋板的抗弯刚度之比.由式8可得到屈曲系数k的表达式.
σ=k(π2D)/(b2t)(9)
当ns=1时,k=(4(3+3β4+2β2+8γ))/(β2(3+8δ))(10)
对于无肋的矩形钢管混凝土轴压柱即β=1,δ=0,γ=0,屈曲系数k为10.67,这与文献[4-5]得到的屈曲系数值一致,这验证了本文理论推导过程的正确性.在长宽比β一定时,设纵肋板的屈曲系数随面积比δ的增大而减小,随加劲刚度比γ的增大而增大.
当ns>1时

为充分发挥钢材的强度性能和节约钢材用量,钢板的厚度一般相对较小,但钢板厚度越小即宽厚比越大,其屈曲强度越低.为防止钢板局部发生弹性屈曲通常对矩形钢管混凝土构件外钢管的宽厚比进行限制[11],限定板件发生局部屈曲时的临界应力不能低于钢材的屈曲强度,即σcr≥fy.[12]
基于此,本文拟给出设纵向加劲肋的矩形钢管混凝土轴压构件钢管宽厚比的限值,即板件弹性屈曲临界应力不小于钢材的屈曲强度.
σ=k(π2D)/(b2t)=k/(12(1-υ2))(π2E)/((b/t)2)≥fy(12)
将式12进行整理后,得到:
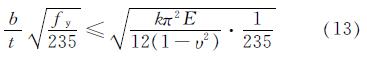
其中,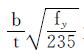 为板件的相对宽厚比.由该式可知,板件相对宽厚比限值主要取决于屈曲系数大小.在此,以设单肋矩形钢管混凝土构件以例, 对于无肋的矩形钢管混凝土轴压柱,δ=0,γ=0,屈曲系数k为10.67.由式18可得,矩形钢管混凝土轴压构件的相对宽厚比理论限值为92.考虑钢板初始几何缺陷及焊接残余应力等因素,对理论宽厚比限值进行折减,《矩形钢管混凝土结构技术规程》[16]推荐轴压构件相对宽厚比限值取为60.对于设单肋矩形钢管混凝土轴压柱,加劲刚度足够大时,相当于在加劲肋处提供固支边界,壁板被分隔为两块子板件,子板件宽度变为b/2,轴压荷载作用下每块子板件各自屈曲,其屈曲应力表示:
为板件的相对宽厚比.由该式可知,板件相对宽厚比限值主要取决于屈曲系数大小.在此,以设单肋矩形钢管混凝土构件以例, 对于无肋的矩形钢管混凝土轴压柱,δ=0,γ=0,屈曲系数k为10.67.由式18可得,矩形钢管混凝土轴压构件的相对宽厚比理论限值为92.考虑钢板初始几何缺陷及焊接残余应力等因素,对理论宽厚比限值进行折减,《矩形钢管混凝土结构技术规程》[16]推荐轴压构件相对宽厚比限值取为60.对于设单肋矩形钢管混凝土轴压柱,加劲刚度足够大时,相当于在加劲肋处提供固支边界,壁板被分隔为两块子板件,子板件宽度变为b/2,轴压荷载作用下每块子板件各自屈曲,其屈曲应力表示:
σ=10.67(π2D)/((b/2)2t)=42.68(π2D)/(b2t)(14)
由式14可知,设纵肋矩形钢管混凝土轴压柱的极限屈曲系数为42.67,相应的子板件宽厚比限值为92,考虑到钢板初始几何缺陷及焊接残余应力等因素影响,本文推荐设纵肋矩形钢管混凝土轴压构件子板件相对宽厚比限值取为60.
加劲肋与被加劲板的抗弯刚度比γ决定着被加劲板的屈曲模式,如图3所示.当加劲刚度不足即γ<γ*时,在荷载作用下,加劲肋随被加劲板一起变形,发生板的整体失稳.其中,γ*为最小加劲刚度比.若完全加劲即γ≥γ*时,加劲肋起到节线的效果,加劲肋之间的子板件发生局部屈曲,子板件的局部屈曲临界应力控制着被加劲板的屈曲应力.此时,进一步加大加劲肋抗弯刚度并不能提高被加劲板的屈曲应力.因而,确定设纵肋矩形钢管混凝土轴压构件最小加劲刚度比是进行加劲肋设计的基础.
首先,本文以设单肋矩形钢管混凝土1轴压构件为例求解最小加劲刚度比.根据式10,令(k)/(β),得到k的最小值函数,此时β0=1/3(81+216γ)1/4,β0为板件的临界长宽比,代入式10,可得:
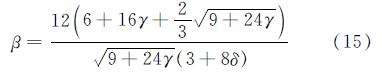
当β≤β0时,最小加劲刚度比的计算需假定肋间子板件在纵横向形成一个半波屈曲变形,即子板件屈曲应力σcrp与被加劲板屈曲应力σ相等,联立两式进而得到:
σ=k(π2D)/(b2t)σcrp(π2D)/((b/2)2t)(16)
k=(4(3+3β4+2β2+8γ))/(β2(3+8δ))=4kp(17)
已知矩形钢管混凝土轴压柱屈曲系数kp为10.67,将其代入式17,可得最小加劲刚度比:
γ*=-0.375+3.75β2+10.67β2δ-0.375β4(18)
当β>β0时,最小加劲刚度比的计算是基于纵横向呈一个半波失稳模型形函数的简化,取β=β0,则
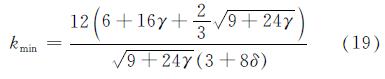
将kp=10.67代入式19,则得最小加劲刚度比:
γ*=9+53.4δ+75.9δ2(20)
综上所述,最小加劲刚度比的计算公式如下:
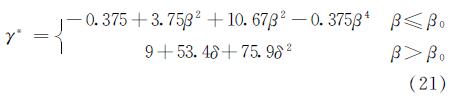
达到最小加劲刚度比后,取被加劲板发生整体失稳时所承受的荷载值等于肋间子板件发生局部屈曲时所承受的荷载.屈曲系数简化如下:
(1)当被加劲板的长宽比不超过临界长宽比,可直接通过形函数进行近似计算.
(2)当被加劲板的长宽比超过临界长宽比,所取用的被加劲板的屈曲系数是采用一系列曲线最低点的屈曲系数.
对于设多肋矩形钢管混凝土轴压柱即ns>1,根据式11,令(ak)/(aβ)=0,得到k的最小值函数,此时β0=(γ+1+γns),代入式11,可得kmin的函数表达式.当β≤β0时,最小加劲刚度比的计算需假定肋间子板件在纵横向形成一个半波屈曲变形,即子板件屈曲应力σcrp与被加劲板屈曲应力σ相等,联立后得到:
σ=k(π2D)/(b2t)σcrp=kp(π2D)/((b/(ns+1))2t)(22)
k=kp(ns+1)2(23)
已知矩形钢管混凝土轴压柱屈曲系数kp为10.67,将其代入式22,可得最小加劲刚度比.
当β>β0时,最小加劲刚度比的计算是基于纵横向呈一个半波失稳模型形函数的简化,取β=β0,则
kmin=(ns+1)2kp(24)
将kp=10.67代入式24,则得最小加劲刚度比γ*.
在此,本文给出常用的设多肋矩形钢管混凝土轴压柱最小加劲刚度比的计算公式,如表1所示.
设计一个设纵肋的薄壁型矩形钢管混凝土柱的外钢管和加劲肋尺寸,外钢管是由四板钢板拼焊而成.外钢管长度a为4 m,宽度b为4 m,板厚t为18 mm,钢材牌号为Q235,弹性模量Ec取为2.06*105 MPa,泊松比νc取为0.3.拟沿长度方向等间距设置三条纵肋,纵肋的板厚ts由6 mm变化到22 mm,肋高bs分别为100 mm、200 mm、300 mm.
外钢管的相对宽厚比为222.2,设置3条加劲肋,则肋间子板件之间相对宽厚比限值为55.5,满足设纵肋矩形钢管混凝土轴压柱的肋间子板件宽厚比限值为60这一规定.
查表1可知,设置3条纵肋相应的长宽比限值和最小加劲刚度比的计算公式.由此,可计算得到在不同肋厚和肋高情况下,纵肋的设计是否属于完全加劲,计算结果如表2所示.
由表2可知,满足完全加劲的纵肋肋高为300 mm,肋厚可分别取为14 mm、18 mm和22 mm.以上算例表明,仅增大纵肋与被加劲板面积比,对加劲刚度比提高不明显; 增大纵肋的高度是一种有效提高加劲刚度比的措施.
(1)设纵肋矩形钢管混凝土轴压柱的屈曲分析可简化为求解均布荷载作用下设纵肋薄板的屈曲荷载,其边界条件为加载边和非加载板均为固支边界的板,且板只能向一侧发生屈曲变形.基于能量原理,论文给出了一种求解设纵肋矩形钢管混凝土轴压柱屈曲系数的解析算法,并验证了算法的可靠性.
(2)最小加劲刚度比是进行矩形钢管混凝土加劲肋设计的基础.当加劲刚度不足即达不到最小加劲刚度比时,轴向荷载作用下加劲肋随被加劲板一起变形,发生板的整体失稳.若完全加劲即达到最小加劲刚度比时,加劲肋起到节线的效果,肋间子板件的局部屈曲临界应力起控制作用,继续增大加劲肋抗弯刚度并不能提高被加劲板的屈曲应力.
(3)给出了设单肋、多肋矩形钢管混凝土轴压构件外钢管最小加劲刚度比的计算公式,提出了钢管肋间子板件相对宽厚比限值,为加劲肋的设计如肋数、截面尺寸、材料等提供依据.