基金项目:国家自然科学基金项目(51178387)
第一作者:何芳社(1962-),男,教授,硕士生导师,主要研究结构与复杂介质的相互作用.E-mail: xymmyf0927@sina.com
(School of Science, Xi'an Univ. of Arch. & Tech., Xi'an 710055, China)
transversely isotropic; two-parameter foundation; the principle of minimal potential energy; rectangular thin plate; Ritz method
DOI: 10.15986j.1006-7930.2018.05.021
弹性地基板是建筑工程中常见的构件,对其进行分析具有重要意义.对于工程中的大量由沉积作用形成的天然地基和分层碾压填筑而成的人工地基,采用横观各向同性地基模型更接近工程实际地基.本文将地基—板作为一个整体系统,利用最小势能原理,经过变分运算,推导建立了横观各向同性双参数弹性地基上矩形薄板弯曲的控制方程及其相应的边界条件.然后选取合理的挠度试函数,采用里兹法,对受横向荷载作用的四边自由矩形薄板进行了数值分析.计算表明:通过与其他文献的结果对比,两者吻合良好.所用理论在研究地基板的相互作用中具有普适性,为横观各向同性双参数弹性地基的应用奠定了基础.
The plate on elastic foundation is the common structural component, so it is very important to have a detailed analysis about this plate for researchers. The transversely isotropic body will be more reasonable due to the experimental evidence for the large number of natural foundations formed by sedimentation and artificial foundations formed by stratifying and rolling in the project. The article completed the basic theory of plates by the principle of minimal potential energy and the variational calculus with the foundation and the plate as a whole system. The governing equations and the boundary conditions of plates on the bi-parameter foundations are given. The displacement function for meeting the correct boundary condition is selected. Ritz method is used to analyze the bending of plate, giving the deflection for the bending of rectangular plate with four free edges under lateral loads. In the end, the numerical calculations are accomplished. And compared to other literature, their results are coincident. The theory has some universality for analyzing the interaction between plate and elastic foundation. The method lays the foundation for the application of the transversely isotropic two-parameter elastic foundation.
研究结构物基础与支撑土介质间的相互作用对结构工程和岩土工程均具有重要意义.随着建设项目的不断增多,出现了许多梁状、板状和壳型的结构物,相应地对于基础与地基提出更高的标准和要求.特别是基础工程具有隐蔽性,对于结构的安全和经济方面会有重大的影响; 工程中质量事故有一部分出现在基础与地基中,不但损失巨大,而且难以采取合适的措施来加固.学术界和工程界致力于如何将这些工程实例合理地简化为相应的弹性地基上的梁、板、壳的问题,并进行更加准确且简便的计算.针对弹性地基上梁、板、壳的模型,国内外专家学者都进行了许多富有成果的工作.比如 Vallabhan C V G等对双参数地基上板、梁的能量和参数及内力、边界条件进行了求解说明[1].Yang用有限元法分析双参数地基时指出还没有方法可以计算参数值[2].Jones和Xenophontos推导出了双参数地基中参数和表面变形的联系[3].Nogami和Lam分析了地基板的双参数模型,然而此方法仅限于平面应变[4].Celep Z分析研究了无拉力情形下弹性地基上矩形板的弯曲[5].国内方面,王克林、黄义[6]和张福范、黄晓梅[7]用叠加法分析探讨了地基上矩形板体的弯曲; 陈叔陶等根据变分原理通过Ritz法分析求解了弹性地基上板体的弯曲[8]; 阎红梅、崔维成等引入新挠度函数,通过伽辽金法对弹性地基上矩形板进行了研究[9].
前人对地基板经典问题的研究存在有待深入探讨的方面.比如现有的弹性地基理论体系认为介质是连续、线弹性、均匀和各向同性的,且服从小变形假设.对应的弹性地基模型可总结为:文克尔模型、双参数模型和弹性半空间模型[10].但试验表明许多地基的性质更接近于横观各向同性.鉴于目前对横观各向同性地基上矩形板的研究并不充分,本文考虑地基横观各向同性,研究双参数地基上矩形板的弯曲问题,对地基与矩形薄板的相互作用进行系统的分析.首先利用最小势能原理,经过变分运算,建立了横观各向同性弹性地基上板的控制微分方程和边界条件,该结果可退化到经典的双参数弹性地基板理论.综上所述,本文的创新之处在于:从能量角度出发,考虑实际土体的横观各向同性的属性,改进和丰富了符拉索夫双参数弹性地基模型,具有一定的学术与应用价值.为验证理论正确性,最后利用里兹法进行了数值计算,效果较好.
将地基—板作为一个整体,该系统的总势能泛函[11-12]为
U=UP+US+Uq(1)
式中,各物理量依次为总势能,板的形变势能,地基的形变势能和外力势能.
根据弹性薄板理论[13],得板的形变势能
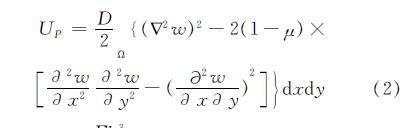
其中:D=(Eh3)/(12(1-μ2))是板的弯曲刚度; E和μ是板的弹性模量和泊松比; w是板的挠度; Ω是矩形薄板区域,即x∈[0,a],y∈[0,b].
根据弹性理论中弹性体的形变势能,有
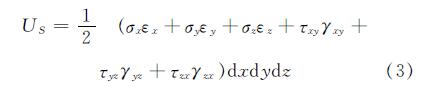
假定地基的水平位移分量us=0,vs=0,竖直位移分量ws(x,y,z)=w(x,y)φ(z),φ(z)为衰减函数,且满足条件φ(0)=1,φ(H)=0.令E1,μ1为各向同性面内变形模量和泊松比,E2,μ2为各向同性面法线方向变形模量和泊松比,G为与各向同性面垂直的平面内剪切模量.则横观各向同性弹性地基的本构关系和几何关系[14][15]为
{σx=C11εx+C12εy+C13εz,τxy=C66γxy
σy=C12εx+C11εy+C13εz,τyz=C44γyz
σz=C13εx+C13εy+C33εz,τzx=C44γzx(4)
其中的Cij是地基土的物性常数,与工程常用的材料弹性常数有如下关系
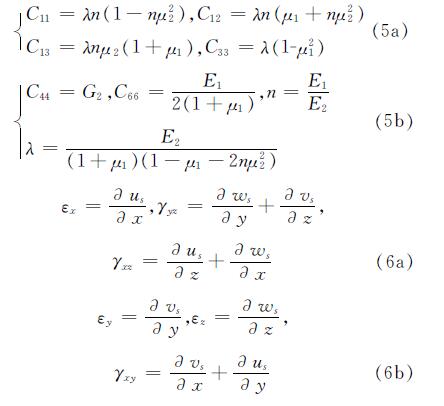
将上面(4)和(6)式代入(3)式,得地基的形变势能
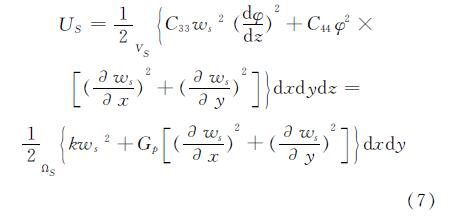
其中:VS为地基体积区域; ΩS为地基表面区域.
k=C33∫H0((dφ)/(dz))2dz,Gp=C44∫H0φ2dz(8)
外力势能为
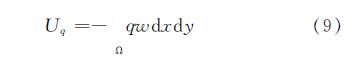
由最小势能原理,经过变分,可得板控制方程

及板外地基控制方程

α2=k/Gp(12)
经过计算,并注意到变分项的任意性,可得关于x=a边和(a,b)角点的边界条件如下
若边界为固定边,则挠度与转角为零,即

若边界为简支边,则挠度与弯矩为零,即

若边界情况为自由边,得
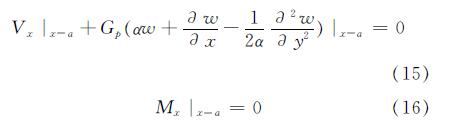
当(a,b)为自由角点时,则δw为零,得
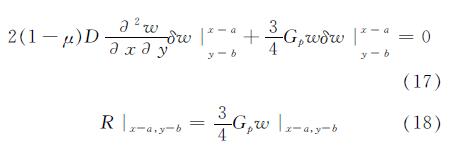
矩形薄板其它边界和角点的条件与上类似.令物性常数E1=E2=Es,μ1=μ2=μs,C44=Gs,可将横观各向同性地基退化为各向同性地基,得到C33=(Es(1-μs))/((1+μs)(1-2μs)).那么式(10)—式(18)退化后与传统的各向同性双参数地基上矩形板的控制方程和边界条件保持一致[16-17],即方程表达形式没有变化,但其中地基土的双参数发生变化.表明土体的各向同性属性是横观各向同性属性的一种特殊情况,而横观各向同性则更具有普遍的意义.
采用里兹法对弹性地基上矩形薄板进行计算.对于四边自由的边界条件而言,可以选取如下的挠曲试函数
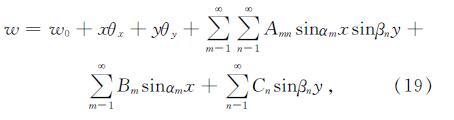
其中:αm=(mπ)/a,βn=(nπ)/b,(m,n=1,2,3…); 而w0,θx,θy,Amn,Bm,Cn是待定系数.具体分析如下:w0+xθx+yθy为整个板的刚体位移,中间的∑∞m=1∑∞n=1Amnsinαmxsinβny为板任意位置上的二维挠度,最后两项表示板在对应方向上的挠曲.
由下列各式
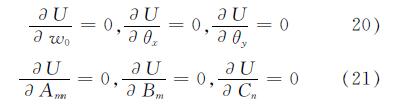
分别整理后可以得到如下系列方程组,即
[kab+2Gpα(a+b)+3Gp]w0+
((ka2b)/2+Gpαab+Gpαa2+(3Gpa)/2)θx+
((kab2)/2+Gpαab+Gpαb2+(3Gpb)/2)θy+
∑∞m=1∑∞n=1k/(αmβn)[1-(-1)m][1-(-1)n]Amn+
∑∞m=1((kb)/(αm)+(2Gpα)/(αm)+(Gpαm)/(2α))[1-(-1)m]Bm+
∑∞n=1((ka)/(βn)+(2Gpα)/(βn)+(Gpβn)/(2α))[1-(-1)n]Cn=
∫a0∫b0[q(x,y)]dxdy(22)
((ka2b)/2+Gpαab+Gpαa2+(3Gpa)/2)w0+
[(ka3b)/3+Gp(ab+αa2b+(2αa3)/3+(3a2)/2)]θx+
[(ka2b2)/4+Gp((αab2)/2+(αa2b)/2+(3ab)/4)]θy+
∑∞m=1∑∞n=1(-ka)/(αmβn)(-1)m[1-(-1)n]Amn+
∑∞m=1[(-kab)/(αm)-(2Gpαa)/(αm)-(Gpαma)/(2α)](-1)mBm+
∑∞n=1[(ka2)/(2βn)+(Gpαa)/(βn)+(Gpβna)/(4α)][1-(-1)n]Cn=
∫a0∫b0[q(x,y)x]dxdy(23)
((kab2)/2+Gpαab+Gpαb2+(3Gpb)/2)w0+
[(ka2b2)/4+Gp((αa2b)/2+(αab2)/2+(3ab)/4)]θx+
[(kab3)/3+Gp(ab+αab2+(2αb3)/3+(3b2)/2)]θy+
∑∞m=1∑∞n=1(-kb)/(αmβn)(-1)n[1-(-1)m]Amn+
∑∞m=1[(kb2)/(2αm)+(Gpαb)/(αm)+(Gpαmb)/(4α)][1-(-1)m]Bm+
∑∞n=1[(-kab)/(βn)-(2Gpαb)/(βn)-(Gpβnb)/(2α)](-1)nCn=
∫a0∫b0[q(x,y)y]dxdy(24)
{k/(αmβn)[1-(-1)m][1-(-1)n]}w0+
(-ka)/(αmβn)(-1)m[1-(-1)n]θx+
(-kb)/(αmβn)(-1)n[1-(-1)m]θy+
1/4[Dab(α2m+β2n)2+kab+Gpab(α2m+β2n)]Amn+
[(Da)/2((α4m)/(βn)+μα2mβn)+(ka)/(2βn)+(Gpα2ma)/(2βn)]x;…
…[1-(-1)n]Bm+
[(Db)/2((β4n)/(αm)+μαmβ2n)+(kb)/(2αm)+(Gpβ2nb)/(2αm)]x;
[1-(-1)m]Cn=
∫a0∫b0[q(x,y)sinαmxsinβny]dxdy
(m,n=1,2,3,···)(25)
((kb)/(αm)+(2Gpα)/(αm)+(Gpαm)/(2α))[1-(-1)m]w0+
[(-kab)/(αm)-(2Gpαa)/(αm)-(Gpαma)/(2α)](-1)mθx+
[(kb2)/(2αm)+(Gpαb)/(αm)+(Gpbαm)/(4α)][1-(-1)m]θy+
∑∞n=1[(Dα2ma)/(2βn)(α2m+μβ2n)+(ka)/(2βn)+(Gpα2ma)/(2βn)]x;
[1-(-1)n]Amn+1/2[Dα4mab+kab+
Gp(2αa+α2mab+α2ma)]Bm+
∑∞n=1[Dμαmβn+k/(αmβn)][1-(-1)m]x;
[1-(-1)n]Cn=∫a0∫b0[q(x,y)sinαmx]dxdy
(m,n=1,2,3,…)(26)
((ka)/(βn)+(2Gpα)/(βn)+(Gpβn)/(2α))[1-(-1)n]w0+
[(ka2)/(2βn)+(Gpαa)/(βn)+(Gpaβn)/(4α)][1-(-1)n]θx+
[(-kab)/(βn)-(2Gpαb)/(βn)-(Gpβnb)/(2α)](-1)nθy+
∑∞m=1[(Dβ2nb)/(2αm)(β2n+μα2m)+(kb)/(2αm)+(Gpβ2nb)/(2αm)]x;
[1-(-1)m]Amn+1/2[Dβ4nab+kab+
Gp(2αb+β2nab+β2nb)]Cn+
∑∞m=1[Dμαmβn+k/(αmβn)][1-(-1)m]x;
[1-(-1)n]Bm=∫a0∫b0[q(x,y)sinβny]dxdy
(m,n=1,2,3,…)(27)
可见未知数的数目和方程的个数相等,问题可解.以下算例中均取m=50,n=50.
例1 取板的弹性模量E=1.96×104 MPa,泊松比为μ=0.167,地基的弹性模量为Es=39.2 MPa,泊松比为μs=0.4,深度为H=0.6 m,地基参数γ=1.55,板宽a=1 m,板厚h=0.04 m,集中力P=98 kN,均布荷载q=9.8 kN/m2.
图2是依据本法绘制的双参数地基上矩形薄板的挠度图,图3是弯矩图,宏观定性看出图形的趋势走向及数值大小与实际符合.表2中第一行是双参数地基矩形薄板的精确解[18-19],第二行是本文由横观各向同性弹性地基退化为各向同性弹性地基的计算结果.微观定量进行比较,两者结果吻合良好,百分误差都在可接受的较小范围之内,证明了分析结果的可靠性.
例2 矩形薄板的物理和几何参数,荷载情况同例1,横观各向同性地基参数选取如下,Es1=39.2 MPa, Es2=29.4 MPa,μ1=0.4,μ2=0.4,G=14 MPa,计算结果见文后的表3.
由于现有文献中没有关于横观各向同性双参数地基上矩形薄板受横向荷载作用的弯曲挠度,所以本算例只与退化后的各向同性双参数地基上矩形薄板的结果相比较.
首先,经过编程运算,横观各向同性双参数地基上受横向荷载作用的矩形薄板的变形图与图2相似,也就是图形的趋势走向及数值大小与实际吻合.其次,定量地分析,表3中第一行是本文各向同性双参数地基板的挠度,第二行是本文横观各向同性双参数地基板的计算结果.经过比较,同性地基情况解略大于横观各向同性地基情况的解.定性分析原因在于地基土体假设为横观各向同性体,相比于各向同性体而言,土体的本构关系有所不同; 也就是在对横观各向同性地基假定弹性常数时,弹性模量比各向同性地基土的较小,从而导致横观各同性双参数的地基参数k变大,所以板与地基的变形局部变小.最后,值得一提的是,关于结果符合工程实际的讨论中,本文只在理论上给出证明,即采用更接近工程实际情况的横观各向同性地基来推导计算,核心在于其本构关系不同于经典的各向同性双参数地基; 缺少通过原位试验来测量矩形薄板受载后的变形结果,或者利用有限元软件来模拟计算,这将是之后科研的方向和目标.
另外,
参考文献[18-19]中采用了一些旧的单位制,为了既可方便地与已有结果进行对比,同时又遵循国标单位制,现给出基本的单位换算关系1 t=103 kg,1 Pa=1 N/m2,g=9.8 m/s2
分析了横观各向同性双参数弹性地基上矩形薄板的弯曲问题,主要工作为:考虑地基土体的横观各向同性,推导出地基—板系统的形变势能,利用最小势能原理,通过变分运算,建立了弹性地基上矩形薄板弯曲的控制方程和边界条件; 然后选取挠度试函数,采用里兹法求解四边自由矩形板受横向荷载的弯曲挠度.得到如下几点结论:
(1)从能量方面出发,利用最小势能原理推导出横观各向同性双参数地基上矩形薄板弯曲的控制方程和边界及角点条件.考虑实际地基土体的横观各向同性,改进和丰富了符拉索夫双参数弹性地基模型,可促进其更加广泛地应用.
(2)横观各向同性双参数弹性地基模型,与Vlasov双参数弹性地基模型一样,用两个独立参数表示抗压和抗剪性能.主要区别在于考虑地基土体横观各向同性时,由土体本构关系不同而导致的双参数具体计算表达形式不同.
(3)选取合适的挠度函数,将地基上板受横向荷载作用的控制微分方程问题转化为代数方程组的求解问题.算例分为退化成各向同性双参数和横观各向同性双参数地基两种.模型退化过程中,通过与其他文献的计算结果对比,两者吻合良好,证明了本文理论推导和计算结果的正确性.
(4)结果表明,考虑地基土体的横观各向同性属性时,矩形板和地基的变形会与各向同性弹性地基的情况不同,即地基模型的假设简化会对板的弯曲产生一定的影响,所受影响的大小由选取的横观各向同性地基土体的物性常数来决定.
总之,本文对于横观各向同性双参数地基上四边自由矩形薄板的弯曲问题进行了相关研究.修正的模型和方法具有一定的创新性,相关成果和结论具有重要的理论意义,同时对于实际工程问题的解决和设计仿真软件的开发等方面均具有指导价值和参考作用.