各国对于受弯承载力的计算基于以下假设:(1)截面应变保持平面;(2)不考虑混凝土的抗拉强度;(3)FRP筋被拉断前应力-应变关系为线弹性;(4)FRP筋与混凝土之间粘结性能良好.混凝土的应力-应变关系参照本国的混凝土规范.

根据以上假定,各国规范对FRP筋混凝土梁正截面受力的简化方法基本相同,参照本国混凝土规范对混凝土应力-应变关系的规定,将压区混凝土应力曲线图等效成为矩形应力图,见图1.

图1 FRP筋混凝土梁正截面应力-应变分布
Fig.1 Stress and strain distribution of FRP-RC beams

按照配筋率对FRP筋受弯构件的破坏模式进行分类,定义纵向受拉FRP筋达到设计强度与受压区混凝土破坏同时发生的配筋率为平衡配筋率ρ_fb,计算公式见表1.认为当ρ_f>ρ_fb,试件发生混凝土压碎破坏,简称受压破坏,而ρ_f<ρ_fb时,试件发生FRP筋拉断破坏,简称受拉破坏.然而,大量试验研究表明,当ρ_f高于ρ_fb一定范围内,构件仍有可能发生受拉破坏,因此GB 50608将ρ_f=1.5ρ_fb作为FRP筋有效设计应力计算公式的分段点,而ACI 440.1R规定ρ_f>1.4ρ_fb时采用受压破坏承载力公式进行设计.

ACI 440.1R、ISIS和CNR-DT 203给出的FRP筋混凝土梁受拉、受压破坏正截面承载力计算公式基本相同,均根据受力平衡及应变协调条件进行理论推导得到.其中ACI 440.1R受拉破坏计算公式采用界限受压区高度代替计算受压区高度,使计算简化且结果偏安全.GB 50608结合理论模型及对试验数据的统计分析,当ρ_f≤ρ_fb时,将FRP筋受弯构件内力臂系数γ_f修正为0.9; 当ρ_f>ρ_fb时,以ρ_f=1.5ρ_fb为分界点分段拟合试验设计参数,建立了FRP筋有效设计应力值f_fe的经验表达式.

本文统计了328组FRP筋混凝土梁正截面受弯承载力试验数据,考虑构件截面宽度b,有效高度h_0f,混凝土强度f_c'、FRP筋抗拉强度f_fu、弹性模量E_f及纵筋配筋率ρ_f、配筋率与平衡配筋率之比ρ_f/ρ_fb等影响因素,对其进行统一整理,见表2.

根据我国《混凝土结构设计规范》和欧洲模式规范^[47]对混凝土强度进行统一换算,各规范设计公式中的材料分项系数均不予考虑.综合各国规范对FRP筋梁受弯破坏模式的分类方法,将规范计算值分为ρ_f<ρ_fb、ρ_fb≤ρ_f、ρ_fb≤ρ_f<1.5ρ_fb和1.5ρ_fb≤ρ_f四组并分别与试验值进行对比,结果见表3.图2为试验值与各国规范计算值比值的分布情况,μ和σ分别表示均值和标准差,μ±σ表示偏差范围.

表1 FRP筋混凝土梁正截面受弯承载力计算模型
Tab.1 Normol section flaexural bearing capacity calculation model of FRP reinforced comcret beams

表2 FRP筋混凝土受弯构件试验数据概况
Tab.2 Database of concrete flexural members reinforced with FRP

表3 规范计算值与试验值对比
Tab.3 Comparisons between calculated and experimental values

图2 规范模型计算对比分析
Fig.2 Comparisons to code provisions

结果表明,在ρ_f<ρ_fb和ρ_fb≤ρ_f<1.5ρ_fb两种情况下,规范计算值与试验值均吻合良好,离散程度均较小; 当1.5ρ_fb≤ρ_f时,试验值均超过规范计算值20%以上,这是由于受压破坏由混凝土极限压应变控制,而其实际值一般大于规范规定值.ACI 440.1R混凝土极限压应变取值为0.003,GB 50608为0.003 3,ISIS和CNR-DT 203为0.003 5,对于FRP筋梁受弯承载力,ACI 440.1R的计算方法最为保守,GB 50608和ISIS规范次之,CNR-DT 203计算值最接近试验值.可以看出,混凝土极限压应变的取值是影响受压破坏试件承载力计算值准确程度的重要因素.

采用高估承载力试件数量百分比作为计算公式可靠程度的评价指标,通过表3可以发现:当ρ≤1.5ρ_fb时,承载力被高估的试件数量均超过40%,表明受拉破坏试件的计算方法一定程度上高估了FRP筋的极限应力,使计算结果偏于不安全; 当1.5ρ_fb≤ρ_f时,ACI 440.1R计算方法最可靠,CNR-DT 203安全可靠度相对最低,GB 50608和ISIS居于两者之间.

受压破坏FRP筋混凝土梁的正截面承载力计算模型应力-应变分布如图1所示,根据受力平衡及应变协调条件可得:

A_ff_f=α₁f_cxb(1)

f_f=E_fε_cu(β₁h_0f-x)/x(2)

式中,x为混凝土界限受压区高度.

联合式(1)、式(2)可得:

为简化式(3),将发生受压破坏且ρ_f>1.5ρ_fb试件的承载力试验值M_exp带入式(4),得到等效矩形受压区混凝土高度试验值x_exp:

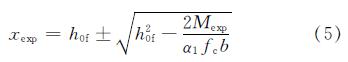
利用SPSS软件将参数ρ_f/ρ_fb和c_b/x_exp进行拟合,见图3.其中c_b为界限受压区高度,计算公 式为:

c_b=((ε_cu)/(ε_cu+f_fd/E_f))h_0f(6)

则式(3)可简化为

x=((ρ_f)/(ρ_fb))^0.422*(c_b)/(1.191)(7)

结合式(4)、式(7),当ρ_f≥1.5ρ_fb时,FRP筋混凝土梁正截面受弯承载力可按式(8)进行计算.

M_n=α₁f_cb((ρ_f)/(ρ_fb))^0.422*

(c_b)/(1.191)[h_0f-((ρ_f)/(ρ_fb))^0.422*(c_b)/(2.382)](8)

图3 ρf>1.5ρfb时cb/x与ρf/ρfb关系
Fig.3 Relationship between w/c and kc when ρf>1.5ρfb

采用各国规范及本文建议公式对受压破坏FRP筋混凝土梁承载力进行计算,结果见表4.从表中可以看出,与各国规范的计算模型相比,本文建议公式的计算值与试验值的吻合程度最高,离散程度与各国规范相近,但高估承载力试件数量百分比为51.2%,表明本文建议公式偏于不保守.

表4 模型计算值与试验值对比
Tab.4 Theoretical values compared with the test results

为了使计算值具有一定的安全储备,对本文建议公式提出一强度修正系数φ,使M_exp/φM_pred>1的保证率不小于95%,φ的取值可按下式计算:

φ=μr+1.645σr(9)

式中μ_r,σ_r分别为M_exp/M_pred的均值和方差.通过对受压破坏FRP筋梁进行统计分析,得φ=1.45.