(1)假设地基作用面不光滑,摩擦力很大.整个地基产生贯穿至基底的剪切破坏,产生持续的滑动,基底下局部土体与基础同时移动,从而该土体一直保持弹性状况,区域Ⅰ为弹性楔体.该 局部土体与滑动土体分界线用ab表示,并假设分界线ab与基础底平面的夹角用ψ表示,如图1所示.

图1 基底粗糙情况下的滑动面形状
Fig.1 Sliding surface shape of rough base

(2)径向剪切区域Ⅱ与朗金被动区域Ⅲ形成滑动区域,且所有滑动区的土体(区域Ⅰ除外)均保持在塑性平衡状况,区域Ⅱ的界线bc用以下公式表达:

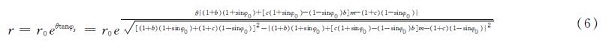
式中: r₀为初始位置矢量,θ为任意位置矢量r与初始位置矢量r₀的夹角.

区域Ⅲ的界线cd是一条直线,与水平面的夹角为45°-φ_s/2.

(3)考虑在基础两侧地基上施加均布超载q=γD,来抵消土体抗剪强度的影响.

由2.1中的假设条件,通过图2所示的区域Ⅰ三角形aba₁的平衡关系,推导出整个剪切破坏情况下的极限荷载表达式:

图2 区域Ⅰ弹性楔体受力示意图
Fig.2 Stress diagram of elastic wedge in Region I

Q_u=2P_pcos(ψ-φ_s)-1/4γB²tanψ+

(4c₀cosφ₀{(1+b)(1+sinφ₀)+[c(1+sinφ₀)-(1-sinφ₀)b]m-(1+c)(1-sinφ₀)}B)/([(1+b)(1+sinφ₀)+(1+c)(1-sinφ₀)]²-{(1+b)(1+sinφ₀)+[c(1+sinφ₀)-(1-sinφ₀)b]m-(1+c)(1-sinφ₀)}²)(7)

式中:γ为基础以下土体的重度,B为基础底部宽度,c₀和φ₀为基础以下土体的抗剪强度参数; 作用力P_p为一合力,由基础以下土体的粘聚力c₀、基础以下土体的重度γ产生的被动土压力和超载q组成,其作用面为区域Ⅰ的分界面ab,即

P_P=P_Pc+P_Pq+P_Pγ(8)

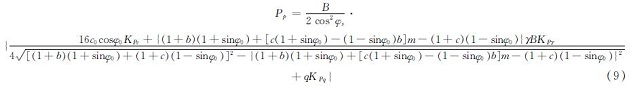
式中:K_Pc=(cosφ_s)/(cosψ)cotφ_s[e^{((3π)/2+φ_s-2ψ)tanφ_s}(1+sinφ_s)-1];

K_Pq=(cos²φ_s)/(cosψ)e^{((3π)/2+φ_s-2ψ)tanφ_s}tan(π/4+(φ_s)/2);

K_pγ为基础以下土体的重度γ所产生的被动土压力的作用系数,确定K_pγ需要采用试算方法.

联立公式(7)与公式(9)推导得出:

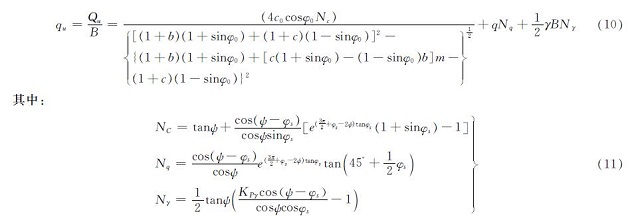
式中,N_c、N_q、N_γ为无法量化的承载力系数指标,只和φ₀有关.

式(10)是以基底粗糙为条件推导出的,并且图2中ψ是未知的.故作如下假定:

(1)假定基础完全粗糙.此时作出如下假定:认为ψ=φ_s,基础底部滑动面形状如图3.

图3 基底完全粗糙情况下的滑动面形状
Fig.3 Sliding surface shape of completely rough base

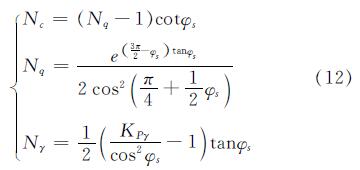
从式(12)可知:系数N_c、N_q、N_γ均受到基础以下土颗粒间摩擦角φ₀的影响,一般需要通过试算确定被动土压力系数K_pγ.

工程运用上为了方便,对于系数N_γ,往往联合太沙基经验公式,采用如下式确定:

N_γ=1.8(N_q-1)tanφ_s(13)

(2)假定基底完全光滑.则区域Ⅰ的土体状态转变成朗金主动状态,从而使得区域Ⅰ与区域Ⅱ和区域Ⅲ共同构成一个完整的滑动区,这时区域Ⅰ的界线ab与水平面的夹角ψ(如图3～图4所示)有如下表达式:

ψ=45^°+1/2φ_s(14)

将ψ代入式(11)中,可分别得到此条件下的系数N_c、N_q、N_γ.

图4 基底完全光滑情况下的滑动面形状
Fig.4 Sliding surface shape of completely smooth base

3.1.1 当基础底部为完全粗糙状态时,根据题设条件φ₀=22°计算得出承载力系数N_c=20,N_q =10,N_γ=7.最后解得地基极限承载力q_u=1 258.0 kPa.

3.1.2 当基础底部为完全光滑状态时,根据题设条件φ₀=22°计算得出承载力系数N_c=16.88,N_q =7.82,N_γ=4.96.最后解得地基极限承载力q_u=988.5 kPa.

地基承载力达到其极限值,此时地基处于屈服破坏的临界状态,中间主应力参数m=1.

当基础底部为完全粗糙状态时,根据题设已知条件,计算得到承载力系数N_c=27.5,N_q =14.78,N_γ=12.3.从而最终解得极限承载力为q_u=2 017.7 kPa.

当基础底部处于完全光滑状态时,根据题设已知条件,解得承载力系数N_c=22.8,N_q =12.3,N_γ=10.最后解得极限承载力为:q_u=1 668.9 kPa.

地基承载力达到其极限值,此时地基处于屈服破坏的临界状态,此时中间主应力参数m=1.

当基础底部处于完全粗糙时,假设系数b(0≤b≤1)分别取0、0.2、0.4、0.6、0.8、1,解得极限承载力如下表1所示.

表1 完全粗糙基底条件下的地基极限承载力值
Tab.1 Ultimate bearing capacity of foundation with completely rough base

当基础底部处于完全光滑状态时,假设系数b(0≤b≤1)分别取0、0.2、0.4、0.6、0.8、1,解得极限承载力如下表2所示.

表2 完全光滑基底条件下的地基极限承载力值
Tab.2 Ultimate bearing capacity of foundation with completely smooth bases

地基承载力达到其极限值,此时地基处于屈服破坏的临界状态,此时中间主应力参数m=1.利用上文中推导的公式分别计算.

(1)当基础底部处于完全粗糙状态时,系数b与c分别在0～1之间取值,从而解得相应的极限承载力值,如表3所示,并绘制了此条件下系数b、c与q_u之间的关系图,如图5所示.

表3 完全粗糙基底条件下的地基承载力值
Tab.3 Ultimate bearing capacity of foundation with completely rough base

图5 完全粗糙基底条件下系数b、c与qu之间的关系图
Fig.5 Correlation graphs between b, C and qu on completely rough base

(2)当基础底部处于完全光滑状态时,系数b与c分别在0～1之间取值,最终解得相应的极限承载力值,如表4所示,并绘制了此条件下系数b、c与q_u之间的关系图,如图6所示.

表4 完全光滑基底条件下的地基承载力值
Tab.4 Ultimate bearing capacity of foundation with completely smooth base

图6 完全光滑基底条件下系数b、c与qu之间的关系图
Fig.6 Correlation graphs between b, c andqu on completely smooth base