对于古木结构而言,在工业振动引起的波动应力作用下,各部分的振动具有相同的频率,且整个结构的振动形成一个完整的空间振动,其振型曲线接近剪切型振动曲线.文献[9]在单层殿堂、亭子计算时采用等截面剪切悬臂杆模型; 两层楼阁计算时采用阶形截面剪切悬臂杆模型; 两层以上的楼阁包括木塔计算时采用变截面剪切悬臂杆模型.本文将古建筑木结构简化为剪切悬臂杆模型进行计算.

多层古建筑木结构建筑,木结构梁柱采用半刚性连接,屋顶采用厚重的屋盖,围护结构采用填充墙,结构形式为木框架结构.本文采用变截面剪切悬臂杆对古建筑木结构进行模拟分析,如图1所示.古建筑木结构在水平荷载作用下的变形主要由两部分组成:一是由于古建筑木结构层间剪力使梁、柱发生的弯曲变形; 二是由于古建筑木结构层间构件的相互错动及楼板平动而产生的整体剪切变形.在交通激励荷载作用下,古建筑木结构楼层的水平剪力会随着木结构层数的增加而逐渐增大,即底部楼层柱底的水平剪力最大,顶层柱顶的水平剪力最小,如图1所示.为了方便建立木结构势能泛函数,本文对交通随机激励荷载产生的层间剪力进行简化,可根据底部弯矩相等或结构底部剪力相等的原则将对荷载对木结构的作用力简化成三角形分布形式,如图1所示.在三角形荷载作用下,木结构变截面剪切悬臂杆任意一点的应力分量σ_y=σ_z=τ_yz=τ_zx=0,σ_x≠0,τ_xy≠0^[10].对于平衡状态的弹性体,剪切悬臂杆在该点处的应变能U:

U=1/2(σ_xε_x+τ_xyγ_xy)dV

=((σ²_x)/(2E)dA_i)dx+((τ²_xy)/(2G)dA_i)dx(1)

式中:A_i为古建筑木结构各层等效截面面积; 等式右侧第一项表示弯曲变形产生的应变能,第二项表示剪切变形产生应变能.

由于古建筑木结构在水平荷载作用下的变形主要是以剪切变形为主,剪切变形产生应变能较大,而弯曲变形产生的应变能比较小,因此本文只考虑木结构的剪切变形^[10].

U=1/2τ_xyγ_xydV=((τ²_xy)/(2G)dA_i)dx(2)

对于古建筑木结构的势能由两部分组成:结构剪切变形产生的势能和外荷载产生的势能.在图1所示模型中,设任意一点结构所受到的作用力为q(x),结构受力后的位形如图虚线所示,则结构的势能为所有力在结构由初始状态变化到虚线所示状态做的功之和.

图1 木结构剪切悬臂杆侧移
Fig.1 Lateral of shear cantilever pole

u'=(du(x))/(dx)=γ=τ/G=(Qμ_s)/(GA_i)(3)

式中:u(x)为木结构侧移曲线; μ_s为木结构剪切因子,可通过能量积分法得到.

则沿木结构剪切悬臂杆竖直高度上,任意一点处的剪应力,为

τ=(QS^*)/(Ib)(4)

将(3)、(4)式代入(2)式,得

U=_H(GA_i)/(2μ²_s)[u'(x)]²dx(5)

当木结构剪切悬臂杆模型从实际位形返回初始位形时,荷载方向和运动方向相反,需克服外力做功,则外荷载所具有势能,为

V=-W=-_Hq(x)u(x)dx(6)

由(6)、(7)式可得木结构总势能的泛函数.

Π=U+V=_H(GA_i)/(2μ²_s)[u'(x)]²dx-_Hq(x)u(x)dx

=_H{(GA_i)/(2μ²_s)[u'(x)]²-q(x)u(x)}dx(7)

设图1所示木结构剪切悬臂杆模型总高度为H,则沿该模型整体总势能泛函数为

Π(u)=^H₀{(GA_i)/(2μ²_s)[u'(x)]²-q(x)u(x)}dx(8)

其中,u(x)∈[0,H],根据最小势能原理可知,使泛函Π(u)取最小值的曲线为木结构剪切悬臂杆模型真实u(x)侧移曲线^[5],将式(8)积分号内的表达式记为F(x, u, u').

F(x, u, u')={(GA_i)/(2μ²_s)[u'(x)]²-q(x)u(x)}(9)

由泛函数极值的必要条件和泛函数的变分公式,对任意一点δu都有

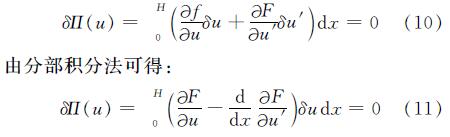
由于古建筑木结构底层柱底一般置于高台基中磉墩之上,有很大的摩擦力,因此边界条件取为

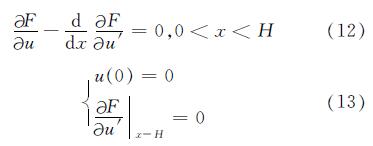
将式(9)对u、u'进行求导后并代入式(12)中,可得:

u(x)=-(f_sq(x))/(6GA_i)x²+Cx+D(14)

根据底部弯矩相等或结构底部剪力相等的原则将水平随机激励荷载简化成三角形分布荷载形式,设等效静力荷载最大值为q,将边界条件(13)式代入(14)式可得木结构侧移曲线.

u(x)=-(μ²_sq)/(6GA_iH)x³+(μ²_sqH)/(2GA_i)x=

(μ²_sqH²)/(6GA_i)[-(x/H)³+3x/H](15)

设木结构在交通激励作用下柱顶水平振动位移为U(x,t),即

U(x,t)=u(x)z(t)(16)

式中:u(x)为结构的水平侧移函数; z(t)为时间的函数.

假设木结构在荷载作用下沿水平方向的振动为简谐运动z(t)=Y₀sinωt,则水平位移和水平速度可分别为^[7]

U(x,t)=Y₀u(x)sinωt(17)

V(x,t)=Y₀u(x)ωcosωt(18)

将(15)式代入(18)式,即可求得木结构柱顶水平振动速度幅值.

V(x,t)=(Y₀μ²_sqH²)/(6GA_i)ω[-(x/H)³+3(x/H)]cosωt(19)

V_max(x)=(Y₀μ²_sqH²)/(6GA_i)ω[-(x/H)³+3(x/H)](20)

为了验证本文推导的木结构控制点速度换算公式,对聊城光岳楼在地面交通荷载作用下进行了实测,并对各控制点及顶层柱顶振动速度进行换算分析.光岳楼位于聊城古城中央由高台基和上部木结构两部分组成,建于1374年.高台基为正四棱台,下底边长34.43 m,上边长31.62 m,高为9.38 m,四面各有一半圆拱门,中心处为十字拱相交形式.拱门面宽5.76 m,直线段高度为2.90 m,矢高为2.88 m.南向拱门两侧又各有一小拱门,与中间拱门相似.敞轩东西朝向,楼梯在高台基的出口处.上部木结构位于高台基中央,如图2所示.光岳楼木结构总共有4层,通过现场实测可知一到四层的层高分别为6.8 m、4.4 m、3.6 m、4.4 m,总高度为21.54 m.

对光岳楼在地面交通荷载作用下实测为连续性测试,光岳楼形状比较规则,结构对称,因此选取了整个结构的1/4进行现场监测,共布置61个测点,其中水平振动47个测点,竖向振动14个测点.每层柱顶都设置有8个传感器,图3所示为一层柱顶测点布置位置图.测试时间段选在中午12:00～14:00,下午5:30～7:30两个时间段.通过对光岳楼的现场监测,获取了大量的实测数据,本文只选取其中一层柱顶50 s的实测数据进行分析,图4所示为一层柱顶的速度时程.在进行数据采集时,由于各种因素的影响,采集的数据与光岳楼的真实振动存在一定偏差.为了消除偏差获得相对比较真实的数据,本文对实测数据进行了消除趋势和数字滤波处理,得出各层柱顶水平振动速度幅值,如表1第一行所示.

图2 光岳楼
Fig.2 Guangyue tower

图3 一层柱顶测点布置图
Fig.3 Measuring points on the frist floor top column

图4 一层柱顶测点2-5 EW向水平速度时程曲线
Fig.4 Velocity time history curve of measuring point 2-5in EW direction

通过现场测试已测得光岳楼在地面交通荷载作用下一层柱顶水平振动速度为V_1max,可通过公式(20)求得顶层柱顶水平振动速度V_4max,由于光岳楼木结构各层柱的等效截面面积相差不大,近似认为A₁≈A₂≈A₃≈A₄,一层和四层的柱顶水平振动速度幅值换算如下.

V₁(6.8,t₁)=(Y₀μ²_sqH²)/(6GA₁)ω[-((6.8)/(21.54))³+3((6.8)/(21.54))]cosωt₁;

V₄(19.2,t₂)=(Y₀μ²_sqH²)/(6GA₄)ω[-((19.2)/(21.54))³+3((19.2)/(21.54))]cosωt₂;

(V_1max(6.8))/(V_4max(19.2))=((Y₀μ²_sqH²)/(6GA₁)ω[-((6.8)/(21.54))³+3((6.8)/(21.54))])/((Y₀μ²_sqH²)/(6GA₄)ω[-((19.2)/(21.54))³+3((19.2)/(21.54))])=(-((6.8)/(21.54))³+3((6.8)/(21.54)))/(-((19.2)/(21.54))³+3((19.2)/(21.54)))=(0.917 3)/(1.965 9);

V_4max(19.2)=(1.965 9)/(0.917 3)V_1max(6.8)

同理,利用式(20)可以计算出二层柱顶、三层柱顶的水平振动速度幅值.通过该换算公式的计算,可以快速的计算出光岳楼木结构顶层柱顶水平振动速度幅值.

以一层柱顶的实测值为换算基数,采用式(20)进行其它各层柱顶水平振动速度幅值换算,其换算结果如表1第二行所示.

表1 实测值与计算值比较
Tab.1 Measured value compared with the theoretical value

由表1可见,光岳楼木结构各层柱顶水平振动速度幅值计算值和实测值相差百分比分别3.9%、12.9%、8.6%,可看出顶层柱顶的水平振动速度幅值实测值和理论值非常接近.同时随着光岳楼木结构层数的增加,其柱顶水平振动速度幅值也相应的增大,其中顶层柱顶水平振动速度幅值最大,符合木结构在车辆荷载作用下的振动响应规律.因此,本文通过速度换算对古建筑木结构柱顶水平振动速度幅值计算是合理的,为古建筑木结构在交通荷载作用下顶层柱顶水平振动速度幅值的精确求解提供参考,同时可以快速的对古建筑木结构进行安全性评估,为古木结构的保护和修缮提供了依据.