基金项目:中国博士后科学基金(2017M621156)
第一作者:张树光(1974-),男,教授,博士生导师,主要从事地下工程和环境岩土工程方面的研究. E-mail:zhangshuguang168@163.com 通信作者:路平平(1990-),女,博士,主要从事地下工程和环境岩土工程方面的研究.E-mail:lupingping222@126.com
(1. 辽宁工程技术大学 土木工程学院,辽宁 阜新 123000; 2. 天津大学 建筑工程学院,天津 300072;3.辽宁省阜新公路路政管理局,辽宁 阜新 123000)
(1.School of Civil Engineering, Liaoning Project Technology University, Liaoning Fuxin 123000,China;2. School of Civil Engineering, Tianjin University, Tianjin 300072, China;
shell shape; single-layer lattice shells; wind field; numerical wind tunnel
DOI: 10.15986j.1006-7930.2019.03.005
应用SST κ-ω湍流模型,采用数值风洞技术对贝壳型单层网壳在不同风向作用下结构表面的风压分布进行了数值模拟,获得了结构表面各分区下的压强系数.把其中具有代表性的分区数值风洞理论值与风洞试验结果进行比较分析,结果对比说明:两者吻合较好,所得到的压强分布系数可以用于工程实际,验证了数值风洞模拟技术的可靠性.事实证明以数值风洞技术来分析复杂结构周围的流场进行预测是可行的.
Predicted the distribution of pressure coefficient on surface of the single-layer lattice shells located in Yujiapu which is in shell shape by numerical wind tunnel method. The SST κ-ω turbulence model was adopted. The pressure coefficient of each subarea was computed to make a comparison with the result from wind tunnel test. It was validated that they were in good agreement with the results derived by experiment and the pressure coefficient distribution could be adopted for the project. the numerical simulation method adopted in this paper could be generalized.
本文对地下高铁站房的贝壳型单层网壳结构进行分析,该站房建筑面积约86 200 m2.车站形式为地下两层、地面一层.地下二层为站台层,由3座岛式站台和6条到发线构成; 地下一层为站厅层,设候车大厅、进出站厅、设备用房及办公用房; 地面层为进站大厅.地上部分为“贝壳”型穹顶采光屋面,结构形式为大跨度空间网格结构.全结构主要杆件均采用曲线钢箱梁,72根箱梁相互交叉连接,编织成一个纵向跨度约142 m,横向跨度约80 m,矢高约24 m的贝壳形穹顶网壳结构,其顶部设置有顶环结构、底部设置有箱型圈梁,对单层网壳顶底端起连接和约束作用.
该结构形体新颖,结构复杂,箱形钢梁相互交叉,在现行《建筑结构荷载规范》[1]( GB50009-2001)中找不到合适的体型系数作为其风荷载值.因此本文利用CFD 技术[2-3]对网壳表面的风压分布进行了数值模拟,对不同风向角下网壳表面风压分布进行分析研究,同时探讨了周围建筑物对网壳周围风场的影响,为工程结构设计的风荷载取值提供必要的指导.
风向角下的风压分布特性进行研究.目前本文选取典型风向角(0°、180°)对站房进行不同常用的湍流模型有标准k-ε模型、RNG k-ε[4]模型、SST κ-ω模型、雷诺应力模型和大涡模拟(Large-Eddy Simulation,LES)等.
LES采用滤波函数,直接模拟大尺寸漩涡,效果最好; 雷诺应力模型次之.由于LES还处在研究阶段,且网格划分要求较高,要达到Kolmogorov尺度,对计算机要求较高,并且对入口边界条件敏感[5],目前应用于土木工程的实际问题还不太现实.基于SST κ-ω湍流物理模型在计算以分离流为主的流场时,精度很好[6],故预采用CFX商用流体软件自带的SST κ-ω模型对高铁站房表面风压分布进行数值风洞模拟,该模型综合了κ-ω模型在近壁区和远场计算的优点,一并增加交叉扩散项,且湍流剪切应力的输送过程在湍流粘性系数的定义中给予了充分考虑,因此,SST κ-ω湍流模型的应用范围变得更为广泛.SST κ-ω湍流模型较传统的k-ε湍流模型要更适用于具有逆压梯度流动或分离流动的计算,因而前者更广泛地应用于大气边界层钝体绕流的计算中.以张量形式表达的SST κ-ω湍流模型的流场输送方程为[7]
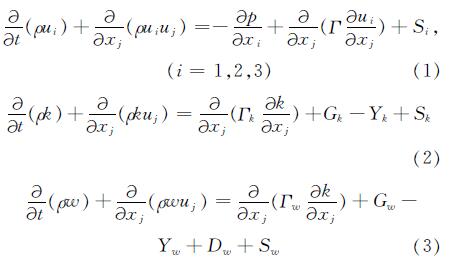
式中:Γ、Γk、Γw为速度u(v或w)、湍动能κ及比耗散率ω的有效扩散系数,(~overG)k、为κ、ω的产生项,Yk、Yw为κ、ω的耗散项,Dw为交叉扩散项,ρ为空气密度,p为压强; Si、Sk及Sw为各输送方程的自定义源项利用有限体积法和SIMPLE[8]压力校正算法来实现非线性离散化方程的解耦和迭代求解,SIMPLE 算法的基本策略是用假定的压强场求解动量方程得到边界点上的通量通过修正假定的压力场反复迭代直至收敛达到求解目的[9].
所建立的数值风洞计算流体域采用862 m*320*192 m[10],网格划分越靠近模型表面单元划分越细.划分网格后节点数为598 793,单元数为3 040 162.
边界条件的入口( inlet)输入平均风速剖面和湍流强度. 根据《建筑结构荷载规范GB 50009-2001》,根据“全国基本风压分布图”,可查得当重现期为100年时天津市地区的风压.由此推算得到基本风速31.6 m/s.根据站房所处的位置,其大气边界层应属D类地区,沿x方向的风速剖面为
V(z)=Vb( z/zb)α,
式中:Vb为标准参考高度处的平均风速(规范取zb= 10 m),α=0.30.z为高度方向,自建筑物底部算起; y、z方向速度为零.
湍流强度I 是地面粗糙度类别和地高度z的函数,鉴于我国规范对湍流强度尚无明确规定,关于I 的表达式,参考日本规范[11-12]取值为
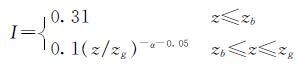
式中:zb取5; zg取450; Ⅲ类地貌α取 0.20.
为进一步验证本文所选湍流模型的优越性,故在相同边界及网格划分条件下,采用不同的湍流模型对实际工程0°风向角进行模拟计算.将各个湍流模型所得结构表面风压系数结果以图表形式列出进行对比.
图7 各湍流模型结果与风洞试验结果对比
Fig.7 Comparison of results getting from each turbulence model and wind tunnel test
量纲为1的压强系数Cp定义为
CP=(P-Pref)
/1/2ρu20
式中:Pref为参考静压力,取为一个大气压0.101 3 MPa; ρ为空气密度,取为1.225 kg/m3; u0为参考风速.
以下分别为风向角为0°、180°时火车站站房网壳的风压系数等值线云图.
当风向角为0°时,如图9由于该结构的流线型造型,在网壳前端出现风压系数较小的正压区,反而是在网壳背部出现较大的正压区,这是该结构与一般结构的不同之处.气流在到达天窗之前出现分离点,在天窗附近负压达到最大,经过天窗之后上部气流与网壳两侧来流在网壳尾部汇集形成较大的正压区,在网壳前端出现正压区,另外网壳两侧气流向中间汇集是网壳前端出现正压区的原因.
当风向角为180°时,由图 10可以看出气流在到达天窗之前出现分离点,在天窗附近负压达到最大,经过天窗之后气流与网壳表面再附着,在网壳前端出现正压区,另外网壳两侧气流向中间汇集也是网壳前端出现正压区的另一原因.
将数值模拟结果与风洞试验结果[14]进行对比进一步验证数值模拟的可靠性.以下分别为数值模拟结果与风洞试验结果的平均风压系数云图的对比.从下图可以看出数值模拟结果与风洞试验结果吻合较好,但是局部细节还是存在较大误差,造成误差的原因可能有:
(1)为建模的方便,在建模时简化了网壳局部的一些细部特征以及风洞试验未考虑天窗影响,所以会造成局部风压系数的误差;
(2)采用的湍流模型包含了湍流的各向同性假设,与实际不符,势必引起误差.这需要将来进一步研究更符合实际的湍流模型如大涡模拟[11],以及不断提高的计算机运算能力来解决;
(3)风洞试验是在大缩尺比的情况下完成,与实际情况存在偏差.
图 11 120°时站房表面压强系数分布(模拟)
Fig.11 Distribution of pressure coefficient on surface of shell with wind angle 120°(numerical simulation)
图 12 120°时站房表面压强系数分布(试验)
Fig.12 Distribution of pressure coefficient on surface of shell with wind angle 120°(experiment)
为研究周围建筑物对结构表面风压的影响,在流体域中分别考虑位于建筑物正前方与正后方的截面尺寸为60 m*60 m*100 m和60 m*60 m*50 m的情况,建筑物与结构的距离分为150 m和75 m两种工况,在各工况下研究在建筑物影响下结构表面风压的影响,图 16为位于结构正前方75 m建筑高度为100 m的流场,可以看出,整个结构位于由于前方建筑扰动形成的漩涡之中,机构表面几乎全为负压,与不考虑周围建筑的情况完全不同,所以在结构的风载设计中要充分结合周围地势与建筑物分布情况,这对结构表面的风压分布将产生决定性作用.图 17为结构后方75 m建筑高度为100 m的流场,可以看出即使建筑物在结构顺风向下方,对结构表面的风压分布亦有很大影响,而所有结构都是出于一定的环境下,确定等效风载是需考虑周围环境的影响.
图 16 50 m高建筑物位于结构前方75 m风场
Fig.16 Wind fields of structure under the condition that 50meter's high building located in front with distance of 75 meters
图 17 100 m高建筑物位于结构前方150 m风场
Fig.17 Wind fields of structure under the condition that 100 meter's high building located in front with distance of 150 meters
图 18 100 m高建筑物位于结构后方75 m风场
Fig.18 Wind fields of structure under the condition that 50meter's high building located in rear with distance of 75 meters
通过工况1与工况2的对比可以发现,建筑物高度对结构表面的风压系数有很大影响.通过工况1与工况4的对比可以发现结构顺风向建筑对风压系数的影响会小于前方建筑,但其影响依然较大不可忽略.
通过对站房网壳结构风场的数值模拟和风洞试验研究,得到相关结论如下:
(1)贝壳型火车站站房网壳结构造型奇特,其周围流场运动比较复杂.采用数值模拟方法对不同风向下站房网壳周边的压强场、速度场以及湍动能场进行了模拟计算.运用数值风洞法对地上网壳部分周围流场进行数值模拟,得到网壳表面的压强系数分布和网壳周围流场的速度分布.
(2)通过风洞试验结果对比,两者吻合较好,验证数值风洞模拟技术的可靠性,但现阶段由于计算机计算能力有限,对湍流的直接模拟方法尚不能有效应用,只能借助湍流简化模型进行计算,造成数值计算结果与风洞试验结果的细节有较大差别,同时风洞试验的大缩尺比也是造成误差的主要原因之一.
(3)由于结构周围环境对结构所受风荷载有很大影响,结构设计阶段应充分考虑最不利工况确定等效风荷载.由于风洞试验的高成本,长周期的弊端,在计算机计算能力充分发展的将来,数值风洞技术可以很好满足工程设计的需要,为结构风载设计提供很好的预测.