基金项目:陕西省自然科学基础研究计划基金项目(2017JM5053); 土木工程防灾国家重点实验室开放基金资助项目(SLDRCE16-04); 国家自然科学基金项目(51408055); 中央高校基本科研业务费资助项目(自然科学类)(300102288106)
第一作者:廖芳芳(1983-),女,副教授,博士后,主要从事钢结构教学和科研工作.E-mail: fangfangliao@chd.edu.cn
<
(长安大学 建筑工程学院,陕西 西安 710061)
(School of Civil Engineering,Chang'an University, Xi'an 710061, China)
Q460D high strength steel; ER55-G welding material; GTN model; parameter calibration; fracture prediction
DOI: 10.15986/j.1006-7930.2019.010.013
分别对取自Q460D高强钢及对应的ER55-G型焊材的9个光滑圆棒试件和18个圆周平滑槽口试件进行单向拉伸试验,获得基本的力学性能参数、荷载—位移曲线和真实的应力—应变曲线.并通过对18个圆周平滑槽口试件的有限元模拟结果与试验数据进行对比,标定得到Q460D高强钢材及对应的ER55-G型焊材的GTN损伤模型参数.利用标定的GTN模型损伤参数对在Q460D高强钢及对应的ER55-G型焊材取材的圆棒试件的断裂点进行预测,验证所标定参数的准确性.并进一步分析初始微孔洞体积比f0、临界微孔洞体积比fc、最大微孔洞体积比fF和形核孔洞体积分数fN四个损伤参数对断裂预测结果的影响.
The monotonic loading tests were carried out on nine smooth round bars and eighteen circumferentially smooth-notched bar specimens of Q460D high strength steel and the corresponding ER55-G welding material to obtain the basic mechanical properties, load-displacement curves and true stress-strain curves. The GTN model parameters of Q460D high strength steel and the corresponding ER55-G welding material were calibrated according to the experimental and finite element analysis results of eighteen circumferentially smooth-notched bar specimens subjected to monotonic loading. Moreover, the calibrated GTN damage parameters were used to forecast the fracture points of coupon specimens of Q460D high strength steel and the corresponding ER55-G welding material, so as to verify the accuracy of the calibrated parameters. Furthermore, the influences of four damage parameters, including initial void volume fraction f0, critical void volume fraction fc, final failure void volume fraction fF and nucleating volume fraction fN, on fracture prediction results were further analyzed.
近年来,随着更多大空间、大跨度、超高层建筑结构和桥梁结构的建设,高强度钢材的应用越来越普遍[1].然而,由于化学成分和内部晶相组织及冶炼和轧制工艺的不同,导致高强钢材的力学性能和断裂性能与普通钢材相比也不尽相同[2].目前对高强钢材的基本力学性能[3]及构件承载能力[4]的研究已经较为成熟,但对于高强钢材的断裂问题研究仍然以传统的断裂力学方法为主,如应力场强度理论、J积分理论和裂纹尖端张开位移(CTOD)理论等,其主要针对含初始缺陷的材料中裂纹开始扩展的条件和扩展规律的脆性断裂问题进行分析[5],而对地震作用下构造无明显缺陷的部位且发生较大屈服变形的韧性断裂问题并不适用[6].
对于韧性断裂问题,Gurson-Tvergaard-Needleman(GTN)细观损伤力学模型[7]从细观的层面对裂纹的萌生和扩展机理进行研究,以微孔洞体积比来反映材料内部微小缺陷的发展变化,结合连续介质力学的方法,定量描述微孔洞扩展同宏观塑性变形的关系[8],而且,ABAQUS等有限元软件已将GTN模型嵌入到材料的本构关系中,是目前国内外用来分析金属材料微观损伤本构模型应用最为广泛地一种方法.但由于GTN模型中有多达9个参数需要分析,对于我国国产Q460D高强钢材及相应的焊材目前尚无研究对其参数进行标定.因此,本文以Q460D高强钢及对应的ER55-G型焊材为研究对象,基于材性试验和圆周平滑槽口圆棒试件的单向拉伸试验及有限元分析,标定了Q460D高强钢及对应的ER55-G型焊材的 GTN 模型参数,并分析了各损伤参数对GTN 模型断裂预测结果的影响.
对于多孔塑性金属材料,GTN模型的屈服函数[9]为
Φ=(σ2e)/(σ^-2)+2q1f*cosh((3q2σm)/(2σ^-))-[1+q3(f*)2](1)
式中: σ^-为材料的等效应力; σe为材料的 Mises等效应力; σm为材料的静水应力,σm=(σ11+σ22+σ33)/3; Tvergaard等[7]采用q1、q2 和q3描述相邻微孔洞间相互作用的损伤修正系数,其中:q3=q12; f为微孔洞体积比,它是微孔洞体积占整个材料体积的比例; f*为损伤变量; f*是孔洞体积分数f的函数,当f*=0时,表示材料损伤尚未发生.f*与f的关系如下:
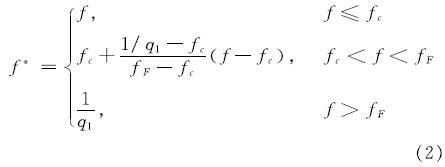
式中:fc为微孔洞聚合时的临界微孔洞体积比; fF为最大微孔洞体积比,当f达到fF时,材料的承载能力完全丧失.微孔洞体积比f的增大可分为两部分,分别为原孔洞的变大fg和新孔洞的形核fn.
df=dfg+dfn(3)
由于基体不可压缩,所以
dfg=(1-df)dεpkk(4)
式中,εpkk为为塑性应变张量的线应变.
对于新孔洞的形核部分,按照应变控制的形核准则和正态分布假设可知:
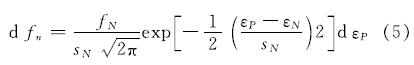
式中:εP为基体材料的等效塑性应变; fN为形核孔洞体积分数; εN、sN分别为孔洞形核时的平均等效塑性应变和标准差.
因此,要建立金属材料GTN 损伤模型,除要确定材料的基本的性能参数外,还需要标定q1、q2、q3、εN、sN、f0(初始微孔洞体积比)、fc、fF和fN等参数.
为了标定GTN损伤模型中的参数,本文主要对取自Q460D高强钢材及对应的ER55-G型焊材的光滑圆棒和圆周平滑槽口圆棒试件进行单向拉伸试验[10],其中Q460D高强钢试件取自一块36 mm厚的低合金钢板,如图1所示,ER55-G型焊材试件是从预制好的Q460D高强钢板对接焊缝上抽取、制作而成的,ER55-G型焊材试件有两种取样方式:一是沿焊缝长度方向取样(本文计为ER55-G1型焊材),二是垂直于焊缝长度方向取样(本文计为ER55-G2型焊材)如图2所示.表1为本批材料的主要化学成分.
试件制作符合《金属材料拉伸试验》(GB/T228.1-2010)的要求,光滑圆棒和圆周平滑槽口圆棒试件的几何尺寸如图3所示,实物见图4.
光滑圆棒试件有效区直径为12.5 mm,分别在Q460D高强钢材、沿ER55-G型焊材的焊缝长度方向及垂直于ER55-G型焊材的焊缝长度方向各抽取3个试件,共计9个试件,试件的编号和尺寸如表2所示.按照图2所示的方式分别在Q460D高强钢及对应的ER55-G型焊材中沿焊缝长度方向和垂直于焊缝长度方向抽取试件,为考察应力三轴度的影响,取三种不同的槽口半径R分别1.5 mm、3.125 mm、6.25 mm,以对应三种不同的应力三轴度,每种材料的每种槽口半径各取2个试件,共18个圆周平滑槽口圆棒试件.表3为圆周平滑槽口圆棒试件的编号及尺寸.为获取Q460D高强钢及对应的ER55-G型焊材的全应力应变曲线.对取自不同材料的9个光滑圆棒试件进行单向拉伸试验,本文试验均在通过单向拉伸试验得到的数据是假设截面面积保持不变的情况下的名义应力σnom和名义应变εnom,由于试件在达到极限强度后截面面积开始缩小,名义应力σnom和名义应变εnom已不再适用.为准确地反映试件的应力应变关系,我们将试验得MTS809疲劳试验机上完成,试验过程中通过50 mm的引伸计控制位移加载.
Q460D高强钢材和ER55-G型焊材各试件的屈服强度σy、极限强度σu、弹性模量E见表4.
通过单向位伸试验得到的数据是假设截面面积保持不变的情况下的名义应力σnom和名义应变εnom,由于试件在达到极限温度截面面积开始缩小.名义应力σnom和名义应变εnom已不再适用。为准确地反映试件的应力应变关系.我们将试验得到的名义应力σnom和名义应变εnom利用公式(6)换算为真实应力σtrue和真实应变εtrue.
εtrue=ln(1+εnom)(6)
σtrue=σnom(1+εnom)(7)
试验过程中只记录了在摘除引伸计之前的应力应变曲线,但是,摘除引伸计后试件仍将产生较大的变形直至试件发生断裂,而在进行有限元分析时,需要输入从材料屈服至断裂时刻的真实应力 - 塑性应变数据.因此在单向拉伸试件发生断裂后,还需测量断裂时刻试件所受的力及试件在断裂处截面的直径,通过公式(8)、(9)计算试件断裂时刻的真实应力σfracturetrue和应变εfracturetrue,结果见表5.
σfracturetrue=(Ffracture)/(πd2f/4)(8)
εfracturetrue=ln[((d0)/(df))2](9)
式中:d0为试件标距段的初始直径; df为试件断裂后测得的断裂处的直径.
图5给出了Q460D高强钢及对应的ER55-G型焊材从材料屈服至断裂时刻的真实应力 - 塑性应变数据.
对上述不同材料不同槽口半径的18个圆周平滑槽口圆棒试件进行单向拉伸试验,试验加载装置与光滑圆棒单向拉伸试件相同.图6为试验现场照片.
通过对Q460D高强钢圆周平滑槽口试件的单向拉伸试验,可以得到试件的力 - 变形曲线,如图7所示,其他的材料试件的力 - 变形曲线与之类似,在图7所示的各条力 - 变形曲线的下降阶段均存在一个斜率突变点,在分析时,我们将该作点为试件延性裂纹开展的点,使其与GTN损伤模型对钢材及焊材裂纹开展的预测结果进行对比,来检验GTN模型的预测能力,并进行材料损伤参数的识别.图8为部分拉断的试件,其他试件与之类似.
图7 Q460D高强钢圆周平滑槽口圆棒试件单向拉伸试验结果
Fig.7 Unidirectional tensile test results of smooth- notched coupon specimens of Q460D high strength steel
由于GTN 模型中的微孔洞体积分数很难由试验直接确定,因此需将试验所得到的荷载—变形曲线同基于GTN模型的ABAQUS有限元模拟结果进行对比,通过调整待定参数,使得两条曲线无限贴合,所输入的损伤参数即为材料的GTN模型损伤参数.
采用 ABAQUS 软件对每一个圆周平滑槽口圆棒试件建立有限元模型,应用软件中嵌入的GTN损伤模型对试件进行分析,模型如图9所示,采用CAX4R单元(4节点四边形、轴对称、减缩积分),为得到更加准确有限元分析结果,对开槽口处网格进行加密.
对于GTN模型中,为考虑微孔洞间的相互作用而引进的参数q1、q2 和q3,本文根据Tvergaard等[7] 研究成果,取q1=1. 5,q2=1,q3=q21=2.25.
对于形核孔洞体积分数fN、孔洞形核时的平均值εN、和标准差sN,Chun等[11]在大量试验研究的基础上,提出εN=0.3、sN=0.1 适用于大多数的钢材,目前已被大量学者引用,且取得了很好的钢材断裂预测效果.Corigliano等[12]指出钢材fN的极限值在0~0.1之间.其具体值可通过试验获得的荷载 - 位移曲线与有限元分析的结果进行对比,采用逆向法的思路反推得到[13].
对于微孔洞聚合时的临界微孔洞体积比fc、初始微孔洞体积比f0和最大微孔洞体积比fF.Sun等[14]认为fc是常数,可以通过与光滑圆棒试件单向拉伸的试验结果进行对比分析,从而确定其值.Gao等[15]通过大量实验研究表明:对于大多数C-Mn钢,初始微孔洞体积比f0可取0.002 5,Q460D高强钢材的主要化学成分为C和Mn,因此本文取f0=0.002 5作为Q460D高强钢的初始微孔洞体积比.而对于ER55-G型焊材,本文参考Zhang等[16]的研究结果取f0=0.005.Brown等[17]的研究发现,fF=0.25 适用于大多数金属材料,但黄学伟等[9]通过对Q690D高强钢材的试验研究及与有限元结果进行拟合,认为fF=0.17更适合于Q690D高强钢材,本文借鉴其研究成果,对Q460D高强钢及ER55-G型焊材均取fF=0.17,且通过试验研究与有限元分析验证了取值正确性.
综上,本文需通过试验标定GTN模型中的fN、fc和fF三个参数值.最终标定的Q460D高强钢及ER55-G型焊材的GTN模型参数列入表6中,图 10 为采用表6参数对取自Q460D高强钢及ER55-G型焊材的18个平滑槽口试件进行断裂预测结果与实测数据的对比.可以看出:采用GTN损伤模型的有限元分析结果与试验曲线吻合良好,说明表6中的所标定的GTN模型参数可以准确预测圆周平滑槽口试件的断裂行为.
表6 Q460D高强钢及对应的ER55-G型焊材的GTN模型损伤参数
Tab.6 GTN damage parameters of Q460D high strength steel and the corresponding ER55-G welding material
由表6可以看出,其中Q460D高强钢材与ER55-G型焊材的损伤参数以及不同取材方向的焊材之间的损伤参数均有所不同,主要通过初始微孔洞体积比f0和形核孔洞体积分数fN来体现.从细观的层面分析,对于初始微孔洞体积比f0,ER55-G型焊材大于Q460D高强钢材的原因是受加工工艺和焊接环境的影响,ER55-G型焊材基体中所含的夹杂物要比Q460D高强钢材多,这导致ER55-G型焊材的初始微孔洞多于Q460D高强钢材,体现在宏观上即为f0(ER55-G)>f0(Q460D).对于形核孔洞体积分数fN,West[18]研究表明:空洞第二相粒子的形核和界面的微观特征并没有直接的联系,目前仅可通过试验和有限元模拟结果进行对比采用逆向法进行确定,其具体的影响因素还有待研究.
如图 11是以ER2-9试件为例,其他参数均按上述标定参数,分别取f0为0.0025、0.0050、0.0075时的荷载 - 位移曲线,明显可以看出,在其他参数确定的情况下,初始微孔洞体积比f0主要影响试件的断裂点,f0的值越大断裂点越靠前.
图 11 f0取值不同时试件ER2-9的荷载 - 位移曲线
Fig.11 Load-displacement curves of specimen ER2-9 with different f0
当材料内部出现微小裂纹后,参数fc起主要控制作用,图 12为其他参数一定时,fc分别取0.05、0.10、0.15时的荷载 - 位移曲线,可以看出,fc取值越小,材料的最大孔隙率越易达到临界孔隙率fc,体现在图中即为材料的断裂点越靠前,材料越容易失效.
图 12 fc取值不同时试件ER2-9的荷载 - 位移曲线
Fig.12 Load-displacement curves of specimen ER2-9 with different fc
对取自Q460D高强钢及对应的ER55-G型焊材的9个光滑圆棒试件及18个圆周平滑槽口试件进行了单向拉伸试验,并对18个圆周平滑槽口试件进行了有限元分析,标定了Q460D高强钢材及不同方向取材ER55-G型焊材的GTN损伤模型参数,分析了f0、fc、fF 和fN损伤参数对 GTN 损伤模型断裂预测结果的影响.得到以下结论:
(1)Q460D高强钢与ER55-G型焊材的GTN损伤参数有所不同,主要通过在初始微孔洞体积比f0和形核孔洞体积分数fN来体现.
(2)对于ER55-G型焊材,加载方向影响GTN损伤模型中形核孔洞体积分数fN.
(3)GTN损伤模型中f0、fc、fN均对预测结果中试件的断裂点有影响,f0、fN越大,断裂点的位置越提前,但fN对断裂点位置影响更大.而fc对于断裂点的影响恰恰相反,fc越大,断裂点的位置越提前.fF对断裂预测结果的影响主要体现在对断裂后承载力的下降速度的影响,fF越小,承载力下降越快.
(4)通过将本文所标定的损伤参数代入GTN损伤模型中与试验结果进行对比发现,本文所标定的损伤参数能够较准确预测试件的断裂行为.