基金项目:重庆市教育委员会科学技术研究计划青年项目(KJQN201804303); 重庆市建设科技计划项目(城科字2018第(2-42)号)
第一作者:梁莉(1976-),女,硕士,副教授,主要从事道路工程方面的教学和研究工作.E-mail: lila76@sina.com 通讯作者:文锦(1990-),男,硕士,高工,主要从事与岩土工程和道路工程相关的研究工作.E-mail: 568381682@qq.com
(1.重庆建筑工程职业学院 轨道与机电工程系,重庆 400072; 2.重庆大学 土木工程学院,重庆 400045; 3.中国中铁二院昆明勘察设计研究院有限责任公司,云南 昆明 650200; 4. 中匠民大国际工程设计有限公司,四川 成都 610094)
(1.Department of Track and Electromechanical Engineering, Chongqing Jianzhu College, Chongqing 400072, China;2. School of Civil Engineering, Chongqing University, Chongqing 400045, China; 3. Kunming Survey, Design and Research Institute Co. Ltd., China Railway Eryuan Engineering Group Co. Ltd.(CREEC), Kunming 650200, China; 4. China Craftsmen International Engineering Design Co. Ltd., Chengdu 610094,China)
traffic loading; buried pipeline; mechanical characteristics; 3-dimensional
DOI: 10.15986/j.1006-7930.2020.01.010
针对埋地PE管道采用ANSYS商业软件建立了移动恒定荷载作用下三维力学模型,基于新建模型监测了行车荷载作用过程中埋地管道关键位置处竖向位移以及Mises应力的时程响应,分析了移动恒定荷载作用下车行道下方埋地柔性管道的力学性状以及不同结构层的力学性状.研究结果表明:(1)管道纵向上最大力学响应出现在行车荷载作用点正下方的管道顶部,任意横截面上,竖向位移以及Mises应力的最大值均位于管道顶部;(2)监测点与荷载作用点间距离越小,管道监测点处的力学响应越大;(3)管道纵向长度方向上管顶的竖向位移和Mises应力的最大值出现在道路两端,管道中间部位最大力学性状差别不大;(4)埋深较浅的结构层受移动荷载影响程度较大,随着埋深增加,受影响程度快速降低.
ANSYS commercial software is adopted to construct a 3D mechanical model to simulate deformation and stress state of buried PE pipes under traffic load. The time-procedure response of vertical displacement and Mises stress at the key position of buried pipes are monitored during the loading process based on the newly constructed model. The mechanical responses of buried pipes beneath the roadway and different structural layers are analyzed. These results indicate that:(1)The most obvious mechanical response along the longitudinal direction of pipes takes place at spots under load points. On arbitrary cross-section, the vertical displacement and Mises stress arrive at the maximum at the top of the pipe.(2)The smaller the distance between monitor points and load points, the greater the mechanical response at monitor points.(3)Maximum vertical displacement and Mises stress take place at the end of the pipe, and there is no distinct difference between mechanical characteristics of points in the middle part of the pipe.(4)Traveling constant loading has a great influence on the deformation of shallow buried structural layers, and an increase in burial depth leads to a decline in the degree of influence.
聚乙烯管(PE管)因其耐腐蚀、连接可靠、管材廉价和施工方便等卓越性能,在当前的管道运输当中发挥着重要的作用[1].对于车行道下方埋地管道在频繁的外荷载作用以及PE管自身的老化作用下,管道的破坏现象普遍存在.交通荷载是最主要且最频繁的动荷载之一,研究交通荷载作用下埋地管道的三维力学性状是揭示管道致灾机理的有效手段之一[2].
真实的交通荷载是动荷载,其大小、方向以及作用点随时间不断变化,由于模型的复杂性往往在理论及数值计算上会遇到很大的困难[3].为了简化计算,通常采用的计算模型包括静力荷载模型、均布恒载模型、移动恒载模型、振动荷载模型、冲击荷载模型等确定性模型[4].董冬冬等[5]将路面交通荷载简化为作用在土基顶面的竖向均布荷载,由此研究了交通荷载作用下埋地HDPE管道附加弯矩的影响因素及变化规律.李新亮等[6]应用线弹性理论,采用静力计算方法分析了车辆荷载作用下埋地管道的应力问题.赵龙飞等[7]利用静载和冲击荷载模型模拟了交通荷载,并对埋地管道的变形特性进行了三维仿真计算分析.对于管路交叉情况只提出了稳态荷载模型,并未进行实际的模拟计算.李洵等[8]采用了长期均布荷载、移动恒载和稳态简谐荷载三种模型,分析了管道的Mises应力和竖向位移.但是其研究对象仍是传统的刚性管材,其研究结果对于柔性埋地管并不完全适用.实际上,相比于刚性埋地管道,柔性埋地管道在受管周土传递的有效应力变形后会对管周土体产生更显著的挤压,反之受挤压的管周土会对埋地管身产生更大的弹性抗力,进而约束管材进一步的变形.简单地,管周土对于管体既是荷载也是约束,管—土之间存在着相互作用与变形协调.因此交通荷载作用下考虑管—土相互作用的柔性管道的力学性状分析得到越来越多的关注[9-10].
回顾以往文献,对于交通荷载作用下埋地管道的研究,多数研究采用静态荷载模型,研究对象也多为钢管和混凝土管等刚性管道.大部分的研究成果也忽略了管 - 土相互作用对埋地柔性管道力学特性的影响.难以全面揭示交通荷载作用下管道的力学性状.
本文运用了ANSYS有限元分析软件,针对埋地柔性PE管道建立移动恒定荷载作用下埋地柔性管道的三维动态力学计算模型,详细地探讨了行车荷载作用下车行道下方埋地管道的受力特性和变形性能.研究成果对于埋地管道的设计、施工以及检修具有一定的工程参考价值.
根据国家《城市道路设计规范》[11]的有关规定,取小型车专用车道为研究对象,车道为双向4车道,设计车速为40 km/h,道宽为3.25 m,总宽为13 m,管道埋深为2 m.在保证计算精度的同时,经多次试算,模型尺寸确定为13 m×6 m×4 m.
由于管周土体往往是层状结构,各层的力学性能差异很大,因此本文选择层状路基模型,各层厚度以及名称如图1所示.交通荷载为平行于管道纵向且作用点与管道中点位于同一个竖直平面内的单个轮压荷载.
利用ANSYS商业软件进行三维建模,埋地PE管道采用solid185三维八节点实体结构单元,其余结构采用solid45三维实体结构单元.本研究重点在于讨论管道的力学性状,综合平衡计算速率以及计算精度后,管道以及管周土体部分网格划分较为紧密,其余部分网格划分较为稀疏.具体的模型网格划分情况如图2所示.填土以及岩石硬基设置为D-P本构模型,由于研究重点是管体以及管道一定范围内的管周土,同时路面结构距离研究区域较远且厚度相对较小,因此为了简化计算,路面结构层的本构模型设置为线弹性.为了合理地确定材料力学参数,本研究借鉴了相关文献[12-15],道路模型各层及管道计算参数取值如表1.
车轮与道路的接触面实际上可近似为椭圆面,如图3(a)所示.为了便于行车荷载的计算以及施加,将实际的椭圆接触面简化为当量矩形接触面,如图3(b)所示,且假定车辆荷载在当量矩形接触面上均匀分布.
根据规范[11],单个车轮接地面实际上为一个0.4L×0.6L的矩形和两个半径为0.3L的半圆的组合面,且接触面面积积按下式:
A1=0.4L×0.6L+π(0.3L)2(1)
如图3(b)所示,根据面积A1=A2可得当量矩形长度.
L0=(A1)/(0.6L)(2)
根据规范[16]取胎压为Ps=0.7 MPa,取单轴标准轴载F为100 kN.此时,有
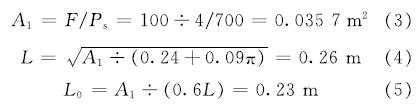
所以,轮胎接地面积简化为0.23 m×0.156 m的矩形.
管道结构和管周土体相互作用是典型的接触非线性问题,二者之间除了传递压力之外,还存在摩擦力以及相对位移.将管、土接触处抽象作为面 - 面接触,管道为接触面,由contact174三维八节点的面 - 面接触单元组成,土体为目标面,由target179三维目标单元组成.考虑到动摩擦效应,由表1知土基为压实土,所以,管、土间的摩擦系数取0.18[14].
模型的交通荷载作用方式为移动恒载,荷载移动方向(行车方向)与管道纵向方向一致且荷载作用点与管道中心线位于同一竖直平面内.采用阶跃加载的方式在顶面中按当量矩形面积划分的网格上施加面荷载.具体的荷载施加方式为,从边界单元开始,选择一组单元施加面荷载F,持续时间t,采用完全瞬态动力分析方法进行求解分析,随后沿着行车方向逐步改变面荷载的作用位置,依次进行力学求解分析,同时记录监测点的力学特征变化.对于移动恒载,考虑每一组单元的面荷载F和持续时间t随作用点位置的变化,可以实现车速以及车重对埋地管道力学特性的影响的研究.为了简化计算模型,本研究中面荷载F以及持续时间t在行车过程中均保持不变.结合埋地管道实际约束条件,设置模型顶面为自由边界,设置模型底面为固定约束,模型其余各面设置为粘弹性动力人工边界.
本文的目的是揭示行车过程中埋地柔性管道的纵向力学响应以及各结构层的力学响应,为了便于分析,首先假定行车荷载作用于沿管道纵向四分之一处和道路中点处以揭示埋地管道纵向力学特性一般规律,然后固定沿管道纵向四分之一处和道路中点处的监测点改变荷载作用位置以揭示行车过程中某一固定点的力学性状时程响应,最后揭示了移动荷载过程中不同结构层的力学响应.荷载施加以及监测点位置设置情况如图4所示.为了直观地确定模型中的最危险区域,选取Mises应力σ4来度量管道的应力状态[15].

以管道的竖向位移为指标来度量其变形程度.
当车辆荷载作用于沿管道纵向四分之一处,管道纵向前部靠近荷载作用点附近发生明显纵向位移以及Mises应力.在埋地管道任意横截面上,位移呈梯度分布,最小竖向位移出现在管道底部,最大竖向位移出现在管道顶部,Mises应力出现在管道外表面顶部,最小等效应力位于管道内表面管腰附近.在管道纵向上,竖向位移以及Mises应力的最大值均位于车辆荷载作用点处正下方的管道顶部.
当车辆行驶至道路中点时,在管道纵向上管道结构的竖向位移和Mises应力均以管道中截面对称分布,与车辆荷载作用于道路长度1/4位置处相似的是,最大的等效应力以及竖向位移仍然位于车辆荷载作用点处正下方的管顶外表面.李新亮等[6]在分析交通荷载作用下埋地管道的应力状态时也观察到了相似的一般规律.
为了更进一步地定量分析移动恒载作用下埋地柔性管道的力学性状,分别选取管道1/4以及1/2长度处的管顶为监测点,图5(a)、图5(b)、图5(c)、图5(d)分别展示了监测点在移动恒载作用下的竖向位移以及Mises应力的时程响应.
当荷载位于道路起点与1/4管道长度间,1/4道路长度处管顶的竖向位移和Mises应力随着荷载向前移动逐渐增加; 当荷载位于1/4道路长度与道路末端间,1/4道路长度处管顶的竖向位移和Mises应力随着荷载向前移动逐渐减小且趋于平缓; 当荷载达到1/4路面位置时,管顶竖向位移和Mises应力均达到最大值.
在移动恒载作用下,1/2道路长度处管顶竖向位移与车辆荷载位置关系呈向下抛物线关系并且关于道路中心对称分布,因此只分析曲线的左半部分.当车辆荷载位置小于2.5 m时,管顶竖向位移随车辆荷载位置的增加而增加,且增加速率较小.当车辆荷载位置介于2.5 m与6 m间,增长速率较大.当荷载达到道路中点时,竖向位移达到最大值.与位移的分布规律相同,管顶Mises应力的时程分布也呈抛物线形.在移动恒载作用下,在道路起点与道路中点间,管顶Mises应力随着车辆荷载位置的增大而增大,其中在车辆荷载位置达到2.5 m后,增长速率明显变大.当车辆荷载到达管道正上方时Mises应力达到最大.由此可见,显著影响管道中点力学性状的车辆荷载位置位于2.5 m与9.5 m之间.周敏等[17]在对埋地HDPE管道地层沉陷过程中管道力学行为研究过程中,也发现了相似的规律.前述研究表明了,在任何状态下,在管道纵向方向上,管道的最大力学响应均发生在荷载作用点处的正下方.不同荷载作用点处,最大力学响应肯定也有所不同.图6(a)、图6(b)分别展示了,车辆荷载移动过程中,管道纵向上管顶竖向位移和Mises应力最大值的时程响应.
恒定荷载移动过程中,管顶竖向位移和Mises应力的时程变化曲线均关于管道中点对称,且最大值均出现在管道两侧端.恒定荷载在管道纵向4~8 m范围移动时,管顶竖向位移和Mises应力的最大值出现在管道中点,但相比于其他位置差别很小.由此可见,当行车荷载位于道路端部埋地柔性管道的力学性状最为强烈,为了避免埋地管道的破坏,应加强对埋地管道的端部的保护.为了研究移动恒载作用下,道路下方不同深度处结构层的竖向位移和竖向应力的时程响应.分别在道路中点下方不同结构层顶面处设置监测点,记录行车过程中各监测点的力学性状.图7(a)、图7(b)分别展示了不同结构层的竖向位移和竖向应力的时程变化.
从图7(a)可以看出,移动恒载作用下,明显影响不同结构层处竖向位移的车辆荷载位置范围较大,不同结构层顶面竖向位移随车辆荷载位置变化趋势大致相同.车辆荷载位置与不同结构层顶面的竖向位移间关系均呈抛物线分布,与荷载作用点距离越远,竖向位移均越小.任意车辆荷载位置处,随着深度的增加,竖向位移逐渐减小,并且下降速率随深度增加而增加.移动恒载对竖向应力的影响与竖向位移有所不同.针对图7(b)的分析表明,深度较浅的沥青面层、水泥稳定碎石层和填土顶面,其竖向应力变化受移动恒载的作用范围比较集中,且竖向应力变化幅度较大,竖向应力主要为压应力.当荷载作用位置离道路中点较远时,受到向上的拉应力.各点竖向应力均在移动恒载作用于道路中点时达到最大,随着深度的增加,竖向应力逐渐减小,并且衰减速率随深度而增大.移动恒载对位于地面以下2 m深度处的管顶的竖向应力影响较小.
为了分析车行道下方埋地柔性管道在交通荷载作用下的三维力学性状,以高密度聚乙烯PE管材为对象,将交通荷载简化为移动恒定荷载,采用ANSYS有限元计算软件建立埋地管道—管周土三维接触耦合模型,模拟了移动恒荷作用下管道的受力特征,得出了以下结论:
(1)行车过程中,埋地管道的最大力学响应发生在荷载作用点正下方的管道顶部; 埋地管道任意观测点处的力学响应随着与荷载作用点距离的增大逐渐减小.
(2)恒定荷载移动过程中,管道全长上竖向位移和Mises应力最大值的时程变化曲线均关于管道中点对称,且最大值均出现在管道两侧端,应加强对道路端部埋地管道的保护.
(3)移动恒载作用下,影响不同结构层处竖向位移的荷载范围较大,埋深越浅受移动恒载影响程度越高; 深度较浅的结构层其竖向应力变化受移动恒荷的作用范围比较集中,且竖向应力变化幅度较大,竖向应力主要为压应力,随着作用点的远离,地面可能出现拉应力; 埋深较大的结构层的竖向应力受荷载移动影响较小.