基金项目:国家自然科学基金项目面上项目(51678115)
第一作者:黄丽华(1967-),女,工学硕士,教授,从事薄壁构件的稳定性研究.E-mail:lhhang@dlut.edu.cn
(Faculty of Infrastructure Engineering, Dalian University of Technology, Dalian 116024, China)
Cold-formed thin-walled steel; axial compression capacity; effective width method; direct strength method; channel section
DOI: 10.15986/j.1006-7930.2020.02.004
在各国轻钢结构设计规范中,冷弯薄壁型钢轴压承载力的计算主要基于有效宽度法和直接强度法.本文通过研究美国钢铁协会(AISI)规范和中国冷弯钢规范(GB 50018—2014征求意见稿)中有效宽度法和直接强度法的计算公式,以76根常规槽形截面试验杆件为对象,对比基于不同计算方法得到的轴压承载力,分析两国规范中基于两种算法计算结果的精度、可靠性和差异性.计算结果表明:中国规范(意见稿)的直接强度法和美国规范的有效宽度法计算结果和试件试验承载力更接近,中国规范(意见稿)的有效宽度法的计算结果偏保守,而美国规范的直接强度法计算的承载力偏危险且离散性最大.
In the light steel structure design codes of various countries, the calculation of the axially buckling loads of cold-formed thin-walled steel members is mainly based on the effective width method and direct strength method. In this paper, through the study of the formulas in American Iron and Steel Institute(AISI)and the Chinese Cold-formed Steel Specification(GB 50018—2014 draft), 76 specimens of regular channel sections are taken as the objects, the comparison of axially buckling loads obtained from the different calculation methods with the experiment results was conducted. The accuracy, reliability and the differences of calculation results based on the algorithms in the two countries' specifications are analyzed. Results show that the calculation results of the direct strength method in the Chinese code(draft)and the effective width method in the American code are closer to the bearing capacity of the specimens. The calculation results of the effective width method in the Chinese code(draft)are conservative, while the calculation results of the direct strength method in the American code are dangerous and discrete.
目前在多数国家的冷弯钢规范中,稳定承载力的设计方法主要是基于有效宽度法和直接强度法建立的.有效宽度法是通过折减构件截面的面积来考虑板件发生局部屈曲对构件整体承载力的降低作用.有效宽度法经过几十年的发展,相关设计理论已经比较完备,可以计算各种受力形式和边界条件的简单截面板件.但随着构件截面越发的轻薄、复杂,板件的屈曲系数求解也愈发复杂,导致板件截面的有效特性计算繁琐或难以计算,阻碍了新型截面形式构件的发展.此外,由于截面板件弯折成各种复杂加劲形式后,板件的局部稳定性有很大提高,然而这种薄壁高强截面构件易出现另一种更复杂的屈曲模式—畸变屈曲[1].畸变屈曲是区别于局部屈曲和整体屈曲的新屈曲形式[2],其性能不同于一般的局部屈曲,很难用有效宽度法进行计算.而直接强度法可以很好地解决有效宽度法的不足,作为一种新兴设计方法,直接强度法是通过折减构件强度来考虑板件局部或截面畸变屈曲对构件整体承载力的降低作用,不需要确定截面的有效宽度,使用毛截面计算构件的承载能力,可以方便地计算带有复杂加劲截面的承载能力,有助于新型截面形式的推广和应用.
本文在总结有效宽度和直接强度理论基础上,依据美国钢铁协会(AISI)规范[3]和中国冷弯钢规范(2014)征求意见稿[4],将选取的试件计算结果与试验结果进行对比,为建立合理的冷弯薄壁型钢轴压承载力的设计方法提供参考.
当板件具有较强的侧边支撑时,有时板件屈曲后并不会破坏,还可以继续承担荷载,而且板件宽厚比越大,可发挥的强度潜力越大.对于板件屈曲后强度的利用,1932年冯·卡门[5]首次提出了“有效宽度”的概念,并提出了用于加劲板件设计的计算公式,公式如下:
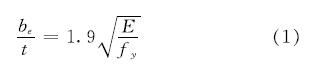
式中:be、t是板件的有效宽度和厚度; E为材料的弹性模量; fy为材料的屈服强度.
1946年Winter教授[6]在大量试验研究的基础上对冯·卡门公式进行了改进,提出了计算沿两纵边简支的板有效宽度计算公式:
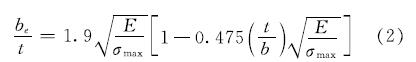
式中:b是板件的宽度; σmax是板件受到的最大应力.
以往的分析方法是基于理论推导,没有对各种复杂因素进行确切的定量描述,式(2)是一个半经验半理论的计算公式,通过引入修正系数,考虑薄壁柱的初始缺陷、残余应力等各种因素的影响,计算结果更接近于实际构件.
1968年T. Pekoz 等人经过长期研究,将Winter 教授的公式一般化,推广为适用于各类板件在各种受力状态的Winter公式,并定义为受压构件有效宽度计算的统一法则[7],这大大拓宽了有效截面法的适用范围,并可以很好的用以指导设计.美国AISI 规范在1996 年修订时采用此公式来计算截面的有效宽度,公式如下:
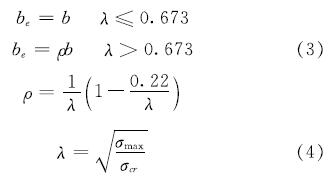
式中:ρ是板件宽度的折减系数; λ是板的柔度系数; σcr是板件的弹性屈曲临界应力,采用经典薄板弹性稳定理论计算,临界应力计算公式为
σcr=(kπ2E)/(12(1-v2)(b/t)2)(5)
式中,k是板件屈曲系数,与板件边界条件、受力和幅面尺寸比值有关.
采用式(3)~(4)计算的板件和构件的极限强度与试验结果比较符合,澳大利亚、欧洲和北美许多国家规范都采用此通式来计算冷弯薄壁型钢板件的有效宽度[8].
中国冷弯型钢规范[9]中板件有效宽度的计算公式不同于国外通用的有效宽度设计公式,但本质也是来源于Winter公式.我国有效宽度计算采用三段式,对加劲板件、部分加劲板件和非加劲板件都适用,详细计算公式参见文献[9].
对有效宽度计算,最核心的是屈曲系数k的计算.对于单向均匀受压的加劲板件和非加劲板件,各国规范根据精确的解析解规定屈曲系数为k=4和0.43; 而单向均匀受压的部分加劲板件由于卷边约束程度不同,会呈现不同的屈曲性能,因此目前还没有统一的解析解.中国现行冷弯钢规范不考虑卷边的约束影响,统一取0.98,但在中国冷弯型钢规范(意见稿)中则考虑了畸变屈曲的影响,不再取定值而是根据公式计算.美国AISI规范在确定均匀受压部分加劲板件稳定系数时,根据边缘加劲板件尺寸分为两种情况计算.
1998年Schafer和Pekoz[10]总结了前人的的研究成果,首次提出了冷弯型钢构件直接强度设计方法,并对其发展做了大量研究工作,通过对17位研究者的574根受弯构件试验数据进行回归分析,得到了受弯构件直接强度设计曲线.2002年,Schafer基于已有梁的研究工作,又把直接强度法引入到柱中,给出了轴压柱直接强度法设计公式[11].
直接强度法是根据构件截面的弹性屈曲性能,通过强度设计曲线来预测构件的极限强度,所以只需要知道构件的屈服应力和弹性临界局部、畸变和整体屈曲应力,再将其代入整个截面直接强度设计公式,就可求得构件的极限强度.整个过程不需要求解构件的有效截面属性,使用构件的毛截面,因此方便进行复杂截面的强度计算,并且考虑了构件发生畸变屈曲变形情况,可以求解畸变屈曲强度.直接强度法作为一种新兴的设计方法目前已被北美、澳洲写入规范作为有效宽度法的替代方法,我国的《冷弯型钢结构技术规范》(征求意见稿2014)[4]也采纳了这一方法.
AISI规范[3]中轴心受压构件直接强度法的计算公式如下:
(1)整体屈曲承载力(Pne):
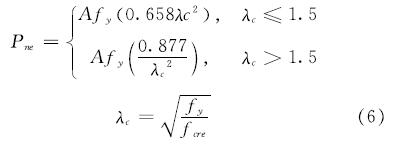
式中:A是构件截面面积; fy是材料的屈服强度; fcre是构件整体屈曲弹性临界应力(取构件弯曲和弯扭屈曲应力的最小值).
(2)畸变屈曲承载力(Pnd):
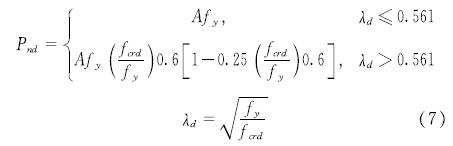
式中,fcrd是截面畸变屈曲弹性临界应力.
(3)局部 - 整体相关屈曲承载力(Pnl):
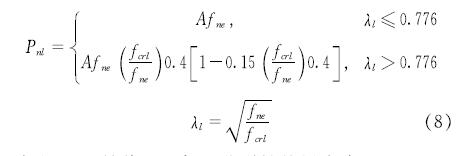
式中,fcrl是截面局部屈曲弹性临界应力.
轴心受压构件的稳定承载力为Pn=min(Pne,Pnl,Pnd).
中国规范(意见稿)[4] 中轴心受压构件直接强度法的计算公式如下:
(1)局部 - 整体相关屈曲承载力(Nnl):
Nnl={Nne, λl≤0.847
[1-0.10((Ncrl)/(Nne))0.36]((Ncrl)/(Nne))0.36Nne, λl>0.847(9)
式中:λl是无量纲长细比,
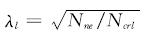
Ncrl是局部屈曲临界荷载,Ncrl=Aσcrl; Nne是构件整体稳定承载力,按下式计算:
Nne=Aφfy(10)
式中:A是全截面面积; fy是钢材的强度标准值; φ是轴心受压构件稳定系数.
(2)畸变与整体相关屈曲承载力(Nnd)
Nnd={Nne λd≤0.561
[1-0.25((Ncrd)/(Nne))0.6]((Ncrd)/(Nne))0.6Nne λd>0.561(11)
式中:λd是无量纲长细比,
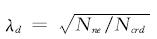
Ncrd是畸变屈曲临界荷载,Ncrd=Aσcrd.
轴心受压构件的承载力为N=min(Nnl,Nnd).
依据美国AISI规范[3]和中国冷弯型钢结构技术规范(征求意见稿2014)[4]中的有效宽度法和直接强度法计算公式,选取文献[12-16]中的76个发生局部、畸变、整体及耦合屈曲的槽形截面轴心受压杆件,分别计算了各杆件的极限承载力并与试验结果对比见表1~表5,篇幅限制,表2~表5只列出最终统计结果.其中采用AISI规范中的直接强度法计算时,使用了广义梁软件GBTUL[17]计算构件均匀受压时的弹性局部和畸变临界屈曲应力; 而中国冷弯钢规范(征求意见稿)中的直接强度法则提供了临界屈曲应力的计算公式.为了更真实反映试验构件的计算值,更好的与试验结果进行比较,规范中的材料强度值统一取各构件通过材性试验得到的屈服强度fy.
综合分析上述计算结果可知,中国有效宽度法的计算结果最保守,对所有试件的计算结果都是最小的,而且离散性偏大,美国有效宽度法与试验数据则拟合的较好,离散程度较好.虽然中国规范(意见稿)[4]中部分加劲板板件屈曲系数的计算考虑了畸变影响,相对现行冷弯钢规范[9]屈曲系数得到了提高,不再统一取0.98,但有些截面翼缘屈曲系数和有效宽度相对美国规范计算值还是明显偏低.依据中国和美国规范计算的部分加劲板件屈曲系数和有效宽度比值随计算系数ρ的关系见图1和图2.从图中可以发现,计算系数ρ偏小时,依据中国规范计算的部分加劲板件有效宽度和屈曲系数要比美国规范计算值小很多.即使有一部分部分加劲板件依据中国规范计算的屈曲系数大于美国规范计算值,但计算的有效宽度仍比美国规范计算值偏小.
表1 文献[12]试件承载力的计算值与试验值对比
Tab.1 Comparison of ultimate loads between the computation and test for specimens in literature [12]
类别 P1/Pt P2/Pt P3/Pt P4/Pt平均值 0.739 0.979 0.933 0.890标准差 0.054 0.058 0.042 0.053
备注:卷边槽钢试件20个
图1 Kf(CN)/Kf(AI)-ρ关系
Fig.1 Relationship between Kf(CN)/Kf(AI)-ρ
图2 Be(CN)/Be(AI)-ρ关系
Fig.2 Relationship between Be(CN)/Be(AI)-ρ
(1)两国规范中都通过折减系数来计算杆件整体屈曲承载力.在中国冷弯钢规范(征求意见稿)[4]中,根据截面主轴最大长细比和钢材屈服强度查表,得到折减系数(轴心受压构件稳定系数φ).而美国规范中的折减系数是一个两段计算式,由公式计算获得.如图3所示,采用中国规范计算得到的76个试件的整体屈曲承载力与屈服荷载比值接近于美国规范的整体屈曲强度设计曲线,在整体长细比较小时,中国规范计算的整体承载力要更保守一些.因为依据两国规范公式计算的整体弹性屈曲应力一样,所以整体长细比也一样.
图3 Pne(CN)/Py和Eq.(6)对比
Fig.3 Comparison of the Pne(CN)/Pywith Eq.(6)
(2)对于局部屈曲荷载的计算,两国规范中公式(8)和公式(9)的基本形式是一样的,只是公式系数、指数和分段点不同.中国规范采用手算弹性局部屈曲临界荷载,而美国规范要用数值计算,两者的计算结果相差不大,所以两国规范计算的构件局部长细比基本一致.由图4两国局部荷载设计曲线的对比可见,美国规范要比中国规范保守.以中国规范计算的局部长细比λl为自变量,依据两国规范计算得到的76个试件的局部荷载对比如图5,从图中可以看出,除文献[14]中的无卷边槽形试件外,其余大多数试件依据中国规范计算得到的局部承载力Pnl要大于基于美国规范得到的承载力Pnl.
图5 Pnl(CN/Pnl(AI)-λl关系
Fig.5 Relationship between Pnl(CN/Pnl(AI)-λl
(3)在计算畸变屈曲荷载时,依据中美规范得到的结果差别较大.主要原因在于中国规范考虑了畸变屈曲与整体屈曲的耦合作用.而美国规范则把畸变屈曲当作整体屈曲一样处理,所以用中国规范计算的畸变荷载明显要更小.
中国规范中局部强度设计曲线要比畸变曲线保守不少,如图6所示.所以畸变荷载往往起控制作用,文中依据中国规范计算的试件承载力大多数也是由畸变荷载控制.美国规范把畸变屈曲当作整体屈曲一样对待,往往局部屈曲荷载起控制作用,文献[11]无卷边槽钢因为没有卷边,不少杆件畸变荷载小于局部荷载.因为两国规范计算的局部荷载值相差不大,所以文中多数试件用中国规范计算的承载力要比美国规范偏保守.把由畸变荷载控制的构件试验荷载和我国规范算得的整体荷载比值同我国畸变荷载柱子设计曲线相比较,如图6所示.从图中可以看出我国畸变荷载柱子设计曲线,在长细比很小时,比较保守,随着长细比的增大,保守程度逐渐降低.
图6 Pt/Pne和(Eq.(11))对比
Fig.6 Comparison of the Pt/Pne with(Eq.(11))
(1)有效宽度法计算的关键是板件屈曲系数的计算,虽然中国规范(意见稿)中部分加劲板板件屈曲系数的计算考虑了畸变影响,相对现行冷弯钢规范屈曲系数有所提高,但有些截面部分加劲板件屈曲系数和有效宽度相对美国规范计算值还是明显偏低,中国有效宽度法计算结果相对美国规范还是要偏保守.
(2)直接强度法计算的关键是弹性屈曲临界应力的确定,对于整体弹性屈曲应力,两国规范计算值一样,所以整体长细比也一样.对于局部和畸变弹性屈曲应力,美国规范没有给出具体的理论计算公式,一般采用数值方法计算,本文采用广义梁软件GBTUL进行计算,中国规范给出了具体计算公式.本文计算结果显示:两者计算的局部弹性临界应力相差不大,即局部长细比基本相同,但畸变临界应力相差很大.
(3)依据两国规范直接强度法计算的试件整体和局部屈曲荷载相差不大,但总体美国规范计算值更高一点,畸变荷载的计算相差很大,中国规范考虑了畸变屈曲与整体屈曲的耦合作用,所以计算的畸变荷载明显更低.总体而言,因为中国规范考虑了畸变屈曲与整体屈曲的耦合作用,中国规范直接强度法的计算结果要比美国的更保守一些.
(4)根据本文计算结果可知,中国规范(意见稿)的直接强度法和美国的有效宽度法计算的试件承载力相差不大,与试验数据拟合的较好; 中国规范(意见稿)有效宽度法的计算结果偏保守,所有试件承载力计算值都偏小; 而美国的直接强度法计算的承载力最大,偏危险且波动幅度最大,这主要是由于用广义梁计算的畸变荷载会随试件长度发生明显变化,与理论解不相符,导致构件由畸变荷载控制时,计算不够精确.