(黄河交通学院 交通工程学院,河南 焦作 454950)
(Huanghe Jiaotong University,College of Traffic Engineering, Jiaozuo 454950,China)
Hoek-Brown failure criterion; strain-softening; elasto-plastic analysis; associated flow rule; MATLAB; circular tunnel
DOI: 10.15986/j.1006-7930.2020.02.014
备注
对于传统分析方法无法精准表征围岩的实际变形以及参数演化问题,在H-B准则和应变软化模型结合下选定塑性应变增量作为软化参数,并且假设强度参数随软化参数成线性函数关系.求解塑性区的解答时,将塑性区分成微元圆环,并假设每个圆环的径向应力沿半径向内均匀递减,从而建立每个微元圆环的平衡微分方程、本构方程、几何方程及相邻两微元之间的应力增量和应变增量的关系.最终建立了的圆形隧道在弹塑性交界面以及塑性区内的应力场、应变场和位移场的表达式,并将推导得到的理论表达式通过编程在MATLAB中实现了精准的数值计算,同时验证了程序运行的正确性.在完成上述研究内容以后,下一步将其应用到现场工程隧道中去论证建立理论模型和数值运算程序的实用性,为实现工程现场的稳定性监控和预警做准备.
For the traditional analysis method, the actual deformation of the surrounding rock and the parameter evolution problem cannot be accurately characterized. The plastic strain increment is selected as the softening parameter under the combination of the H-B criterion and the strain softening model, and the strength parameter is assumed to be linearly related to the softening parameter. When solving the solution of the plastic zone, the plasticity is divided into micro-rings, and the radial stress of each ring is uniformly decreased inward along the radius, thus establishing the equilibrium differential equation and constitutive equation of each micro-ring. The geometric equation and the relationship between the stress increment and the strain increment between two adjacent microelements. Finally, the expressions of the stress field, strain field and displacement field of the circular tunnel in the elastoplastic interface and the plastic zone are established, and the theoretical expressions derived are accurately calculated by programming in MATLAB. Verifies the correctness of the program running. After completing the above research content, the next step is to apply it to the field engineering tunnel to demonstrate the practicality of establishing theoretical models and numerical calculation programs, in preparation for the stability monitoring and early warning of the project site.
引言
分析隧道的稳定性通常是通过对隧道进行弹塑性力学分析,求解围岩的应力场、应变场和位移场,进而评价其稳定性[1].对于这类问题的求解,目前应用较广泛的是圆形隧道结构围岩的弹塑性分析.过去对圆形隧道结构围岩的弹塑性分析通常采用Mohr-Coulomb失效准则,因其线性变化,简单方便.随后发现岩石材料的应力 - 应变关系曲线并非是简单的线性关系,而是呈现出一种非线性特性.1980年Hoek和Brown首次提出非线性的失效准则,且迅速在岩石力学领域被广泛地采用[2].二十多年以来,许多研究者不断地发展Hoek-Brown强度准则,最终形成一个完善的体系[3].本文所研究的对象是符合Hoek-Brown强度准则的岩体材料,并对其圆形隧道结构围岩进行弹塑性分析.
Brown等人基于Hoek-Brown强度关联流动法则并通过数值方法计算了弹 - 脆 - 塑性的应力场和径向位移[4].Carranza-Torres和Fairhurst基于Hoek-Brown强度准则对理想弹 - 塑性材料,进行自相似性解答[5].Sharan S.K.计算出了塑性区域的解析解[6].Park和Kim 给出了塑性区位移的理论解答[7].但均是求解Hoek-Brown强度准则参数的情况.当对于没有闭合的解析解时,只能使用数值计算.Lee YK和Pietruszczak S提出一种简便的圆形隧道数值计算方法,分别应用于M-C和H-B应变软化型材料,并通过实例及对比验证该方法的正确性.
对于传统分析方法无法精准表征围岩的实际变形以及参数演化问题,将应用Hoek-Brown强度准则采用应变软化模型来有效分析围岩的稳定性,通过应用相关联流动法则,优化应变软化模型不考虑剪胀角; 通过划分微元推导得到了理想圆形隧道中围岩弹塑性交界面、塑性区内应力场、应变场和位移场的表达式,并将推导得到的关系表达式在MATLAB中实现程序计算.
1 问题的提出
目前岩石力学界对隧道的弹塑性求解主要是应用理想弹 - 塑性模型和弹性 - 脆性 - 塑性模型,而应变软化模型的应用非常有限.如果应用应变软化模型则都是基于Mohr-Coulomb准则的非关联流动法则[8],因为Mohr-Coulomb失效准则形式的塑性势函数计算非常简单,且几乎没有使用相关联流动法则的.岩石材料的应力 - 应变关系曲线并非是简单的线性关系,而是呈现出一种非线性特性,使用Mohr-Coulomb准则的非关联流动法则未能精准表达隧道围岩变形.本文基于Hoek-Brown强度准则应变软化模型,采用关联流动法则来进行研究.
Hoke-Brown强度准则经过不断的修正最终的表达式为
σ1=σ3+σci(mb(σ3)/(σci)+s)a(1)
式中:σ1,σ3分别表示最大最小有效主应力; σci是完整岩石材料的单轴抗压强度; mb、s、a是材料常数,由下式给出.
{mb=miexp((GIS-100)/(28-14D))
s=exp((GIS-100)/(9-3D))
a=1/2+1/6(e-(GIS)/(15)-e-(20)/3)(2)
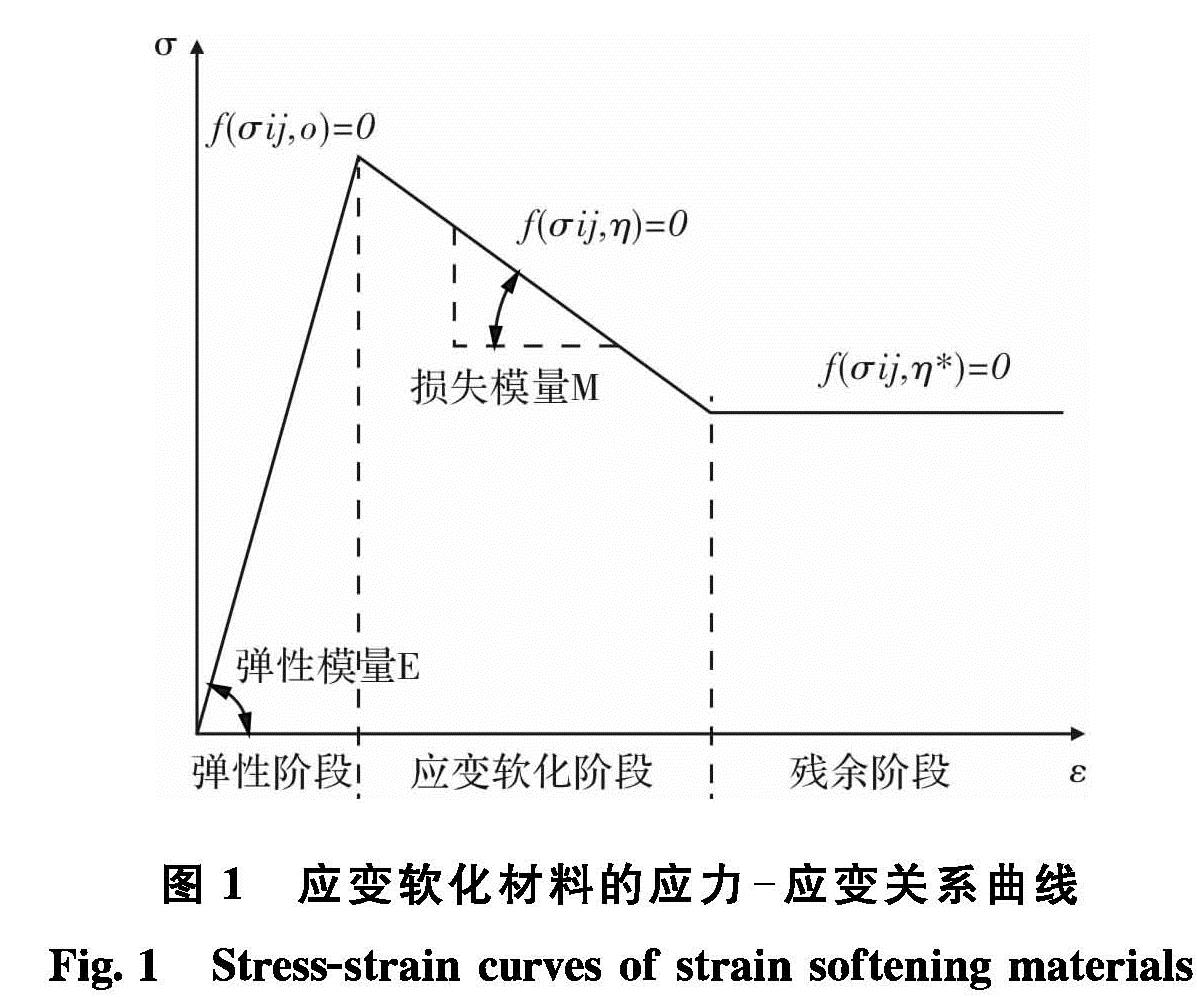
其中:D为扰动参数(D取值为 0.0~1.0,现场无扰动岩体为 0.0,而严重扰动岩体为 1.0)[9].本文中的求解适用于平均质量等级的岩体,即GSI在30~60之间,此时应用应变软化模型求解问题是合理的.选取的应变软化模型为简化的线性模型如图1所示.
应变软化材料的本构方程根据塑性增量理论可以得到.塑性应变增量可以通过塑性势函数得到,定义塑性势函数为g(σr,σθ,η)=0(3)
根据塑性增量理论,可得
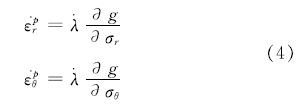
式中:λ.是一个未知的塑性乘数,式(4)是塑性阶段的本构方程,通常称之为流动法则.如果塑性势函数与失效准则一致,就称之为关联流动法则; 否则称为非关联流动法则[10].本文采用关联流动法则,即采用 Hoek-Brown 失效准则形式的塑性势函数.
g(σr,σθ,η)=f(σr,σθ,η)=
σθ-σr-σci(η)[m(η)(σr)/(σci(η))+s(η)]a(η)(5)
同时将软化参数的定义式变换到极坐标形式为
η=εpθ-εpr(6)
选择软化参数作为塑性参数.Hoek-Brown应变软化模型为f(σr,σθ,η)=σθ-σr-H(σr,η)=0
其中
H(σr,η)=
σθ-σr-σci(η)(m(η)(σr)/(σci(η))+s(η))a(η)(7)
公式7在文献[1]中已给出.
2 问题的理论求解
假设地基材料为各向同性材料,弹性模量为E,泊松比为ν,且符合Hoek-Brown失效准则; 此时地基可视为半无限的弹塑性体.设原岩应力为硐室半径为b,长度较长的地下圆形隧道结构; 并且基于这种圆形结构对围岩进行弹塑性分析,求解出应力场、应变场和位移场.这个问题可以看作平面应变问题.围岩的弹塑性分析,归结为弹塑性力学中的平衡微分方程、几何方程和物理方程这三大微分方程的求解.而对于较为复杂的弹塑性力学问题,由于微分方程难于求解,则很难得出精确的理论分析解答.只能是将微分方程近似成代数方程,加以求解,得出满足工程实际的解答.本文基于 Lee YK和Pietruszczak S在文献[1]中提出的差分法,加以改进,并采用相关流动法则,应用MATLAB进行编程求解.
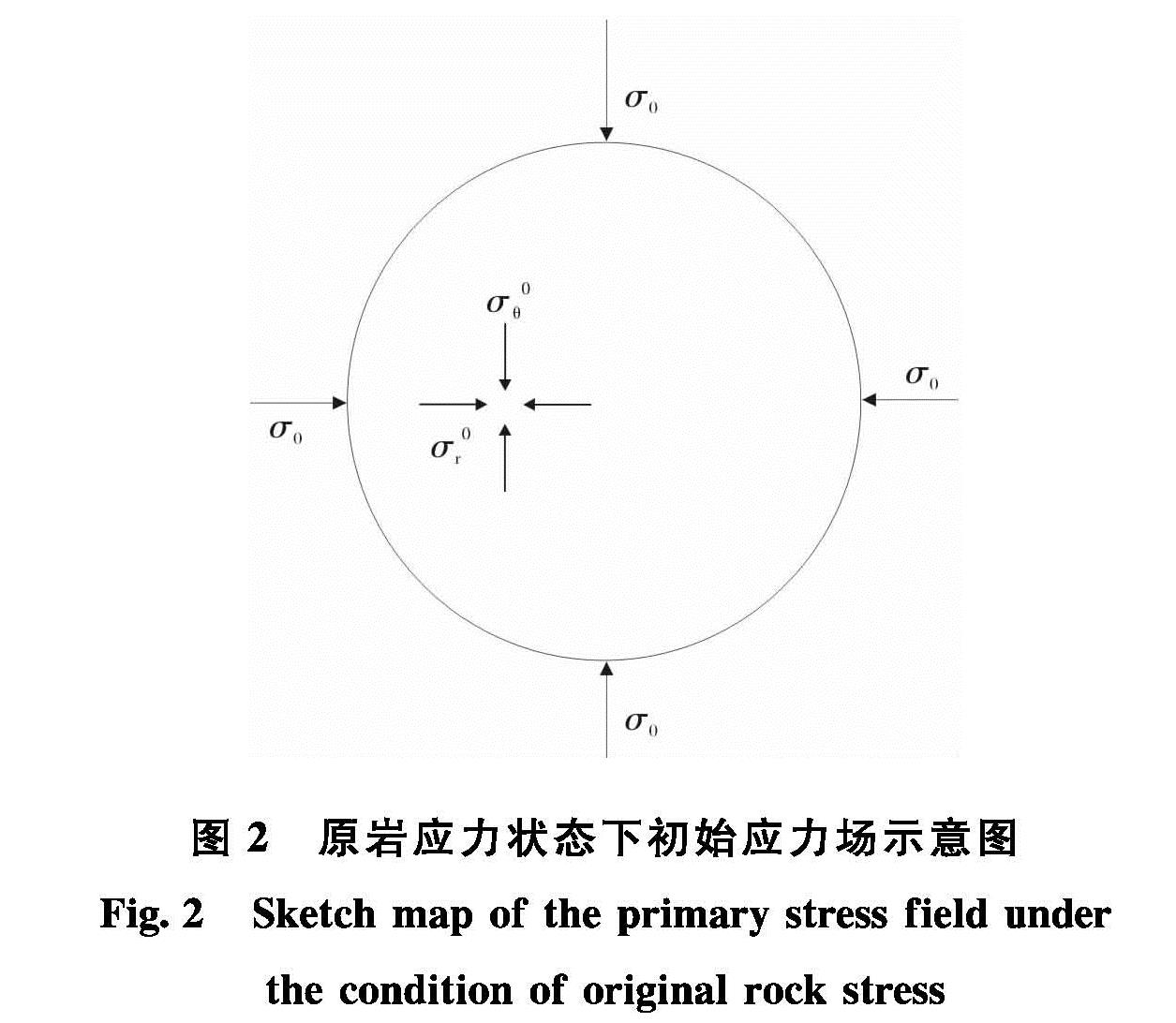
在弹性体中开挖地下硐室之前,围岩体处于原岩应力状态,且原岩应力为σ0,地基材料会产生初始应力σ0r、σ0θ、σ0z,发生初始应变ε0r、ε0θ、ε0z,如图2所示.对围岩进行弹塑性分析之前,首先得求出初始应力值和初始应变值.对于这个问题的求解依然可以归结为平面应变问题(ε0z=0),由广义胡克定律(Hooke's law)可得
{ε0r=(1+ν)/E[(1-ν)σ0r-νσ0θ]图2 原岩应力状态下初始应力场示意图
Fig.2 Sketch map of the primary stress field under the condition of original rock stressε0θ=(1+ν)/E[-νσ0r+(1-ν)σ0θ]
ε0z=0(9)
由弹性力学基础知识可知,围岩体处于原岩应力状态时,岩体内径向应力和环向应力都等于原岩应力σ0,即
σ0r=σ0θ=σ0(10)
将式(10)代入式(9)可得
{ε0r=(1+ν)/E(1-2ν)σ0
ε0θ=(1+ν)/E(1-2ν)σ0
ε0z=0(11)
式(10)及式(11)就是初始应力和初始应变的解答,即天然状态下(原岩应力状态)岩体的应力场和应变场.开挖地下硐室之后,应力状态会改变,应变也会随之改变.我们关注的便是开挖引起的应变的改变量和位移的改变量,以此来衡量地下硐室的稳定性.接下来,我们便列方程求出开挖之后的总应力场和应变场,再减去初始应力场和应变场就可以得到改变量了.
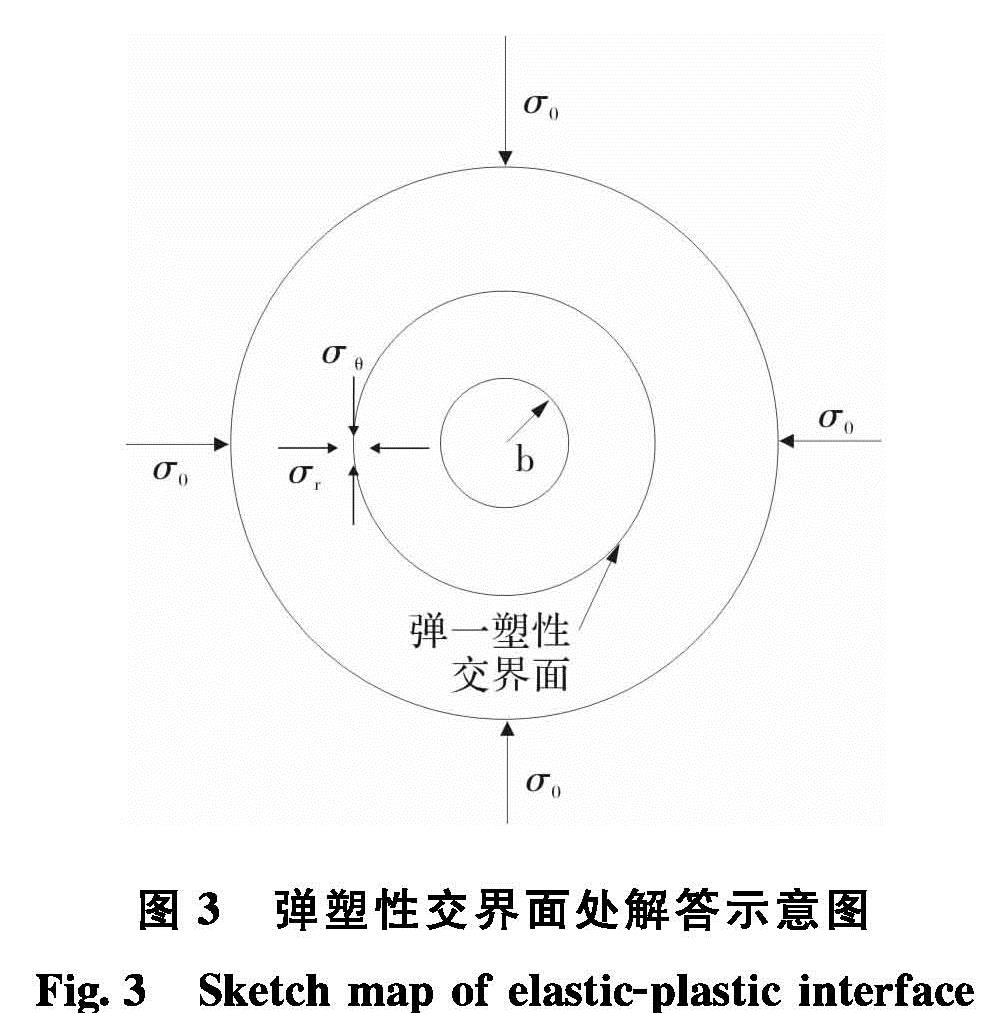
(1)在弹塑性交界面处,即可列三大方程
平衡微分方程:
(dσr)/(dρ)+(σr-σθ)/ρ=0(12)
几何方程:
εtotalr=(dutotalr)/(dρ),
εtotalθ=(utotalr)/ρ,
εtotalz=0(13)
物理方程:{εtotalr=1/E[σr-ν(σθ+σz)]
εtotalθ=1/E[σθ-ν(σr+σz)]
εtotalz=1/E[σz-ν(σr+σθ)](14)
边界条件:
{当ρ=Rp时,则有σr=σR
当ρ=∞时,则有σr=σ0
联立以上方程解得应力场和应变场.
{σr=σ0-(σ0-σR)((Rp)/ρ)2
σθ=σ0+(σ0-σR)((Rp)/ρ)2
σz=ν(σr+σθ)=2νσ0(15a)
{εtotalr=(1+ν)/E[(1-2ν)σ0-(σ0-σR)((Rp)/ρ)2]
εtotalθ=(1+ν)/E[(1-2ν)σ0+(σ0-σR)((Rp)/ρ)2]
εtotalz=0(15b)
需要指出的是,这里的应变εtotalr,εtotalθ,εtotalz和位移utotalr都是包括了原岩应力状态下的初始应变和初始位移的.我们所关注的并不是开挖后的总应变和总位移,而是由于开挖所引起的应变的变化量和位移的变化量.所以,最终的结果(应变,位移)都需要扣除原岩应力状态下的初始应变值和初始位移值.可以事先就扣除初始应变,即将此时的解答中的应变由此而求出弹塑性交界面处的应变值,此值将作为下文中的塑性区域应变场和位移场的初始值来循环计算,进而此值将被应用于所有应变.再将这些应变带入几何方程中求出位移.这样一来,最终的结果便是由于开挖所引起的应变的变化量和位移的变化量.则有
{εr=εtotalr-ε0r=(1+ν)/E(σR-σ0)()2
εθ=εtotalθ-ε0θ=(1+ν)/E(σ0-σR)()2
εz=εtotalz-ε0z=0(16)
式中εr,εθ,εz均是指由于开挖引起的应变的增量,而不是包含初始应变的总应变.下文中所提及的均是指由于开挖引起的应变的变化量,而不是由平常弹性力学里的三大方程直接求解出来的总值.
在弹塑性交界面上,当 ρ=σR时,代入上式可得:
{σr=σR
σθ=2σ0-σR
σz=2νσ0(17a)
{εr=(1+ν)/E(σR-σ0)
εθ=(1+ν)/E(σ0-σR)
εz=0(17b)
这个应力,应变的解答就是弹塑性交界面的应力应变解答,并将作为后续循环的初始值.下文塑性区的求解会将其视为已知的初始条件.这里还需要赘述的是,式(16)的结果是采用广义胡克定律在弹塑性边界上求解的.而这个解答也正是岩石力学领域里的前辈们,如Lee YK和Pietruszczak S[1],E.Alonso 等人[11]所引用的.此解答最早在 Brown 等人在 1983 年的文章[12]中提出来,此后相关研究人员都引用该文章,采用此解答作为弹—塑性交界面上的应力应变的解答.
在弹塑性交界面上,显然应力状态 σθ和σr满足失效准则:f(σr,σθ,η)=σθ-σr-H(σr,η)=0,将σθ和σr带入失效方程,可得:
2(σ0-σr)-σci(η)(m(η)(σR)/(σci(η))+s(η))a(η)=0(18)
解此方程可得到 σR的值.但是(Carranza-Torres 和 Fairhurst, 1999[5]; Park 和 Kim,2006[7])需要指出的是,此方程的理论解答只能求解 a(η)=0.5时的失效方程.即
2(σ0-σr)-σci(η)(m(η)(σR)/(σci(η))+s(η))0.5=0(19)
对于a(η)更为一般的情况,只能应用数值逼近求解,本文应用MATLAB对(18)进行数值求解,从而保证计算曲线更加光滑不间断,也更加符合工程实际.
(2)临界支护压力pic
显然,只有当硐室的支护力pi<pic 时,硐室周围的岩石材料才会发生屈服,继而会在硐室附近形成塑性区域.否则,当硐室的支护力 pi≥pic时,硐室周围的岩石材料不会发生屈服破坏,也不会形成塑性区域.当硐室的支护力 pi=pic时,硐室边界处刚好发生屈服; 则此边界为弹塑性交界面. 此时有:
{σr=pic
σθ=2σ0-pic
σz=2νσ0(20)
在此边界上,应力状态满足失效准则式
f(σr,σθ,η)=σθ-σr-H(σr,η)=0
由方程式得:
pic=σR(21)
此项数值可由MATLAB进行求解
(3)塑性区的解答
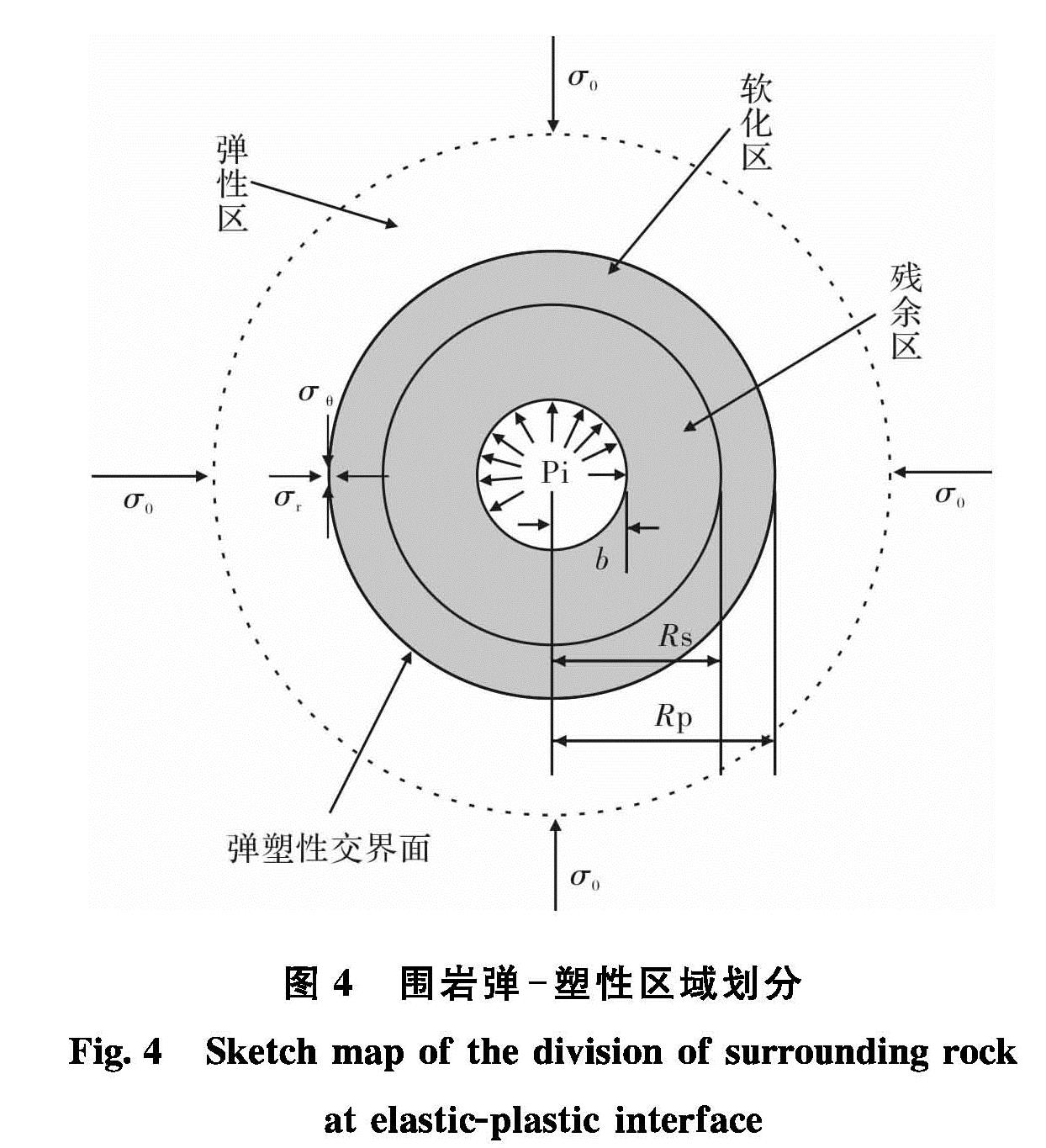
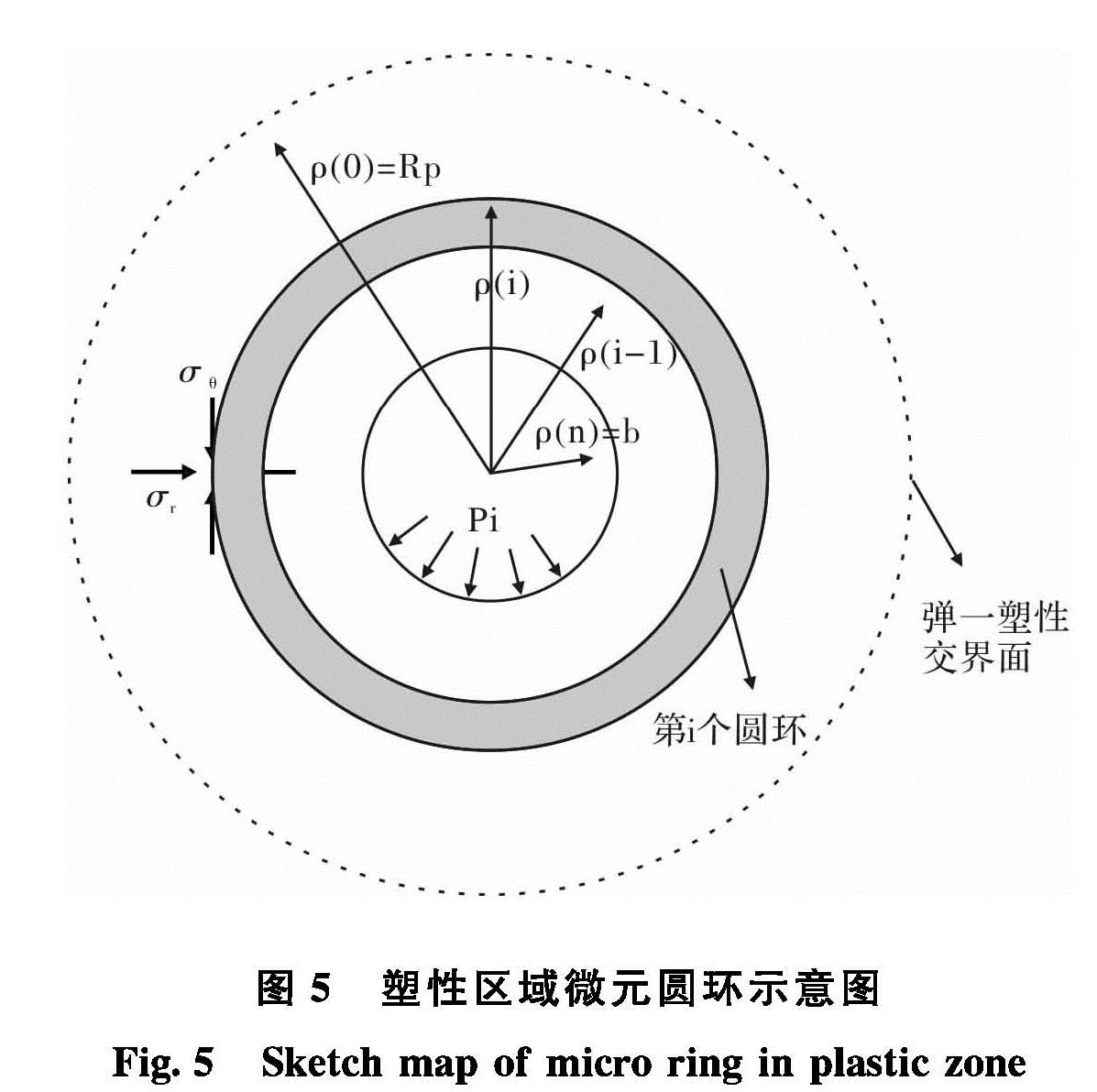
在硐室表面沿径向加上支护力,且硐室的支护力pi<pic时,会在硐室周围形成塑性区域. 如果采用应变软化模型,塑性区将分为软化区和残余区,塑性区半径为Rp,残余半径为Rs如图4所示,此时塑性区得不闭合解[11].
我们将塑性区分为 n 个同心微元圆环,并假设径向应力σr沿每个圆环均匀递减,从弹塑性交界面ρ0=Rp处,σr(0)=σR; 递减到隧道壁ρn=b 处,σr(n)=pi.如图5所示.由此可以得出径向应力增量Δσr.
Δσr=(pi-σR)/n=σr(i)-σr(i-1)(22)
显然,当 n 足够大时,解答会更加精确.
值得注意的是,每个圆环的厚度并不是相等的,而是满足平衡方程和上述增量方程式而计算求得的[1],也就是说,径向应力σr并不是沿半径长度方向均匀递减的.Brown等人1983年[4]在文章中提出的方法,对塑性区的弹性应变做了简单的假设.本文基于Lee YK和Pietruszczak S[1]提出的差分法,便克服了这个缺点,使得计算结果更加符合工程实际.塑形区的解答也是求解三大微分方程. 平衡微分方程,对于二维平面问题,一般形式的平衡微分方程为式(23)(dσr)/(dρ)+(σr-σθ)/ρ=0(23)
将上式变换应用到第 i 圈,即列出第 i 圈的平衡微分方程.根据差分法的一般思路,将微分方程式用微元的代数方程替换,从而求出近似的数值解答:
dσr=σr(i)-σr(i-1)
dρ=ρ(i)-ρ(i-1)(24)
在塑性区,岩石材料已然屈服,则其应力状态始终满足失效准则方程,即
f(σr,σθ,η)=σθ-σr-H(σr,η)=0
则第i圈的应力状态σr(i),σθ(i)满足
σr(i)-σθ(i)=-H(σr(i)-,η(i-1))(25)
式中:σr(i)-为第i圈的平均径向应力,其表达式为σr(i)-=1/2(σr(i)+σr(i-1)),半径ρ用圆环的平均半径计.由以上各式可得
(σr(i)-σr(i-1))/(ρ(i)-ρ(i-1))-(H(σr(i)-,η(i-1)))/(1/2(ρ(i)-ρ(i-1)))=0(26)
对上式进行变形可以得到可求得第 i 圈的半径与第i-1圈的半径之间的关系.
ρ(i)=(2H(σr(i)-,η(i-1))+Δσr)/(2H(σr(i)-,η(i-1))-Δσr)·ρ(i-1)(27)
当i=1时,则有ρ(0)=Rp
当i=n时,则有ρ(n)=b
经过 n 次迭代可求得
ρn=∏ni=1(2H(σr(i)-,η(i-1))+Δσr)/(2H(σr(i)-,η(i-1))-Δσr)·ρ(0)(28a)
即
ρn=∏i=1n(2H(σr(i)-,η(i-1))+Δσr)/(2H(σr(i)-,η(i-1))-Δσr)·Rp(28b)
因此,可求得塑性区半径 Rp的表达式.
Rp=b/(∏i=1n(2H(σr(i)-,η(i-1))+Δσr)/(2H(σr(i)-,η(i-1))-Δσr))(29)
应变软化材料的本构方程是根据塑性增量理论[13]得到的.此时的本构方程习惯称为流动法则,而我们采用的是相关联流动法则,根据流动法则以及软化参数
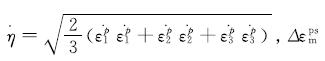
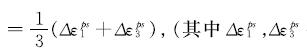
代表主塑性剪切应变增量)可得
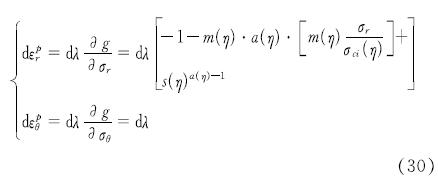
联立消去dλ,则有
dεpr=-k(σr,η)dεpθ(31)
k(σr,η)=1+m(η)·a(η)·
[m(η)(σr)/(σci(η))+s(η)a(η)-1]
其中:由流动法则可得,将式(31)写成微元代数差值表达式,则有第i圈的塑性应变增量之间的关系为:
Δεpr(i)=-k(i-1)·Δεpθ(i)(32)
Brown等人1983年[4]在文章中指出几何相容方程(dεθ)/(dρ)+(εθ-εr)/ρ=0,将其进行变形,将应变分为弹性应变和塑性应变,εθ=εpθ+εeθ,εr=εpr+εer,得到:
(dεpθ)/(dρ)+(εpθ-εpr)/ρ=-(dεeθ)/(dρ)-(εeθ-εer)/ρ(33)
式(33)称为塑性区的几何相容方程.
对于平面应变问题,εz=0,我们把εz=0代入物理方程可得
{εer=(1+ν)/E[(1-ν)σr-νσθ]
εeθ=(1+ν)/E[(1-ν)σθ-νσr](34)
则有
εeθ-εer=(1+ν)/E(σθ-σr)(35)
在弹塑性交界面上,σθ和σr满足失效准则,将失效准则代入(35)有
εeθ-εer=(1+ν)/EH(σr,η)
dεpθ=εpθ(i)-εpθ(i-1)(36)
将(36)代入(33)可得到第i圈的几何相容方程为:
(εpθ(i)-εpθ(i-1))/(ρ(i)-ρ(i-1))+(εpθ(i)-εpr(i))/(ρ(i)-)=
-(εeθ(i)-εeθ(i-1))/(ρ(i)-ρ(i-1))-(εeθ(i)-εer(i))/(ρ(i)-)(37)
根据差分法,第 i圈的应变等于第(i-1)圈的应变加上一个增量,可得下式.
{εpθ(i)=εpθ(i-1)+Δεpθ(i)
εpr(i)=εpr(i-1)+Δεpr(i)
{εeθ(i)=εeθ(i-1)+Δεeθ(i)
εer(i)=εer(i-1)+Δεer(i)(38)
联立(37),(38)可解出塑性应变增量Δεpθ(i)、Δεpr(i),即
{Δεpθ(i)=(-(Δεeθ(i))/(Δρ(i))-(1+ν)/E(H(σr(i)-,η(i-1)))/(ρ(i)-)-1/(ρ(i)-)(εpθ(i-1)-εpr(i-1)))/(1/(Δρ(i))+(1+k(i-1))/(ρ(i)-))
Δεpr(i)=-k(i-1)·(-(Δεeθ(i))/(Δρ(i))-(1+ν)/E(H(σr(i)-,η(i-1)))/(ρ(i)-)-1/(ρ(i)-)(εpθ(i-1)-εpr(i-1)))/(1/(Δρ(i))+(1+k(i-1))/(ρ(i)-))(39)
第 i 圈的总应变 ε(i)可由三部分组成:第(i-1)圈的总应变、弹性应变增量和塑性应变增量.
由此可得应变分量,即
{εr(i)=εr(i)+Δεer(i)+Δεpr(i)
εθ(i)=εθ(i)+Δεeθ(i)+Δεpθ(i)(40)
以及应力分量的表达式,即
{σr(i)=σr(i-1)+Δσr
σθ(i)=σθ(i-1)+H(σr(i)-,η(i-1))(41)
将弹塑性交界面处的应力应变分量作为初始值,经过n次迭代循环,即可求解出塑性区域里的应力场和应变场.至于位移, 我们所关心的是径向位移,它在某种程度上可以评价支护系统的支护效果.而环向位移给不出具体的工程实践价值,不予求解了.而径向位移u,由几何方程式求得u=εθ·ρ[14,15].
3 实例验证
本文采用Lee YK和Pietruszczak S在文献[1]中给出的数据,利用MATLAB 进行编程求解,并讨论相关问题.
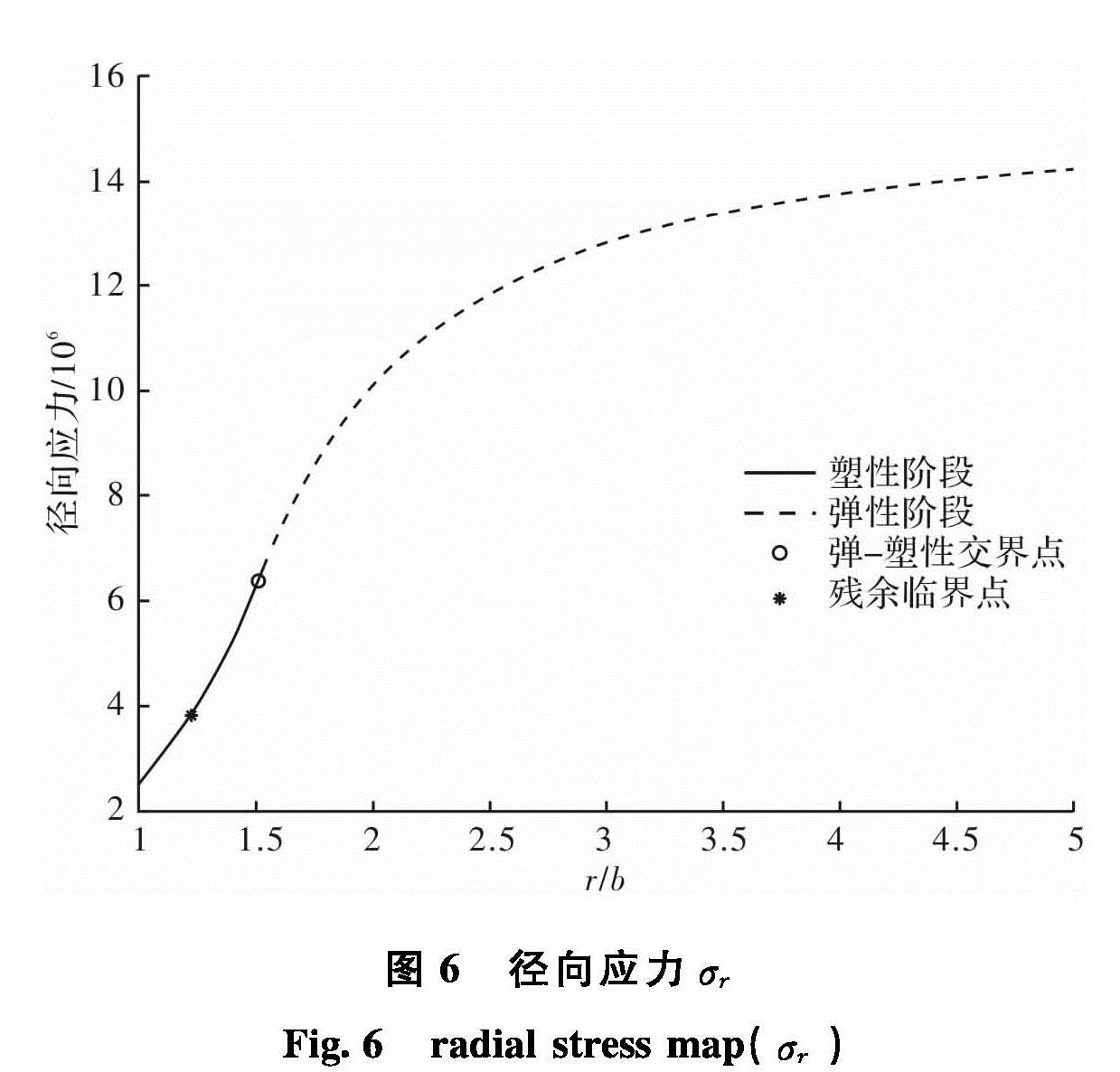
隧道半径b=2,弹性模量E=5 700 MPa,泊松比ν=0.3,原岩应力σ0=15 MPa,硐室周围所加支护力pi=2.5 MPa,Hoek-Brown强度准则峰值参数[σcp=30 MPa,mp=1.7,sp=3.9e-3,ap=0.55],残余参数[σcr=25 MPa,mr=0.85,sr=1.9e-3ar=0.6,软化参数临界值η*=12e-3].计算结果如下图6所示:径向应力σr
图6所示的径向应力σr图曲线分为三个阶段:弹性阶段,软化阶段,残余阶段.而且曲线相当的平滑,各个阶段的过渡还是较为吻合的.我们还可以由图中的信息,做如下几点讨论:从弹塑性交界面开始,在软化阶段中,σr是接近于直线变化的一条平缓曲线.从r/b=1(硐室侧壁)开始,一直到残余临界点处,即残余阶段,σr几乎成一条直线变化.这是由于我们的理论假设所导致的.图7是各个变形阶段.图6 径向应力σr
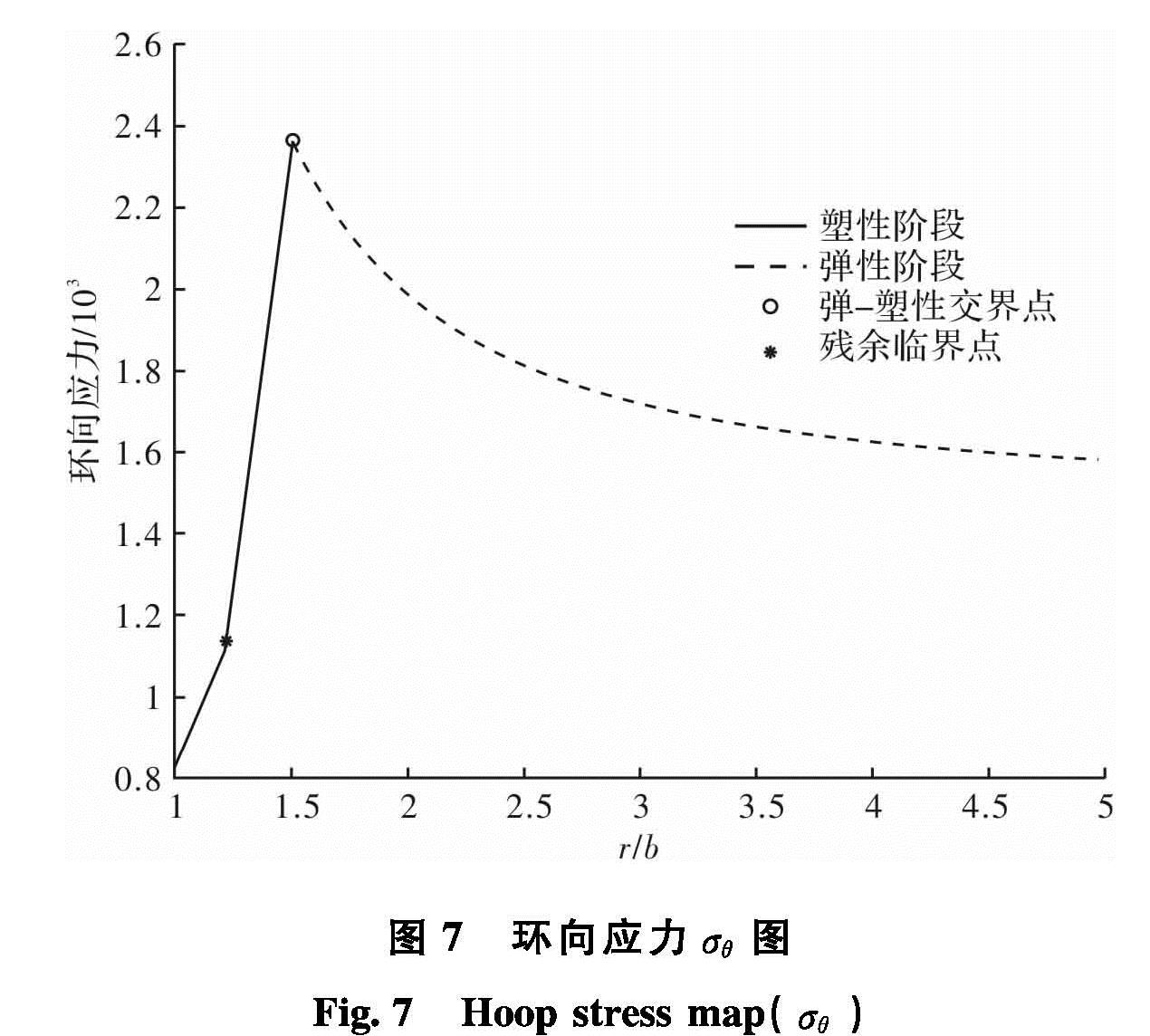
Fig.6 radial stress map(σr)图7所示的环向应力σθ图曲线也可以分为这三个阶段(弹性阶段,软化阶段,残余阶段).σθ在弹塑性交界面处达到最大值,而σθ在塑性阶段呈分段的线性变化:软化阶段变化斜率较大,而残余阶段变化较小.
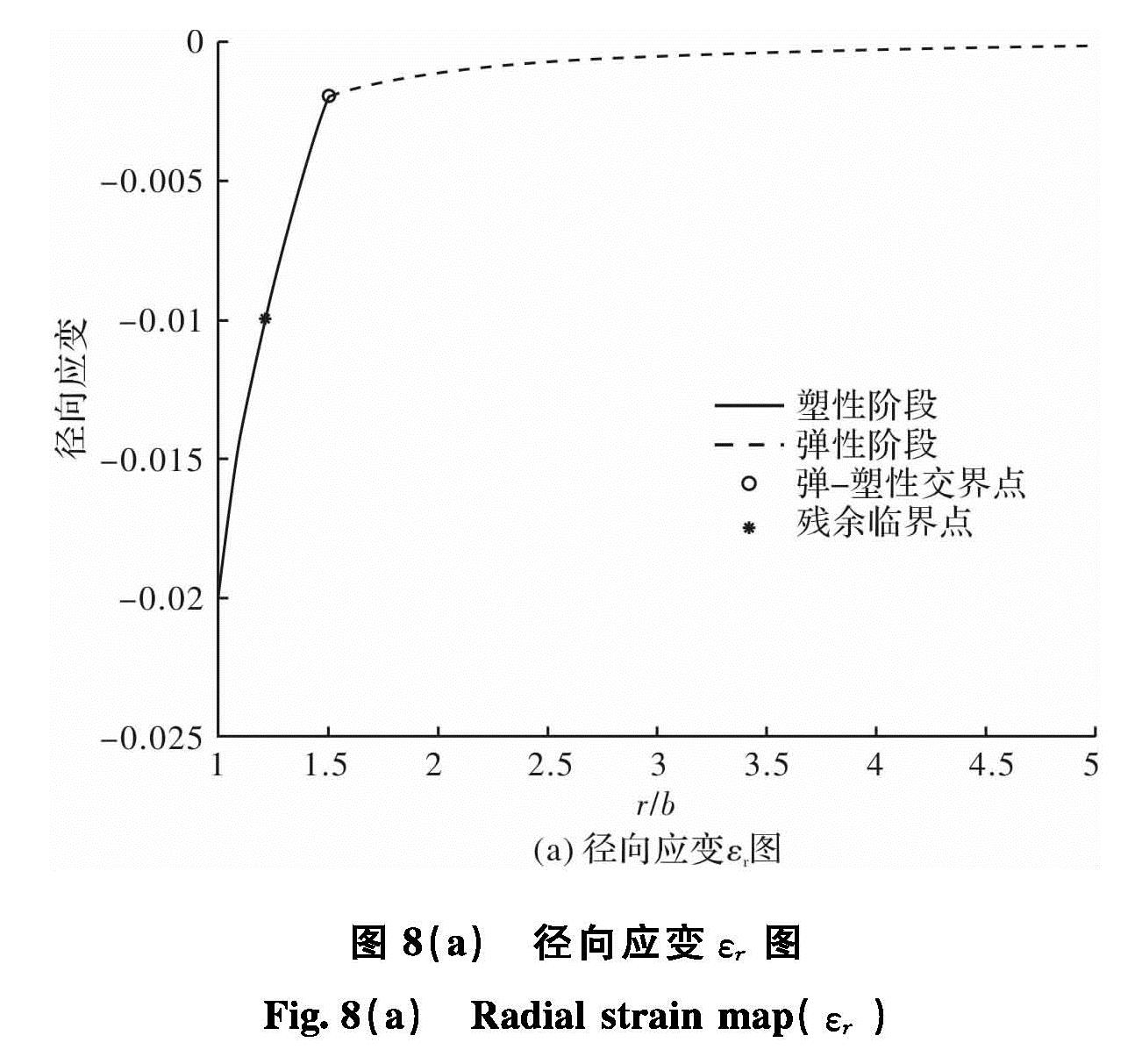
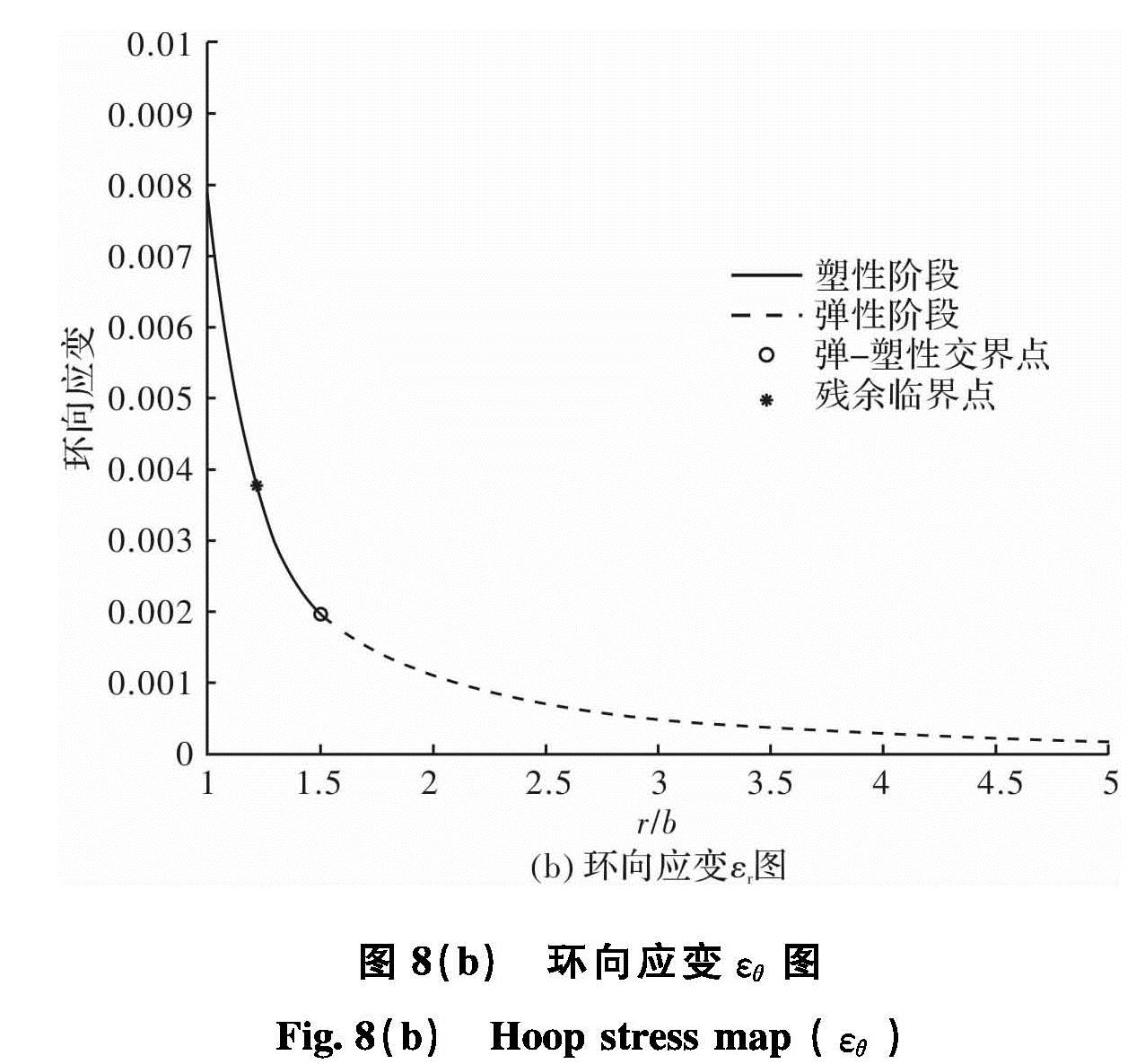
图8(a)和图8(b)所示的是应变εr,εθ解答图.这里的应力应变是开挖前后应变和位移的变化量.图中结果显示εr,εθ都逐渐变小,最后都趋于零.这与岩石力学的理论分析是一致的.从图中还可以看出,弹性区的应变变化量很小,这表明开挖对弹性区域的影响较小.也就是说,开挖前后弹性区的应变改变量很小.图8(a)所示的径向应变图在弹—塑性交界面处产生突变点,使得弹—塑性两阶段过渡不够平滑,这是由于所选取的应变软化模型是简化的线性模型的缘故.而图8(b)所示的环向应变解答图非常平滑顺畅,解答的趋势也很符合实际; 即使在弹—塑性交界面处依然过渡平顺.这也充分说明本文数值计算的正确性.图7 环向应力σθ图
Fig.7 Hoop stress map(σθ)图8 (a)径向应变εr图
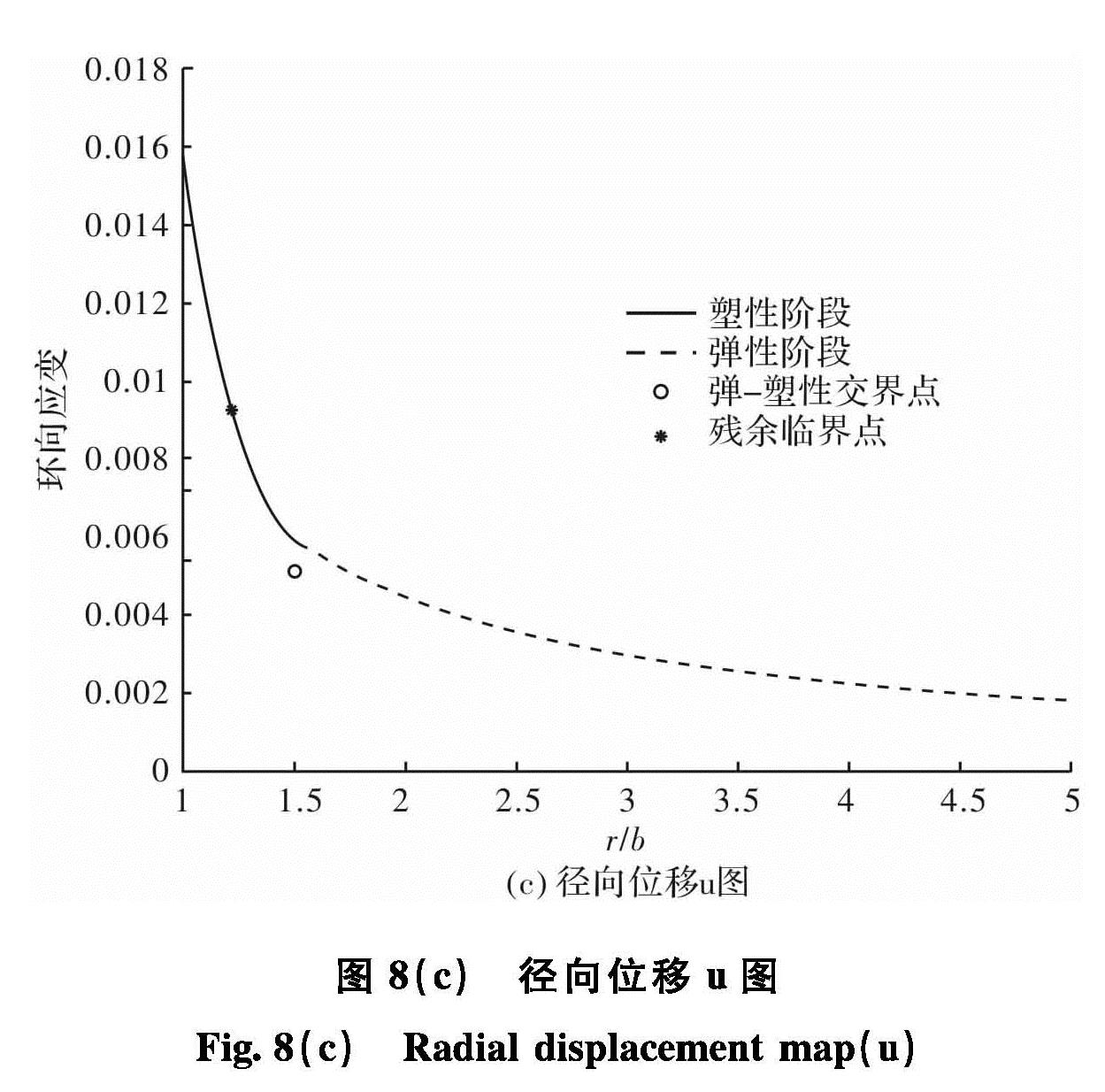
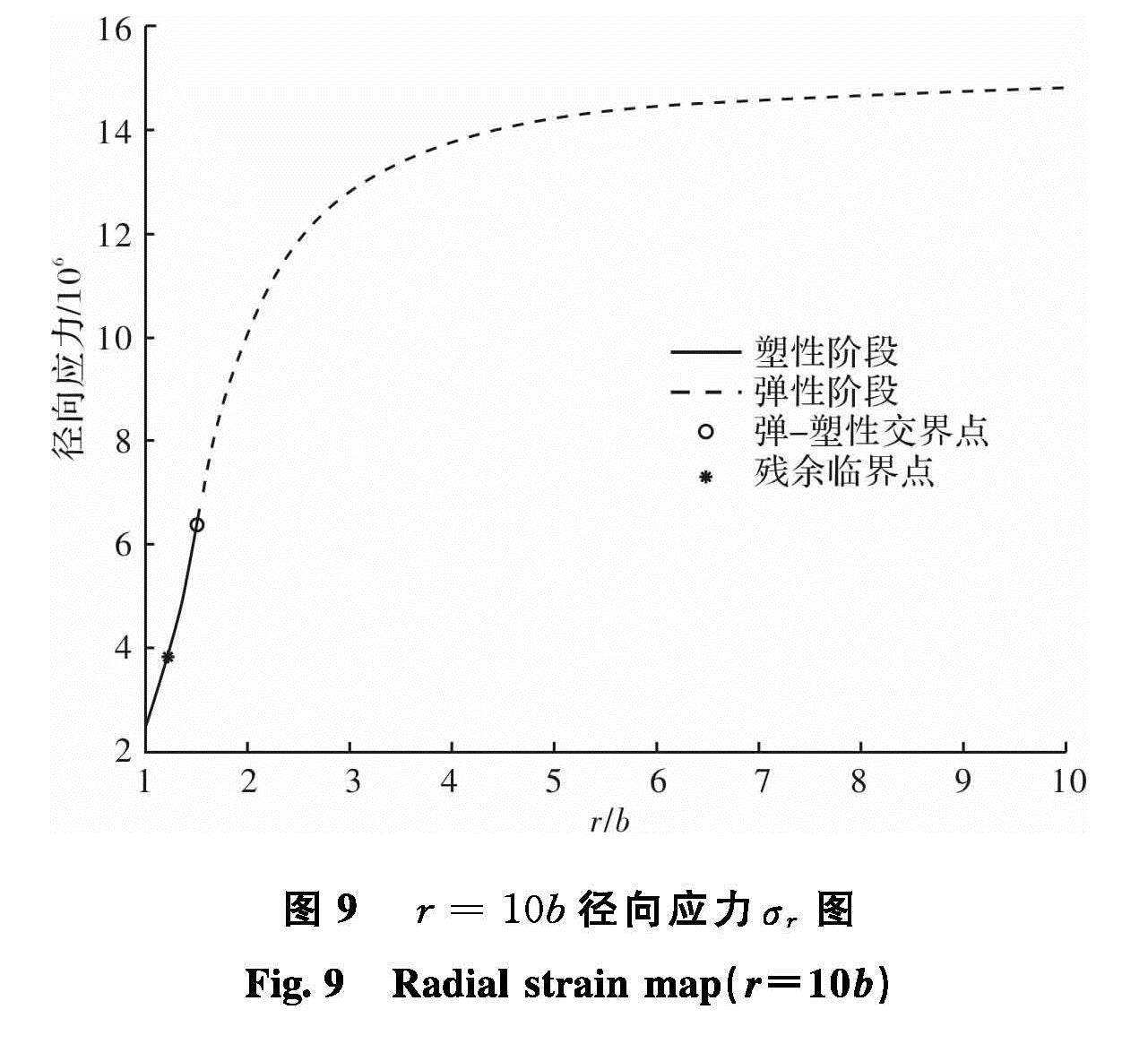
Fig.8 (a)Radial strain map(εr)图8(c)所示的是径向位移 u 图,径向位移可以在某种程度上说明支护系统的有效性,而环向位移却给不出具体的工程实际意义.由图可以看出径向位移u图曲线还是比较平滑,曲线形状几乎与环向应变εθ图相同,径向位移u由u=εθ·ρ求得,所以两曲线形状几乎一样.如图9所示在r=10b处的径向应力值基本已经达到15 MPa,这也符合岩石力学的理论解答.在r=7b-10b 基本可以达到原岩应力的 97%,此时可以认为已经是原岩应力区了,即未受到扰动的岩体区域.图8 (b)环向应变εθ图
Fig.8 (b)Hoop stress map(εθ)图8 (c)径向位移u图
Fig.8 (c)Radial displacement map(u)本文采用Lee YK 和 Pietruszczak S 在文献[1]中给出的数据,利用 MATLAB进行编程求解,并讨论相关问题.应力场、应变场和位移场的求解结果图还是比较平滑,各个阶段的过渡还是相当的顺畅.总体而言,是吻合理论分析和工程实践的.图9 r=10b径向应力σr图
Fig.9 Radial strain map(r=10b)4 结论
本论文基于Hoek-Brown强度准则应变软化模型对圆形隧道进行稳定性的分析得出以下结论:
(1)提出一种简单的数值计算方法来对围岩进行弹塑性分析.其中的核心工作是利用MATLAB进行编程求解围岩的应力场、应变场、位移场的数值解答,分析影响解答的因素,以及分析影响塑性区半径的因素.
(2)基于Lee YK和Pietruszczak S[1] 提出的差分法,进行两点改进.改进之一是对于弹塑性交界面处的径向应力的情况,使用数值计算得出.这样使得求解能代表更为一般的情况,并且也使得与后续利用广义形式的Hoek-Brown 失效准则的解答更为一致; 另一个重大改进是——采用相关流动法则,即使用广义 Hoek-Brown 失效准则形式的塑性势函数,建立相关联的本构方程.这样使得本文解答不依赖于剪胀角这个参数,也减少了影响解答的因素.
本论文也存在着一些缺陷与有待改进之处:对于径向应变的解答在弹—塑性交界面处始终不能过渡平滑,不能令人满意.本文采用目前国内外研究学者广为采用的软化特性模型,即失效准则参数随着软化参数的演化规律为分段线性函数.这种线性函数始终显得对问题过于简化,而使得计算结果无法达到满意的期望.今后可以在这方面做一些研究工作:采取大量的实验测量这些参数的变化规律,然后对结果进行多项式的拟合,以期找到更为符合客观事实的演化规律.这样会使得计算结果更为平滑,更为符合工程实践.同时可以使Hoek-Brown强度准则应用于多个工程领域.
- [1] LEE YK, PIETRUSZCZCAK S, et al. A new numerical procedure for elasto-plastic analysis of a circular opening excavated in a strain-softening rock mass[J]. Journal of Tunnel and Underground Space Technolgy, 2008, 23(5): 588.
- [2] HOEK E, CARRANZA-TRRES C T, CORCUM B. Hoek-Brown failure criterion[C]// Proceedings of the North American Rock Mechanics Society. Toronto: Mining Innovation and Technology, 2002: 267.
- [3] 朱合华,张琦,章连洋. Hoek-Brown 强度准则研究进展与应用综述[J].岩石力学与工程学报2013, 32(10): 1946.
- [4] BROWN E T, BRAY J W, LADANYI B, et al. Ground response curves for rock tunnels[J]. Journal of Geotechnical Engineering, 1983, 109(1): 15.
- [5] CARRANZA-TORRES C, FAIRHURST C, The elasto-plastic response of underground excavations in rock masses that satisfy the Hoek-Brown failure criterion[J]. Journal of Rock Mechanics and Mining Sciences. 1999, 36(6): 777.
- [6] SHARAN S K, Elasto-brittle-plastic analysis of circular opening in Hoek-Brown media[J]. Journal of Rock Mechanicsand Mining Sciences, 2003, 40(6): 817.
- [7] PARK K H, KIM Y J, Analytical solution for a circular opening in an elasto-brittle-plastic rock[J]. Journal of Rock Mechanics and Mining Sciences, 2006, 43(4): 616.
- [8] 薛海斌, 党发宁, 尹小涛, 等. 应变软化边坡稳定性分析[J].岩土工程学报, 2016, 38(3): 571.
- [9] 彭俊, 荣冠, 周创兵, 等. 一种基于GSI弱化的应变软化模型[J]. 岩土工程学报, 2014, 36(3): 500.
- [10]SORENSEN E S, CLAUSEN J, DAMKILDE L.Finite element implementation of the H-B material model with general strain softening behavior[J], International Journal of Rock Mechanics and Mininng Sciences,2015.
- [11]刘冬桥,王焯,张晓云.岩石应变软化特性和损伤本构模型研究[J],岩土力学,2017,38(10):2901.
- [12]李守龙,李宗利,黄高峰.Hoek-Brown强度准则在隧道岩体稳定分析中的应用研究[J],长江科学院院报,2014,31(5):43.
- [13]曹日红,曹平,张科,等.考虑应变软化的巷道交叉段稳定性分析[J].岩土力学,2013,34(6): 1760.
- [14]陈梁,茅献彪,李明,等.基于 Drucker-Prager 准则的深部巷道破裂围岩弹塑性分析[J].煤炭学报,2017,42(2):484-491.
- [15]温森,杨圣奇.基于 Hoek-Brown 准则的隧洞围岩变形研究[J].岩土力学,2011,32(1):63-69.