基金项目:国家自然科学基金资助项目(51508347,51768042); 河北省自然科学基金资助项目(E2019210215,E2015210038); 河北省高等学校科学技术研究基金资助项目(ZD2019124)
第一作者:张航源(1995-),男,硕士,研究方向为桥梁抗震.E-mail:435051747@qq.com 通信作者:王军文(1971-),男,教授,博士生导师,主要从事桥梁抗震方向的研究.E-mail:wjunwen2901@163.com
(1.石家庄铁道大学 土木工程学院,河北 石家庄 050043; 2.北京铁路局丰台工务段,北京 100071 3.道路与铁道工程安全保障省部共建教育部重点实验室(石家庄铁道大学),河北 石家庄 050043)
(1. School of Civil Engineering, Shijiazhuang Tiedao University, Shijiazhuang 050043, China; 2.Fengtai Working Section of Beijing Railway Bureau, Beijing 100071, China; 3.Key Labratory of Roads and Railway Engineering Safety Control(Shijiazhuang Tiedao University), Ministry of Education, Shijiazhuany 050043, China)
continuous skew bridge; seismic capability; pushover analysis; IDA analysis; redundancy; robustness
DOI: 10.15986-j.1006-7930.2020.04.011
以某高速公路三跨连续斜交桥为研究对象,利用OpenSees软件建立不同斜度的全桥有限元计算模型,采用Pushover方法得到结构的能力谱曲线,基于抗震冗余度理论分析了斜度对三跨连续斜交桥冗余度需求比r的影响; 运用增量动力分析(IDA)法求出结构的地震易损性曲线,基于抗震鲁棒性理论研究了斜度对抗倒塌储备系数RCM的影响.结果表明:冗余度需求比r与抗倒塌储备系数RCM均随斜度的增加而减小,且两者间存在较好的线性相关关系,说明可以使用抗震冗余度理论对连续斜交桥的抗震鲁棒性和抗震性能进行评价.
Taking a three-span continuous skewed girder bridge on a highway as the research object, OpenSees software was used to establish the full-bridge finite element model with different skew degree. The structural capacity spectrum curve was obtained by pushover method, and based on seismic redundancy theory, the effect of skew degree on the redundancy demand ratio r for a three-span continuous skewed girder bridge was analyzed. The structural seismic fragility curve was determined by a incremental dynamic analysis(IDA)method, and the influence of skew degree on the anti-collapse reserve coefficient RCM was studied on basis of seismic robustness theory. Results show that the redundancy demand ratio r and the anti-collapse reserve coefficient RCM decrease with the increase of skew degree, and there is a good linear correlation between the two indexes, which shows that the seismic robustness and seismic performance of the continuous skewed girder bridge could be evaluated by the redundancy theory.
斜交桥自身独特的外形,导致其振动特性与地震响应非常复杂.为此,许多学者对斜交桥的抗震性能进行了大量基础研究[1-4],但目前研究多集中在对斜交桥抗震能力的定性分析,对斜交桥抗震能力的精细化定量分析比较欠缺.
在1967年美国垮塌的Silver桥事故中调查发现,结构中没有多余的传力路径,会降低桥梁整体的抗倒塌能力[5].因此,如何适当的在结构中增加传力路径,改善结构受力状态,提高结构冗余度,引起了学者们的关注.1996年AASHTO规范中首次明确给出了冗余度设计原则.但是目前在建筑结构领域中冗余度理论研究较为广泛[6-8],针对于桥梁领域的冗余度的研究比较缺乏[5].据此,如何在桥梁领域中运用结构冗余度理论量化分析桥梁结构的抗震性能,需要深入的研究.
鲁棒性理论的提出为更好的评价桥梁抗震性能提供了一种新的思路,桥梁抗震鲁棒性的适当提高不仅可以在一定程度上减小地震作用下桥梁结构的损伤概率,还能在震后的救援和重建工作中提供重要保障[9].但鲁棒性的理论性较强,评价指标[8]计算复杂,不利于实际工程的应用.由于结构冗余度理论和鲁棒性两者概念上的共性,本文拟将结合两者各自优点,将冗余度指标体现的斜交桥抗震性能与斜交桥抗震鲁棒性进行对比,探究采用相对简便的冗余度理论对斜交桥的抗震鲁棒性进行评价.
冗余度体现了结构承受意外损害的能力,即在整体结构中某些构件失效时,结构整体依然有支撑荷载的能力.SEAOC把结构具有多道抗力路径的特性表述为冗余度,NCHRP把冗余度分为局部冗余度,结构整体冗余度和传力路径冗余度三类.现阶段,基于承载力、可靠度和灵敏度分析的三类冗余度指标得到专家学者的广泛认同.
为了直观的体现和评价结构的抗震性能,能力谱法将结构的能力谱曲线和地震动需求谱曲线绘制在一起,本文在能力谱法的基础上进行冗余度需求比指标的计算.
ATC-3对结构反应谱修正系数R定义如下.
R=RsRμRR(1)
式中,Rs、Rμ、RR分别表示结构的强度系数、延性系数和冗余度系数.
参照《公路桥梁抗震设计细则》(JTG/TB02-01-2008)计算出结构的设计反应谱,通过E2地震和E1地震作用下反应谱值之比即可求出强度折减系数系数,可以使用强度折减系数代替反应谱修正系数R.
延性系数Rμ的表达式[10](ξ=5%)为
Rμ=[c(μ-1)+1]1/c
c(T,α)=Ta/(1+Ta)+b/T}(2)
式中:T是结构自振周期、μ是结构延性比、ξ是结构阻尼比; α为拟合需求谱曲线屈服后刚度与初始刚度的比值; a、b是α的相关系数,当α=0%、2%、10%时,a=1.00、1.00、0.8,b=0.42、0.37、0.29.
冗余度系数可根据图1进行计算.图1中,Ke为能力谱曲线与E1地震需求谱曲线交点与原点的连线,表示拟合能力曲线的初始刚度; Se为能力谱曲线与E1地震需求谱曲线交点对应的谱加速度值; Sy为按能量拟合的能力曲线基底剪力屈服值转换的谱加速度值; SMT为与Se同周期的罕遇地震谱加速度值; Smax为基底剪力峰值转换的谱加速度值; dy、de、dMT、dmax分别为Sy、Se、SMT、Smax对应的谱位移值.由图1可知: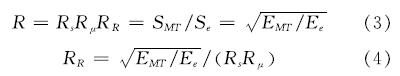
式中,EMT、Ee表示地震输入的总能量,即在弹性设计方法下单自由度体系在E2地震和E1地震中消耗的地震能量.
同时,将结构实际消耗的地震能量ED带入式(4),即可得出实际结构的冗余度系数Rr

根据图1可得出如下关系.
Ee=S2e/Ke(7a)
ED=4Sy[Sy+(Smax-Sy)/α-Smax]/Ke(7b)
μ=dmax/dy=1+(Smax-Sy)/αSy(7c)
Rs=Smax/Se(7d)
综合以上式子,得出基于能力谱法的冗余度指标r如下.
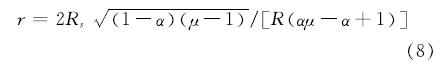
很显然冗余度指标r>1时,结构才能满足抗震需求.
目前工程界对结构鲁棒性的定义仍然没有统一,主要有以下两个定义:一是根据字面意思将鲁棒性定义为整体性和稳定性; 二是从破坏角度将鲁棒性定义为结构的易损性.本文依据定义一,将结构抗震鲁棒性定义为结构抵抗地震破坏的能力,以FEMA P695中建议的抗倒塌储备系数RCM表征,其表达式为
RCM=Sa(T1)50%/Sa(T1)(9)
式中:Sa(T1)50%、Sa(T1)分别为倒塌率概率为50%时对应的谱加速度、设计最大谱加速度; 综合两国规范,可以用我国抗震规范中E2地震代替设计考虑最大地震,式(9)可以做以下变换.
RCM=Sa(T1)50%/(α(T1)E2/g)(10)
式中:α(T1)E2为我国抗震规范中以一阶周期T1计算的E2地震下地震影响系数; g为重力加速度.
由第1、2节可知:结构抗震冗余度计算需要进行Pushover分析,而抗震鲁棒性借助IDA进行计算,考虑了地震动的随机性; 但在本质上二者是一致的,均由结构的抗震体系与材料性能所决定,均体现了结构抵御地震荷载的能力.因此,抗倒塌储备系数RCM与冗余度需求比r之间一定存在某种内在联系,可将RCM作为因变量,r作为自变量,拟合出RCM与r的关系.
本文以某高速公路3 m×30 m连续斜交桥为背景,该桥上部结构由5片T梁组成,采用C50混凝土浇筑,每跨上部结构总重645 t,全桥仅布置板式橡胶支座,支座动剪切模量G=1.2 MPa.盖梁截面为1.7 m×2.2 m,下部结构采用双柱式圆形墩(图2),墩高8 m,图中α表示斜度,特征周期为0.4 s[11].为分析斜度对连续斜交桥冗余度指标的影响,建立CSB0、CSB15、CSB30、CSB45和CSB60共5个模型(CSB后的数字代表斜度).
本文采用OpenSees软件建立全桥有限元模型(图3),其中上部结构采用弹性梁单元多梁模型模拟; 板式橡胶支座采用零长度单元模拟[4],恢复力模型取直线型; 盖梁采用弹性梁单元模拟; 桥墩采用纤维单元模拟[4],钢筋本构关系采用Steel02模型,混凝土本构关系采用Mander模型.
将中跨2#桥墩定为易损构件,以其墩顶位移达到容许位移作为极限破坏,选择能考虑高阶振型影响的加载模式[12]进行侧向力加载; 选择主梁质量中心处节点作为控制位移节点,对连续斜交桥模型进行横桥向Pushover分析,绘出5种不同斜度模型的Pushover曲线图(图4).
由1.2节可知,计算冗余度需求比r需要将能力谱曲线等效为双折线形式.以模型CSB30为例,先将其能力谱曲线与需求谱曲线绘制在同一坐标系下(图5); 然后根据结构最大横向容许位移在能力谱曲线上找到对应的谱加速度,取其60%的割线作为初始刚度线[12],取最大位移点与初始刚度线的交点作为屈后刚度直线,交点的位置根据能量相等原理确定(图5); 最后根据式(8)计算出模型CSB30的冗余度需求比r.同理得出5个模型的r(表1).
由表1可知,强度系数、位移延性及冗余度需求比均随斜度的增大而减小; 且冗余度需求比r均大于1,说明严格按照抗震规范设计的斜交桥抗震能力均达到了预设抗震目标; 横桥向地震作用下斜度越大的连续斜交桥越容易发生破坏.
由于桥址处于Ⅱ类场地,因此结合地震动三要素与ATC-63(2008)推荐的选波原则,在PEER地震数据库中选择20条硬土(Ⅱ类)场地近场记录.
合理确定桥梁结构倒塌极限并以此作为IDA分析的终止条件可以减小分析工作量,加快计算速率.本文把基于位移的损伤准则——DM准则作为IDA分析的终止准则.
以模型CSB30为例进行IDA分析.计算出模型的第一阶周期T1=1.314 s,其对应的阻尼比为5%时谱加速度Sa=0.400 g.对谱加速度Sa采用等步调幅,计算出模型CSB30在多条地震波作用下的IDA曲线(图6),图6中容许位移辅助线左侧代表结构未破坏,右侧表示结构已经发生破坏.将各地震动强度对应的结构倒塌概率绘制到同一坐标系中,并将这些数据进行拟合,最终可得出模型CSB30的易损性曲线(图7),在图中标注了倒塌概率50%所对应的地震动强度值.
通过图7可以得出模型CSB30倒塌概率为50%时对应的谱加速度Sa=0.75g,同时根据规范得出α(T1)E2=0.181g.由式(10)计算出模型CSB30的抗倒塌储备系数RCM=0.75/0.181=4.134>1,表明模型CSB30可达到预期抗震设防目标,结构抗震性能良好.
同理可得出不同模型的抗倒塌储备系数RCM的值(表2).由表3可知,连续斜交桥的RCM随斜度的增加而减小,这一结论与4.3.2节冗余度需求比r随斜度变化的规律基本一致.说明基于Pushover的冗余度分析与基于IDA的抗震鲁棒性分析均能对连续斜交桥的抗震性能进行评价.根据第3节方法,使用Origin软件拟合出抗倒塌储备系数RCM(表2)与冗余度需求比r(表1)的关系(图8).线性相关指数R2=0.980,说明RCM和r间存在较好的线性关系,可以使用冗余度理论对连续斜交桥进行抗震性能的量化评价.
图8 r与RCM的关系
Fig.8 The relationship between r and RCM
(1)连续斜交桥的斜度越大冗余度需求比r越小,结构越易损;
(2)连续斜交桥抗倒塌储备系数RCM随斜度增大而减小,斜度过大会降低结构抗震鲁棒性,减弱结构易损性;
(3)抗倒塌储备系数RCM与冗余度需求比r间存在较好的线性相关关系,说明可以使用抗震冗余度理论对连续斜交桥的抗震鲁棒性进行评价.