基金项目:“十三五”国家重点研发基金资助项目(2016YFC0700400)
第一作者:潘明众(1995-),男,硕士研究生,主要从事与建筑节能.E-mail:panmingzhong@live.xauat.edu.cn 通讯作者:刘艳峰(1971-),男,教授,博士生导师,主要从事与建筑节能与可再生能源应用.E-mail:liuyanfeng@xjd.xauat.edu.cn
(1.西安建筑科技大学 西部绿色建筑国家重点实验室,陕西 西安 710055; 2.西安建筑科技大学 建筑设备科学与工程学院,陕西 西安 710055)
(1.State Key Laboratory of Green Building in Western China, Xi'an Univ. of Arch. & Tech., Xi'an 710055, China; 2.School of Building Services Science and Engineering, Xi'an Univ. of Arch. & Tech., Xi'an 710055, China)
structural parameters; tromble wall; heat transfer; regression method
DOI: 10.15986-j.1006-7930.2020.04.018
基于热平衡法分析了集热蓄热墙的结构参数对其对流、导热传热量的影响,发现不同结构参数的集热蓄热墙的逐时传热量与其极大值的比值为高度重合的一簇曲线,进而提出对流、导热传热因子表征该簇曲线.在得到不同地区的对流、导热传热因子后,只要得到该地区结构参数与对流、导热传热量极大值的关系进而就可以得到逐时对流、导热传热量.因此,通过回归分析得到集热蓄热墙4个关键结构参数与对流、导热传热量极大值之间的多元非线性回归模型.最后对比分析了回归模型与理论计算的传热量.结果表明,各典型地区对流、导热传热量回归模型的R2分别在0.96~0.97、0.94~0.95之间,rRSME分别在0.10~0.14、0.24~0.28之间.表明回归模型能较为准确预测集热蓄热墙逐时传热量,满足工程计算精度要求,可为被动房设计提供一定指导.
Based on the heat balance method, the influence of the structural parameters of tromble wall on the convection and heat transfer is analyzed. It is found that the ratio of the hourly heat transfer capacity of the tromble wall with different structural parameters to its maximum value is highly coincident. A cluster of curves is proposed to characterize the cluster curve by convective and thermal conduction heat transfer coefficients. After obtaining the convection and heat transfer coefficients of different regions, the relationship between the structural parameters of the region and the maximum values of convection and heat transfer heat transfer can be obtained, and the convection and heat conduction heat transfer can also be obtained. Therefore, a multivariate nonlinear regression model between four key structural parameters of the heat collecting wall and the maximum value of convection and heat transfer is obtained by regression analysis. Finally, the heat transfer of the regression model and the theoretical calculation is analyzed. Rresults show that the R2 of the convective and heat transfer models in typical areas are between 0.96~0.97 and 0.94~0.95, and rRSME are between 0.10~0.14 and 0.24~0.28, respectively. It shows that the regression model can accurately predict the heat transfer capacity of the collector heat storage wall and meet the engineering calculation accuracy requirements, which can provide some guidance for passive house design.
集热蓄热墙可以显著增加室内得热,对减少负荷有着重要意义,而结构参数是集热蓄热墙传热量的主要影响因素[1].因此,掌握结构参数与传热量之间的关系是计算被动房负荷和辅助能源选择的先决条件.
高庆龙[2]利用DOE-2研究了集热蓄热墙结构参数对其传热量的影响.王德芳[3]利用反应系数法计算公共墙的非稳态导热,通过迭代得到传热量的数值解.上述方法精确度高但计算量大,难以适用于工程计算.众多学者在简化计算方法做了大量研究.
Duffin,R.J[4]提出了一个基于传递线性理论的集热蓄热墙的简易模型,而不需借助于数值模拟.W.J.Keninhs[5]曾提出过集热墙的回归公式,但其仅考虑了气候的影响.孟长再[6]等基于稳态方法分析了集热构件效率随南向日平均辐射强度变化的热性能曲线,未考虑墙体的蓄热作用.高文娟[7]等人对针对花格墙用模拟 - 回归方法得到了气象参数与集热墙传热量的多项式关系,并提出了公比项考虑了墙体蓄热特性.李元哲[8]等人根据SLR理论,给出了几种不同组合下集热蓄热墙集热效率曲线.刘加平[9]针对窑居太阳房厚重型围护结构的特点,采用D. G. Stephenson法,建立了新型窑居太阳房动态热过程的分析模型,提出了一种简洁的评价窑居太阳房室内温度瞬时分布的方法.以上文献鲜有研究设计日下集热蓄热墙的多个结构参数与其逐时向室内传热量的简化关系.
本文将通过利用Matlab求解集热蓄热墙方程组,拟得到多组结构参数对逐时传热量的数据,并基于该数据通过回归分析方法得到了结构参数与逐时传热量之间的多项式关系.为工程计算提供参考.
集热蓄热墙是由玻璃盖板、带有涂料的集热墙组成,集热墙的上下方设置有通风口.高吸收率的涂料能够吸收玻璃盖板透射过的太阳光,集热墙外表面快速升温进而加热夹层空气,并以对流的方式和室内空气形成热循环[10],本文将该部分热量称为对流传热量.集热墙同时也会以导热的方式与室内进行换热,称为导热传热量.并基于以下假设,给出了集热蓄热墙传热量的数学模型.
(1)围护结构的导热为一维导热;
(2)室内空气不参与辐射换热;
(3)忽略室内潜热变化对房间热平衡的影响.
集热墙导热传热量可用公式(1)计算,风口对流换热量可按式(2)得出[11].
导热传热量为
qi(n)=∑23j=0Y*i(j)tzi(n-j)-∑23j=0Z*i(j)ti(n-j)(1)
式中:qi(n)为n时刻通过墙体的导热传热量W/m2; Y*i(j)为该围护结构的周期传热反应系数,j取1,2,3,…,24; tzi(n-j)为n-j时刻该围护结构外表面室外综合温度(集热墙为其外表面温度),℃; ti(n-j)为n-j时刻围护结构内表面温度,℃; Z*i(j)为该围护结构周期吸热反应系数.
风口对流换热量为
Qccr(n)=(tg(n)-tm(n))/(R(n))(2)
R(n)=(((-m(n)cp)/(2Achc(n)))[exp(-(2Achc(n))/(m(n)cp))-1]-1)/((m(n)cp)/(Ac)[exp(-(2Achc(n))/(m(n)cp))-1])(3)
式中:tg(n)为n时刻玻璃外表面温度,℃; tm(n)为n时刻夹层空气温度,℃; R(n)为n时刻集热墙与房间的热阻,(m2·K)/W; Ac为集热蓄热墙的面积,m2; hc(n)为n时刻夹层空气和玻璃盖板内表面、集热墙外表面之间的对流换热系数,W/(m2·K); m(n)为n时刻的通过空气夹层质量流速,kg/s; 其中,hc(n)与集热蓄热墙尺寸结构和气流流态有关系.为了确定其值,可通过文献[11]根据公式(4~5)计算.
当m(n)为0,风口关闭(tm≥tr)时,即
hc(n)=[0.017 11(GrgPr)0.29](λg)/(lg) (4)
当m(n)不为0,风口开启(tm≥tr)时,即
{Zhc(n)=[4.9+(0.060 6((RePrDh)/(hv))1.2)/(1+0.085 6((RePrDh)/(hv))0.7)](λg)/(lg) ,
Re≤2 000
hc(n)=(0.015 8Re0.8)(λg)/(lg) , Re>2 000(5)
式中:Gr为格拉晓夫数; Pr为普朗特数; Re为雷诺数; Dh为空气夹层流道的定性尺寸,m; λg为空气导热系数,W/(m·K); lg为空气夹层厚度,m; hv为通风孔上下中心垂高,m;
集热墙导热传热量和风口对流传热量的求解需要上式方程和集热墙热平衡方程组联立,集热墙热平衡方程组包括玻璃盖板内表面热平衡方程、空气夹层热平衡方程、集热墙外表面热平衡方程、集热墙内表面热平衡方程4个方程.具体求解过程为先假定玻璃盖板内表面和集热墙外表面温度,再用公式(4~5)求解出hc(n),再把hc(n)代入集热墙热平衡方程组即公式(6~9),通过迭代直至收敛可得出tg、tm、tl、tn、hc(n)的准确值.需要说明的是由于集热墙内表面与其他内表面的辐射换热量很小,可忽略不计.
玻璃盖板内表面为
qsg(n)+hr(n)×[tl(n)-tg(n)]-hc(n)×
[tg(n)-tm(n)]-k×[tg(n)-ta(n)]=0(6)
空气夹层为
hc(n)×[tg(n)-tm(n)]+hc(n)×
[tl(n)-tm(n)]-Qccr(n)=0(7)
集热墙外表面为
qsl(n)-hc(n)×[tl(n)-tm(n)]-
hr(n)×[tl(n)-tg(n)]-qn-l(n)=0(8)
集热墙内表面为
ql-n(n)-acin×[tn(n)-tr(n)]=0(9)
式中:qsg(n)为n时刻玻璃吸收的太阳辐射,W/m2; hr(n)为n时刻集热墙外表面与玻璃内表面的辐射换热系数,W/(m2·K); qn-l(n)为n时刻集热墙内表面向外表面导热量,W/m2; ql-n(n)为n时刻集热墙外表面向内表面导热量,W/m2; ta(n)为n时刻室外空气温度,℃; Cp为空气的单位热容,J/kg·℃; qsl(n)为n时刻玻璃吸收的太阳辐射,W/m2; k-玻璃的传热系数,W/(m2·K); acin为围护结构内表面的对流换热系数,取8.7W/(m2·K); ta(n)为设计日n时刻的室外干球温度,℃; tl(n)为n时刻集热墙外表面温度,℃; tn(n)为n时刻集热墙内表面温度,℃;
集热蓄热墙结构参数是影响其传热量的重要因素,根据文献调研,选取夹层厚度、通风口面积、上下通风孔高度、公共墙的墙体构造共4个关键参数作为研究对象.选取康定、拉萨、林芝、马尔康、昌都5个地区为典型城市[12].为研究集热蓄热墙传热量对热负荷的影响,将计算热负荷的设计日作为典型日.
本研究为掌握不同结构参数组合对传热量的影响,进行了多因素多水平的交叉组合形成了多结构参数组合工况,如图1所示.对于一个地区,共44=256种工况.其中,需要说明的是,本文按照墙体的保温性能和蓄热性能选取了常见的4种类型的墙体,具体构造形式如表1所示.
利用Matlab编制求解程序,针对不同地点的组合工况进行理论计算.因为结构参数对集热蓄热墙的导热、对流传热量的影响规律不同,故分别计算出对流、导热传热量.以拉萨为例,其对流、导热传热量如图2、图3所示.由于工况较多,图中无法全部展示,故随机选取一定工况进行展示.
图3 拉萨地区部分部分组合工况的导热传热量
Fig.3 Heat conduction and heat transfer capacity of combined working conditions in Lhasa area
从上述可知,不同组合工况的对流传热量随时间的变化的规律类似,进一步利用不同工况的逐时对流传热量除以对应的极大值,可以得到一簇曲线,以拉萨为例,其结果如图4所示.
图4 拉萨地区不同工况的逐时对流传热量与其极大值的比值
Fig.4 Time-dependent convection heat supply for different working conditions in Lhasa area Ratio to its maximum
α(n)=∑numi=1(HVi(n))/(HVi-max)/num(10)
式中:α(n)为n时刻对流传热因子; HVi(n)为i工况的n时刻对流传热量,W; HVi-max为i工况的对流传热量的最大值W; num为工况数;
图5给出了各典型地区利用式(10)计算出的对流传热因子,从图中可以看出各典型地区对流传热因子与室外气象有关,但由于本文选取的地点的气象参数较为接近,故对流传热因子较为接近.
根据不同工况结构参数的传热量与极大值的关系,可以推出在得到对流传热因子后,只要得到不同工况结构参数与该工况对应的对流传热量极大值,就可以得到逐时对流传热量.多元回归是研究因变量与多个自变量的一种常用数学方法,并在建筑领域也得到广泛应用[13-14].基于第2节计算出的数据,利用Matlab软件对其进行非线性回归,建立了夹层厚度、通风孔面积、通风孔上下高度、墙体类型与对流传热量极大值的关系,回归模型设置为式(11)所示.由于对流传热量极大值的数值变化较大,采用分段拟合的方法提高准确度,本文分两段进行拟合.计算得到各典型城市的对流传热量极大值回归系数,如表2所示.
HVi-max=p1·hg3+p2·hg2+p3·hg+
p4·l+p5·tywall2+p6·tywall+p7·Aw+p8(11)
式中:hg为上下通风孔高度,m; tywall为墙体类型; l为夹层厚度,m; Aw为通风孔面积,m2.
按上述方法计算出不同地区对流传热因子和不同工况的极大值后,利用式(12)即可得到逐时的传热量.
HVi(n)=HVi-max×α(n)(12)
式中:HVi(n)为i工况逐时对流传热量,W/m2;
类似的,同样定义导热传热因子来表征不同工况的逐时导热传热量与其极大值之间的关系.另外,为了消除导热传热量跨越“0”点线所导致变化规律不同,在导热传热量加上一常数c使其都为正数.以拉萨为例,用加上常数后的逐时导热传热量除以加上常数后的传热量极大值得到一簇曲线如图6所示.
图6 拉萨地区不同工况逐时导热传热量与其极大值的比值
Fig.6 Time-dependent heat conduction of heat in different working conditions in Lhasa area Ratio to its maximum
β(n)=∑numi=1(HDi(n)+c)/(HDi-max+c)/num(13)
式中:β(n)为n时刻导热传热因子; HDi(n)为i工况的n时刻导热传热量,W/m2; HDi-max为i工况的导热传热量的极大值,W/m2; c为常数,本文取40;
从图7可以看出,典型地点的相同墙体类型的
图7 不同地点不同墙体类型的导热传热因子
Fig.7 Thermal conductivity and heat transfer coefficient of different wall types in different locations
通过多元回归得到结构参数与导热传热量极大值的多项式非线性函数关系,其回归模型如式(14)所示.在得到导热传热量的极大值后,即可利用导热传热因子将其逐时化,得到逐时导热传热量,计算公式如式(15)所示.计算得到的导热传热量极大值回归系数如表3所示.
导热传热量极大值回归模型:
HDi-max=p1·ty3wall+p2·ty2wall+p3·tywall+
p4·l2+p5·l+p6·hg2+p7·hg+p8·Aw+p9(14)
式中:hg为上下通风孔高度,m; tywall为墙体类型; l为夹层厚度,m; Aw为通风孔面积,m2.
HDi(n)=β(n)×(HDi-max+c)-c(15)
式中:HDi(n)为i工况逐时导热传热量,W/m2.
以决定系数R2、均方差RSME、均方差变化系数rRSME来评价回归模型,评价指标定义如式(16~18)所示.其中,R2反映了自变量解释因变量的程度,均方差变化系数RMSE反映预测值与真值之间的误差,定义不同范围均方差变化系数差rRSME用来反映预测模型的准确度,当rRMSE<10%时,准确度为很好; 当10%<rRMSE <20%,准确度为好,当20%<rRMSE <30%,准确度为可接受,当rRMSE> 30%,则认为不可接受[15].
表3 各典型城市导热传热量极大值回归系数
Tab.3 Regression coefficient of the maximum value of heat transfer and heat transfer in typical cities
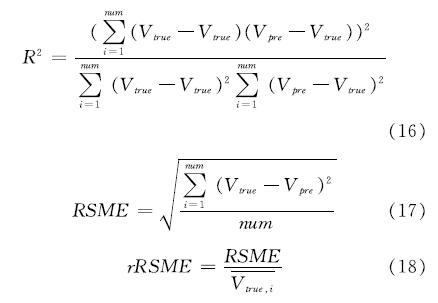
式中:R2为决定系数; Vtrue为理论计算值,W/m2; Vpre为回归值,W/m2; RSME为均方误差; rRSME为均方差变化系数; Vtrue,i^-为理论计算值的平均值,W/m2;
利用第3节所述方法,以拉萨为例,利用回归模型计算出的对流极大值乘以对流传热因子得到的对流传热量与理论计算值对比如图8所示,其回归模型的评价指标值如表4所示.其余典型城市对流传热量回归评价指标值如表5所示.
图8 拉萨地区理论与回归的逐时对流传热量比较
Fig.8 Comparison of hourly convective heat transfer between the theory and regression of Lhasa area
表5 其余城市对流传热量回归模型评价指标
Tab.5 Evaluation index of regression model of convective heat transfer in other cities
从图8和表4、5可以看出,对流传热量的回归模型的决定系数(R2)为0.97,表明所选变量夹层厚度、通风孔面积、上下通风孔高度、公共墙类型与对流传热量极大值相关性较好,且能较好解释其值.回归值绝大部分落在误差线为“0”所对应参考线左右,均方差变化系数(rRSME)范围在0.12~0.14,表明该模型的准确性较好.
类似的,图9和表6给出了拉萨地区导热传热量理论计算值与回归值的对比和其模型评价指标值.其余典型城市导热传热量回归评价指标值如表7所示.
表6 拉萨地区导热传热量回归模型评价指标
Tab.6 Evaluation index of thermal conductivity and heat transfer quantity in Lhasa area
图9 拉萨地区导热传热量理论计算值与回归值对比
Fig.9 Comparison of theoretical calculation values and regression values of heat conduction and heat transfer in Lhasa area
表7 其余典型城市导热传热量回归模型评价指标
Tab.7 Evaluation index of regression model of heat conduction and heat transfer in other typical cities
从图9、表6、7可知,各典型城市导热传热量回归模型rRSME范围在0.24~0.28,R2在0.90~0.92,表示选取夹层厚度、通风孔面积、上下通风口高度、公共墙类型作为影响传热量的关键参数,利用公式(14)计算出的导热传热量极大值,进而利用导热传热因子进行逐时化得到导热传热量的方法准确度较高.
本文基于热平衡原理,通过Matlab编制了集热蓄热墙传热量求解程序,并提炼出了对流、导热传热因子,进一步分析出结构参数与对流、导热传热量极大值的关系,最终建立并评价了夹层厚度、通风孔面积、上下通风孔高度、公共墙类型与对流、导热传热量的回归模型,研究结果表明:
(1)不同结构参数的逐时对流传热量与其极大值之比随时间变化的趋势几乎相同,因此,提出对流传热因子表达逐时对流传热量与其极大值之间的关系; 类似的,提出导热传热因子表达逐时导热传热量与其极大值之间的关系,但与对流传热因子不同是导热传热因子与墙体类型有关;
(2)各典型城市对流、导热传热量预测模型的rRSME范围在0.10~0.14、0.24~0.28,R2在0.96~0.97、0.90~0.92.表明以夹层厚度、通风口高度、通风口面积、墙体类型4个结构参数预测出对流、导热传热量极大值,再通过对流、导热传热因子将其逐时化的方法能够准确有效重现其逐时传热量的理论值;
(3)本文给出了集热蓄热墙结构参数与其传热量之间的多项式关系,具有计算简单的优点,适用于被动构件的设计制造和被动房热负荷的工程计算.