基金项目:国家自然科学基金青年科学基金资助项目(51708446); 青海省高原绿色建筑与生态社区重点实验室开放基金计划资助项目(KLKF-2018-007); 陕西省重点研发计划项目重点产业创新链(群)(2020ZDLNY06-03)
第一作者:赵 祥(1975-),男,博士,副教授,主要从事结构振动控制研究.E-mail:441937590@qq.com 通信作者:高永苗(1995-),女,硕士研究生, 主要从事结构振动控制研究.E-mail:345273078@qq.com
(1.西安建筑科技大学 土木工程学院, 陕西 西安 710055; 2.青海省高原绿色建筑与生态社区重点实验室, 青海 西宁 810008)
变阻尼式TMD; 力学性能试验; 遗传算法; Simulink仿真; 减震效果
(1.School of Civil Engineering, Xi'an Univ. of Arch. & Tech., Xi'an 710055, China; 2.The Key Lab of Plateau Building and Eco-community in Qinghai, Xining 810008, China)
variable damping TMD; mechanical test; genetic algorithm; Simulink simulation; damping effect
DOI: 10.15986/j.1006-7930.2020.06.004
研发了一种新型变阻尼式TMD,阐述了它的构造设计及工作原理,通过对其进行的力学性能试验,研究了与该减震装置组成成分相关的三个参数(质量、刚度和液体黏度)变化时对其力学性能的影响.试验结果表明:当该减震装置组成部分相应的刚度、质量和液体黏度增大时,该减震装置对结构施加的等效阻尼力也随之增大,而且其在大震时对结构的减振效果更好.接着利用遗传算法,对该减震装置的阻尼系数,频率比,限制位移(相对结构的最大许可位移)等参数进行了优化分析,并得出了它们的最优取值.最后,为了研究该变阻尼式TMD对结构的减震效果,利用Simulink工具对未安装和安装该变阻尼式TMD的弹性单自由度结构进行了仿真分析; 仿真结果表明:该变阻尼式TMD能够很好的控制结构的加速度和位移响应,且随着地震动幅值的增大,它的减震效果也逐渐增大,这与力学性能试验的结果较好吻合.
In this paper, a new type of variable damp TMD is developed. Its structure design and working principle are described. Through mechanical properties test, the effects of three parameters(mass, stiffness and liquid viscosity)related to the components of the damping device on its mechanical properties are studied. Test results show that when the corresponding stiffness, mass and liquid viscosity of the components of the damping device increase, the equivalent damping force exerted by the damping device on the structure will also increase, and the effect of the damping device on the structure will be better in large earthquakes. Then, the parameters such as damping coefficient, frequency ratio and limited displacement(maximum allowable displacement relative to the structure)of the damping device are optimized and analyzed by genetic algorithm, and their optimal values are obtained. Finally, in order to study the effect of the variable damp TMD on the structure, Simulink tool is used to simulate and analyze the elastic single-degree-of-freedom structure which is not installed or installed with the variable damp TMD. Tesults show that the variable damp TMD can control the acceleration and displacement response of the structure well, and with the increase of the amplitude of the ground motion, its damping effect increases gradually, which is in good agreement with the results of the mechanical properties test.
调谐质量阻尼器( Tuned Mass Damper,简称TMD)由质量块、弹簧和阻尼系统组成,通过调整 TMD 的自振频率,使其接近主体结构的被控频率,当主体结构受迫振动时,TMD 随之产生与主体结构相反的运动并施加反作用力于主体结构,输入结构的振动能量通过调谐质量阻尼器逐步消散,从而控制结构的振动[1].目前,关于TMD在抗风方面的研究也取得了一系列的研究成果.Mcnamara等[2]采用单自由度结构模型,基于等效阻尼比的概念研究了TMD在高层建筑中的抗风问题; Gu等[3]通过数值研究表明TMD能够有效地降低大跨度桥梁的风致振动.就TMD在减小结构地震响应方面,国内外学者也进行了许多数值分析和试验研究.Wirsching和Yao[4]基于5层和10层的钢框架结构,首次验证了TMD控制结构地震响应的有效性.随后,Dong、Ohno、Jagadish、袁俊和王虎长等[5-10]人均研究了TMD对地震反应的控制效果,结果表明TMD能够有效地降低结构的地震反应.TMD的基本理论已经成熟,但是TMD在工程中的应用仍有许多问题需要面对,比如说,TMD质量的选取,弹簧刚度K的大小以及阻尼比的确定等.这些问题就涉及TMD参数的优化分析处理.针对这些问题,国内外专家学者进行了广泛地研究.Den Hartog等[11]通过分析在正弦激励下无阻尼结构的动力响应,建立了TMD最优参数的解析式,Warburton[12]以列表的形式给出了在特定质量比下,结构在各种外界激励下各参数的优化计算公式.尽管TMD能够有效地降低结构的振动响应,但是其最大的局限性是仅适合于窄频带的外部激励,当因某种原因主结构的自振频率同TMD自振频率产生偏离时,则TMD将会担当放大器的角色,使得主结构的振动响应增大.研究者们尝试着将非线性弹簧引入TMD以改善它的窄频带特性.Roberson[13]研究了无阻尼非线性动力吸振器,分析发现非线性弹簧的存在能够加宽动力吸振器的调谐带宽; 部分学者通过在主结构中装设多个频率不同的 TMD 子结构(MTMD),分别控制不同频段的外界激励以改善 TMD 的调谐频带.另外李春祥等[14]人也对 DTMD、MTMD 的动力特性、设计参数、 敏感性等进行了研究.刘纲等[15]采用改进了的NSGA-Ⅱ算法分析在阻尼器个数保持不变情况下的最优布设位置.
总体来看,TMD安装便捷、性能可靠且减震效果显著,将其用于结构的减震控制中是可行的.但目前国内外专家学者关于TMD的研究大多数聚焦在TMD的位置、数量、参数等方面的理论研究,进而忽略了从TMD装置本身的改进来提高其工作性能,并且针对TMD减震控制方面的力学性能试验研究有所欠缺.因此,本文提出一种新型的变阻尼式TMD减震控制装置,并对该TMD装置的相关参数进行了力学性能试验,利用遗传优化算法,对该TMD的阻尼系数,频率比,限制位移等参数进行了优化分析,并同传统TMD进行了对比分析; 同时采用MATLAB软件中的Simulink工具箱建立了主系统-变阻尼式TMD减震体系的仿真计算模型,并对一弹性单自由度结构进行了仿真分析.结果表明在不同地震作用下该变阻尼式TMD具有很好的减震效果.
针对当前传统 TMD 的不足之处,设计并制作了一种新型变阻尼式 TMD,如图 1所示,腔体示意图如图2所示.
该装置包括质量块、弹簧、牛眼轴承、底板、腔体1、出油口、丝杠1、挡板1、腔体2、挡板2、丝杠2、导轨和进油口等部分.丝杠1与质量块两侧固定连接,质量块通过牛眼轴承与导轨相接; 质量块的导向工作由导轨和丝杠1完成,牛眼轴承具有滑动作用,确保质量块能够顺畅的左右滑动; 质量块和腔体1通过丝杠1相连,导杆上装有刚度为K的弹簧,通过调节质量块的质量M和弹簧的刚度K可以实现变阻尼式TMD的调谐,进而达成对主体结构的减振控制; 腔体1和腔体2用来装液体,腔体内部设置扇叶,螺母连接扇叶和丝杠,同时丝杠也有改变运动方向的作用,即质量块水平运动通过丝杠变为竖向转动,扇叶通过螺栓和轴承固定在一块,而轴承则套装在丝杠上,从而可实现扇叶的转动,扇叶在液体中的转动用来消耗主体结构传递来的能量,进而起到为TMD提供阻尼的作用; 腔体上设了进油口与出油口2个孔洞,可以实现液体的更换; 初始状态下,丝杠1和丝杠2间的间隔距离为ue,该距离为位移临界阈值,当减震装置的位移小于ue时,只有腔体1提供阻尼,当位移大于ue时,丝杠1移动到丝杠2处,并且通过挡板1带动丝杠2一起转动,此时腔体1与腔体2共同提供阻尼; 挡板2起支撑丝杠2的作用.
该装置的工作原理可叙述为:由于外界环境的激励,质量块产生水平振动,从而压缩弹簧,而弹簧经过腔体和底板相接,进而将质量块振动导致的惯性力通过上述弹簧的弹性恢复力反作用于主体结构,可以对结构的振动起到一定的控制作用,使结构的动力响应得到衰减; 同时,质量块的水平振动由丝杠变为扇叶的竖向转动,而腔体内充满阻尼介质,可以对阻尼器实现滞回耗能; 阻尼介质在腔体内部流动时与扇叶之间产生相互作用,使介质的动能转化为热能,从而消耗地震输入的能量,而该装置转化动能为热能的主要途径为液体的摩擦耗能.
对于变阻尼式TMD的阻尼力可理解为:在外荷载作用下,质量块的水平运动将带动叶轮以一定角速度在腔体内旋转,而叶轮扇叶的左右两侧将产生压力差,使得液体在扇叶与腔体的间隙中流动,从而产生阻尼力,其阻尼系数可根据流体力学相关理论来进行推导.
对于扇叶与腔体之间的流体流动问题,与两平行板之间的流体流动问题相似,故可借鉴其推导原理来进行分析.从腔体和扇叶所形成的间隙流场取一微元体如图3所示.
对该微元体列沿X方向的平衡方程,可得
(dp)/(dx)=(dτ)/(dy)(1)
其中,p为压强,τ为剪应力,dp/dx沿X方向为常数,则
(dp)/(dx)=(Δp)/l(2)
其中,Δp为两平行板间进口与出口压力差,l为扇叶的宽度.在间隙流动中,流体的流速和剪应力关于间隙中面对称,同时由式(1)和式(2)可得
τ=(Δp)/lx(3)
腔体内部阻尼介质的本构方程为:
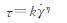 (4)
(4)
其中:k为稠度系数,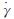 为剪切应变率,η为流动指数.当η<1时,该阻尼介质为剪切稀化流体; 当η>1时为剪切稠化流体; 当η=1时,为牛顿流体.由式(3)~(4),又有边界条件y=±h/2; u=0可得
为剪切应变率,η为流动指数.当η<1时,该阻尼介质为剪切稀化流体; 当η>1时为剪切稠化流体; 当η=1时,为牛顿流体.由式(3)~(4),又有边界条件y=±h/2; u=0可得
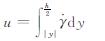 (5)
(5)
故流过两平板的流体的流量为
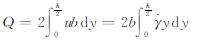 (6)
(6)
综合上式以及边界条件可得
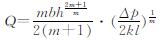 (7)
(7)
Q为阻尼缝隙的总流量,等于单位时间内一侧叶片扫过的扇面面积与叶片宽度的乘积:
Q=1/2(R2-r2)ωl(8)
则流体的阻尼力
F=ΔPAp(9)
故
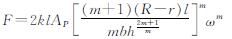 (10)
(10)
式中,l为扇叶宽度; b为扇叶厚度; r为转轴直径; R为扇叶顶端至转轴中心半径; ω=2πυ/s为叶轮转动角速度,其中υ为阻尼器的速度,s为丝杠的行程; h为阻尼缝隙宽度.
因此, 可得变阻尼式TMD中的阻尼系数c为
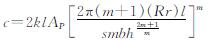 (11)
(11)
变阻尼式TMD的工作原理如图4所示,x、xd分别为主系统和阻尼器相对于地面的位移值,设u=xd-x为阻尼器相对于主系统的位移,则变阻尼式TMD的运动方程为
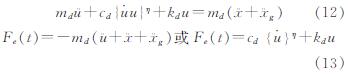
其中,Fe(t)为TMD附加给平台的等效阻尼力,x¨为变阻尼式TMD系统所在楼层相对于地面的加速度; md、kd、cd分别为变阻尼式TMD系统的质量、刚度和阻尼系数; 其中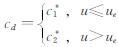 ,ue为临界位移; η为流动指数,当η=1时,该变阻尼式TMD系统为线性系统,否则为非线性系统; xd为变阻尼式TMD系统相对于地面的位移.由式(12)可知,当变阻尼式TMD系统相对于结构的位移小于等于临界位移ue时,该变阻尼式TMD系统提供一种控制力; 当变阻尼式TMD系统相对于结构的位移大于临界位移ue时,该变阻尼式TMD系统将提供另外一种控制力,以控制结构的地震响应,使其降至所需状态.
,ue为临界位移; η为流动指数,当η=1时,该变阻尼式TMD系统为线性系统,否则为非线性系统; xd为变阻尼式TMD系统相对于地面的位移.由式(12)可知,当变阻尼式TMD系统相对于结构的位移小于等于临界位移ue时,该变阻尼式TMD系统提供一种控制力; 当变阻尼式TMD系统相对于结构的位移大于临界位移ue时,该变阻尼式TMD系统将提供另外一种控制力,以控制结构的地震响应,使其降至所需状态.
新型变阻尼式 TMD 的各部分可分别加工,然后通过简单组装即可成型.为了研究该变阻尼式TMD的质量、刚度和液体的黏度这三个参数对它的力学性能的影响,设计了7组变阻尼式TMD,它们的具体参数如表1所示.并将其置于WS-Z50小型精密振动台上进行动力特性测试及振动台试验.如图5所示,试验中的测点共有2处,第一测点采用电荷加速度传感器置于振动台台面处,第二测点采用ICP加速度传感器置于TMD质量块上.
选取加速度峰值为50 gal的白噪声作为激励沿X方向输入,扫频时间为30 s,采样频率为1 000 Hz,以获得7组变阻尼TMD 的自振频率,而阻尼比则采用半功率带宽法来确定,计算公式如下.
ζ=(f2-f1)/(2f)×100%=(Δf)/(2f)×100%(14)
其中, f为装置的自振频率; f1、f2为相应自振频率两侧自振频率对应幅值的 1/21/2倍时的扰动频率.得到7组TMD的自振频率和相应的阻尼比如表2所示.然后再选取加速度峰值分别为70 gal、100 gal、200 gal、300 gal、400 gal、500 gal的Kobe波,按照公式(13)测定7组变阻尼式TMD的等效阻尼力.
由图6可以看出,在Kobe波作用下,TMD装置的等效力响应区间与实际地震输入基本一致,在加载前10 s内,由于地震加速度较小,等效阻尼力也很弱; 当时间处于10~25 s区间时,等效力出现响应并达到峰值,由于Kobe波在15.17 s时加速度达到了峰值,此时TMD最大等效力也出现在15 s左右; 随着地震波强度减弱,TMD等效力也随之逐渐减小并趋于平稳直至地震激励结束.当地震输入加速度峰值分别为70 gal、100 gal、200 gal、300 gal、400 gal、500 gal时,测得S4变阻尼式TMD的等效阻尼力峰值分别为0.633 3 N、1.026 9 N、1.214 6 N、2.584 2 N、3.328 1 N、3.452 5 N,由此可知,变阻尼式TMD在地震波的作用下,等效阻尼力随地震加速度峰值加速度增大而增大.图7为7组变阻尼式TMD的等效阻尼力随地震加速度变化的关系图.通过上述图表可知:在相同加速度峰值的地震作用下,当变阻尼式TMD的液体组合黏度,刚度和质量增大时,其等效阻尼力也随之增大,且随着地震加速度峰值的增加,它们的等效阻尼力增长幅度也相应增大,这表明该变阻尼式TMD在大震时减振效果更好.
为了研究变阻尼式TMD的阻尼系数c*、频率比f和限制位移D(相对于主系统的最大位移值)等参数对受控系统的动力响应的影响规律,并寻找最优值,以获取对受控系统的最佳控制效果.采用遗传算法,选取受控系统的最大位移作为优化目标函数,即:
J=max(x)(15)
其中,J为目标函数值,x为地震作用下主系统的位移响应.
本文的目标函数可定义适应度函数为
minf,ξ,D J(f,c*,D)(16)
s.t.:c*min≤c*≤c*max
fmin≤f≤fmax
Dmin≤D≤Dmax
取单自由度主系统的参数为:单位质量,周期2.6 s,阻尼比0.05,分析模型如图8所示.
参考Den Hartog[11]给出的单自由度结构TMD最优频率比和阻尼表达式,取频率比的下限值fmin和上限值fmax分别为0.1和1.2,阻尼系数的下限值c*min和上限值c*max分别为0和4; 限制位移的下限值Dmin和上限值Dmax分别为0 m和1.0 m; 质量比μ分别为0.01、0.02、0.05、0.1、0.2、0.3、0.4.地震动输入采用加速度峰值为0.4 g的El-Centro波,时长为54 s.用遗传算法进行计算时,初始种群取为40个,遗传代数为200代,交叉概率为0.8,变异概率为0.05.同时引入传统TMD,并作对比分析,计算结果分别如表3和4所示.
图9是最优个体收敛进程图,由图中可以看出,该算法能够在较短的进程内趋近于最优值,能够从侧面反映出算法的稳定性和收敛性较好.从表3和表4可以看出,变阻尼式TMD和传统TMD的优化结果同质量比的影响较大,随着质量比的增加,最优减震效果显著增强,且变阻尼式TMD的减震效果高于传统TMD; 同时两者的最优频率比均呈现逐渐减小趋势,但变化范围均处于1附近,两种TMD的阻尼系数均随着质量比的增大呈现逐渐增大的趋势,同时,变阻尼式TMD的最优阻尼系数c*1均小于最优阻尼系数c*2.
图 10为不同质量比下,变阻尼式TMD与传统TMD对受控系统的最优减震效果的对比图.由图中可知,随着质量比的增加,两种型式TMD减震效果逐渐增强,当质量比较小时,两种型式TMD的减震效果比较接近,且均较小,由表3和表4可知,当质量比为0.01时,两种型式TMD减震效果均仅有6%; 随着质量比的增加,变阻尼式TMD的减震优势则逐渐凸显出来,较传统TMD而言,变阻尼式TMD的减震效果可提高15%左右; 随着质量比的增加,最优减震效果增长的趋势逐渐降低,虽然质量比越大减震效果越明显,但是质量比过大,势必造成子结构的质量增加,这将给施工造成不便.当质量比为0.1时,10图中出现拐点,最优减震效果的增加趋势逐渐趋近于平缓,综合考虑,建议取阻尼器的最优质量比为0.1为佳.
图 10 两种TMD优化结果对比图
Fig.10 Comparison of optimization results between traditional TMD and variable damping TMD
图 11为质量比为0.1时,受控系统的位移最大值与变阻尼式TMD的限制位移的关系变化图,由图中可以看出,随着限制位移的增加,主系统的最大位移呈现先降低后增加,最后呈现平直段的现象,这表明随着限制位移的增加,变阻尼式TMD对受控系统的位移最大值的减震效果呈现先增加后降低的趋势,平直段主要是由于限制位移超过变阻尼式TMD运动的最大位移所致.因此,存在一个最佳限制位移,使得变阻尼式TMD的减震效果达到最优,在对变阻尼式TMD设计制作之前,应对其进行数值分析,将其最优限制位移寻找出来.
数值分析采用的模型为一单自由度结构模型,假设主系统的质量为1 kg,基本周期为2.6 s,阻尼比为0.05,变阻尼式TMD的参数采用上述质量比为0.1时的各项最优参数,即最优频率比f为0.954,最优阻尼系数c*1为2.067 7 N/(m·s-1),最优阻尼系数c*2为3.279 6 N/(m·s-1),最优限制位移D为0.565 m.变阻尼式TMD减震体系Simulink仿真模型如图 12所示,该模型由主系统模块,变阻尼式TMD模块,控制力模块和能量模块四大子系统构成.输入x¨g,CF分别表示为地震加速度和被动控制力; 输出M-A,M-V,M-D分别为主系统相对于地面的加速度,速度和位移; T-V和T-D分别为变阻尼式TMD相对主系统的速度和位移; ETT为变阻尼式TMD所转移能量; EKT,EST和ECT分别是主系统的动能、应变能和阻尼耗能.选用El-Centro波作为输入的地震波激励,其加速度峰值分别设置为0.07 g,0.2 g和0.4 g,最后对比分析主系统在变阻尼式TMD的减振控制作用(有控状态)下和无TMD的控制(无控状态)下的动力响应和能量变化.
由图 13可知,该变阻尼式TMD能够很好的控制主系统的位移和加速度响应.但是在地震动作用前期,变阻尼式TMD的控制效果不是特别明显,这主要是由于在前5 s作用下,该变阻尼式TMD并没有启动,对主系统的控制效果不明显.从图 14中可知,随着地震动幅值的增大,主系统的位移和加速度均呈现增大的趋势,且两线段间的竖直距离呈现同样的变化规律,这表明,随着地震动幅值的增加,该变阻尼式TMD对主系统的减震效果逐渐增大; 同时,即使在小震作用下,变阻尼式TMD的减震效果也能达到20%作用,这充分体现了该变阻尼式TMD的优越性.变阻尼式TMD在不同地震动幅值作用下的减震效果如表5~6所示.由表5~6可知,变阻尼式TMD能够有效地降低主系统在地震作用下的动力响应,且能够取得较好地减震控制效果.当地震动的加速度幅值分别为0.07 g、0.2 g、0.4 g时,结构的位移分别降低了19%、30%、46%; 此时,变阻尼式TMD对主系统的加速度的减振效果分别为22%、34%、42%.
表6 不同幅值下加速度减震效果(m/s2)
Tab.6 Acceleration damping effect under different amplitudes(m/s2)
在不同幅值的El-Centro波的激励下,无控状态和有控状态下主系统的能量平衡示意图如图 15所示.由图可知,对于弹性单自由度系统而言,主系统在地震作用下吸收的能量,转化为动能,应变能,阻尼耗能,其中动能和应变能仅参与受控结构的能量转换,但并不耗散地震能量,主系统的能量主要依靠阻尼耗散.当主系统附加上变阻尼式TMD后,可明显看到地震输入至主系统的能量得到减少,这主要是因为主系统由原来的单纯依靠自身阻尼消耗能量,转变成依靠自身阻尼和变阻尼式TMD两种方式来消耗能量,故结构的各能量成分得到减少,从而保护了主系统.
本文在传统TMD的基础上研发了一种新型变阻尼式TMD,对其进行了力学性能试验,基于遗传算法对该减震装置的相关参数进行了优化计算,并与传统TMD进行了对比分析,最后利用Matlab/Simulink 工具箱对一弹性单自由度结构体系进行了减振仿真分析,得到了以下结论:
(1)力学性能试验表明:当变阻尼式TMD的质量保持不变时,该减震装置对主系统输出的等效阻尼力随着装置的刚度和液体黏度的增大而增大; 随着地震动幅值的增加,其等效阻尼力增长幅度也相应增大,故该减震装置在大震时的减振效果更好.
(2)参数优化分析表明:随着质量比的增加,该减震装置的最优频率比逐渐降低,而最优阻尼系数则逐渐增大.在质量比相同的情况下,随着限制位移的增大,该变阻尼式TMD的对结构的减震效果是先增大后降低的.
(3)仿真计算结果表明:该变阻尼式TMD能够很好的控制结构的加速度和位移响应,且随着地震动幅值的增大,变阻尼式TMD的减震效果也增大.