10个试件破坏过程基本相似,均发生弯曲破坏.以HSC-S2-3为例,试验过程中,随着水平荷载的增大,先在受拉区出现水平开裂,随着水平荷载的继续增加,根部出现竖向受压裂缝,纵向钢筋开始出现屈服; 当采用位移控制时,柱根角部保护层开始脱落,随着位移控制的加大,直至7Δ_y时,柱根部保护层已经大面积剥落,钢筋外露,且推拉两方向的位移角已达1/24.7和1/22.6.加载停止后,试件仍具有一定承载力,荷载下降至峰值的68.5%且较为稳定,核心混凝土仍未明显压碎剥落,体现了较好的延性性能.试件HSC-S2-3的破坏形态及裂缝分布如图4所示.

图4 试件HSC-S2-3裂缝破坏图
Fig.4 Failure mode of specimen HSC-S2-3

将各试件荷载-水平位移滞回曲线上每次循环的峰值点(各点的荷载、位移取对应循环的正、反方向绝对值的平均值)连接起来的包络线称为其骨架曲线,其形状可以明确地反映出结构或构件的强度、变形和延性等抗震性能,也可以反映出构件的屈服点、最大荷载点和极限点等特征点.

图5是在不同配箍特征值下发生弯曲破坏柱的骨架曲线,由图可见:随着配箍特征值的减小,骨架曲线的上升段变化不大,下降段明显变陡,延性降低.图6为轴压比对骨架曲线的影响,由图可知:轴压比较大的试件,到达峰值后,骨架曲线迅速下降,无明显平直段,且极限承载力较小,延性降低.

图5 配箍特征值的影响
Fig.5 Influence of the stirrup characteristic value

图6 轴压比的影响
Fig.6 Influence of axial pressure ratio

主要试验结果如表2所示,其中V_c和Δ_c分别为试件的开裂荷载及开裂位移; V_y和Δ_y分别为试件纵筋屈服的屈服荷载及屈服位移; V_p和Δ_p分别为试件峰值荷载及其对应的峰值位移; V_u为试件发生弯曲破坏时的极限荷载,Δ_u为V_u相对应的极限位移μ_Δ为试件发生弯曲破坏时的位移延性系数,按μ_Δ=Δ_u/Δ_y计算.

表2 各试件试验结果
Tab.2 Test results of columns failed

试验表明,在水平荷载作用下,弯曲破坏柱荷载-位移曲线可以分为4个阶段:(1)开始加载到混凝土柱出现弯曲裂缝,此阶段可以认为试件处于弹性状态;(2)试件开裂至纵向钢筋屈服,此阶段塑性铰区域混凝土进入非线性工作状态;(3)从纵向钢筋屈服至柱达到峰值承载力;(4)从峰值点至弯曲破坏,此阶段钢筋进入塑性变形阶段,塑性铰区域混凝土进入非线性工作状态,经过一段变形后箍筋屈服,试件发生弯曲破坏.针对上述过程,荷载-变形曲线有4个特征点,即开裂点C、屈服点Y、峰值点P和极限点U.因此,本文提出简化的荷载-位移骨架曲线模型,该模型由4个直线段组成(如图7所示),确定了4个特征点相应的荷载及位移,就可建立起试件的骨架曲线.

图7 骨架曲线模型
Fig.7 Skeleton curve model

为了方便分析,本文对骨架曲线模型做出了如下假定:

(1)试件开裂前混凝土和钢筋是弹性工作状态(OC段);(2)从混凝土开裂至纵向钢筋屈服,塑性铰区域的混凝土处于弹塑性工作状态(CY段);(3)纵筋屈服到试件发生破坏,塑性铰区域混凝土处于理想弹塑性工作状态(YP、PU段),钢筋处于理想塑性工作状态,塑性铰区域外混凝土和钢筋处于弹性工作状态;(4)柱截面符合平截面假定,且发生适筋破坏,在混凝土开裂后退出工作,受拉区混凝土不参与工作.

图7中,各阶段水平荷载计算公式如下

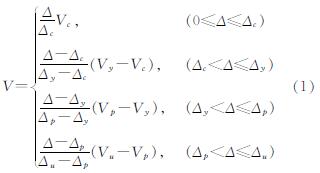
式中:V为位移Δ对应的水平荷载; V_c、V_y、V_p和V_u分别是开裂荷载、屈服荷载、峰值荷载和极限荷载,Δ_c、Δ_y、Δ_p和Δ_u分别是开裂位移、屈服位移、峰值位移和极限位移.

HSC柱在水平荷载作用下的总水平位移包括弯曲位移Δ_f、剪切位移Δ_v和柱墩内纵向受力钢筋的粘结滑移位移Δ_s,如图8所示.在弯曲破坏时剪切位移与粘结滑移位移占20%左右,甚至更多^[8].因此,剪切位移和粘结滑移位移的计算是弯曲破坏柱的主要计算内容之一.

图8 柱的水平位移
Fig.8 Components of horizontal displacement

在水平荷载的作用下,柱截面受拉侧边缘混凝土应变达到极限拉应变时ε_tmax,此时柱出现裂缝,此时的假定塑性区高度为受拉区高度的一半,且受压区混凝土仍是弹性工作阶段^[9].则此时的开裂弯矩为

M_cr=[(0.7+(120)/h)γ_mf_t+N/(A₀)]W_o (2)

由GB 50010-2010《混凝土结构设计规范》^[7]知h≤400,取h=400,截面抵抗矩塑性系数γ_m=1.55,W₀=(I₀)/(h-x_cr),I₀=(b(h-x_cr)³)/3+(bx³_cr)/3+n'A_s(h₀-x_cr)²+n'A'_s(x_cr-a')²,A₀=bh+(n'-1)A_s+(n'-1)A'_s.

换算成截面中性轴至受压边缘的距离x_cr为

x_cr=(0.5bh²+n'A_sh₀+n'A'_sa')/(bh+n'A_s+n'A'_s)

式中:n'为钢筋弹性模量与混凝土弹性模量之比,既n'=E_s/E_c,其中:E_s=2.0×10⁵ N/mm²; E_c=(0.45(f_cu,k)^1/2+0.5)×10⁴ N/mm²,参考清华大学许锦峰^[10]给出的高强混凝土的试验规律; f_t为混凝土轴心抗拉强度值; N为轴压力; A₀为换算截面面积; W₀为换算截面A₀对受拉边缘的弹性抵抗矩.

根据结构力学原理,HSC柱顶点弯曲位移Δ_f与开裂曲率φ_cr的关系为

Δ_f=1/3φ_crl²(3)

式中:φ_cr为开裂荷载,可根据φ_cr=M_cr/(E_cI₀)求得,l为柱长.

根据弹性力学原理,水平荷载产生的剪切位移为

Δ_v=(V_crl)/(GA)(4)

式中:V_cr为混凝土开裂时的水平荷载; A为柱的截面面积; G为混凝土剪切模量G=0.4E_c.

HSC柱开裂后,纵筋相对于底座伸长,引起钢筋相对混凝土的粘结滑移,则钢筋粘结滑移引起的柱端水平位移Δ_s,采用Sezen模型^[11]计算

Δ_s=(ε_sσ_sd_bl)/(8u_b(h₀-x_cr))(5)

式中:Δ_s为受拉钢筋应变; σ_s为受拉钢筋应力,且σ_s=E_sε_s; d_b为纵筋直径; u_b为纵筋弹性变形时产生的均匀粘结应力,取1.0(f_ck)^1/2,f_ck=0.88α_c1α_c2f_cu,k,式中:α_c1为棱柱体抗压强度与立方体抗压强度之比,对混凝土强度等级为C50及以下的取α_c1=0.76,对C80取α_c1=0.82,中间按线性插值计算; α_c2为高强度混凝土的脆性折减系数,对C40及以下取α_c2=1.00,对C80取α_c2=0.87,中间按线性插值计算; 0.88为考虑实际构件与试件混凝土强度之间的差异而取用的折减系数.

柱顶端的水平位移为弯曲位移、剪切位移和柱端滑移位移之和,即

Δ_cr=Δ_f+Δ_v+Δ_s(6)

考虑二阶弯矩影响,开裂荷载可表示为

V_cr=(M_cr-NΔ_cr)/l(7)

根据截面轴力平衡和弯矩平衡条件建立计算式,解得纵向钢筋屈服时的弯矩M_y和曲率φ_y.

假定HSC柱开裂到纵向钢筋屈服,荷载-位移为线性关系,考虑到塑性铰区域的变形,则弯曲位移Δ_f^[12]为

Δ_f=1/3φ_crl²+(φ_y-φ_cr)l_p(l-0.5l_p)(8)

式中:l_p为试件塑性铰区高度,塑性铰长度基于柱位移和曲率的方法计算所得^[13].

考虑钢筋混凝土柱的受拉纵筋达到屈服前,一般不发生剪切裂缝,因此认为纵筋受拉屈服前的剪切为弹性剪切,即假定钢筋混凝土柱的弹性模量及剪切模量为常数,k_v为有效剪切面积系数( 矩形柱为5/6,圆形柱为0.85)^[14]; G为剪切模量,Park^[15]认为当没有剪切斜裂缝时,可近似取G =0.4E_c,E_c为混凝土的弹性模量.则

Δ_v=(V_yl)/(k_vGA)(9)

HSC柱钢筋屈服时构件钢筋的滑移引起的Δ_s采用式(5)进行计算.将式(8)、(9)和(6)代入式(7)中计算柱钢筋屈服时的位移和荷载.

根据平衡条件,建立峰值点时的弯矩M_p和曲率φ_p的计算公式如下所示.

M_p=α₁f_yA_s(h₀-a'_s)+βN(h/2-a'_s)(10)

φ_p=(ε₀+ε_s)/(h₀)(11)

式中:α₁为柱荷载计算系数,受拉侧配筋率小于等于0.8%时取1.2,大于等于1.0%时取0.8,中间按线性插值计算; β为轴力调整系数,当轴压比小于等于0.3时取1.3,大于等于0.5时取1.4,中间按线性插值计算; ε₀按规范^[7]取ε₀=0.002+0.5(f_cu,k-50)×10^-5; ε_s为达到峰值荷载时的钢筋应变.

则根据假设荷载-位移为线性关系,考虑塑性区域的变形,其弯曲位移Δ_f为

Δ_f=1/3φ_yl²+(φ_p-φ_y)l_p(l-0.5l_p)(12)

式中:l_p的取值与式(8)相同.

用纵筋、箍筋和45°的混凝土斜压杆组成的桁架模型来考虑塑性铰区的抗剪刚度K,根据则其峰值剪切位移为

Δ_v=(V_pl)/(k_vGA)+(V_pl_p)/K(13)

式中:K=(ρ_sv)/(1+4n'ρ_sv)E_sbh,其中ρ_sv为配箍率,n'为弹性模量之比.

钢筋粘结滑移引起的位移的Δ_s采用(5)进行计算,将式(12)、(13)和(6)代入式(7)中计算柱荷载达到峰值时的位移和荷载.

极限位移取荷载下降至峰值85%时所对应的荷载,因此,有

V_u=0.85V_p

弯曲破坏位移Δ_u用位移延性系数μ_Δ表示,由图9知弯曲破坏的位移延性系数与配箍特征值成正比,由图6知位移延性系数与轴压比成反比.因此将弯曲破坏的延性系数表示为

Δ_u=μ_ΔΔ_y(14)

μ_Δ=((a+bλ_υ))/((c+dn_t))(15)

式中:λ_υ为配箍特征值; a、b、c和d为由实验结果确定的参数.

利用表2的实验数据对式(14)进行拟合分析,得到a=1.012、b=4.194、c=1、d=-0.819,则弯曲破坏的位移延性系数计算式为

μ_Δ=((1.012+4.194λ_υ))/((1-0.819n_t))(16)图 10是本文公式计算值与试验值的比较,由图可见,两者的吻合较好.

图9 弯曲破坏位移延性系数与配箍特征值关系
Fig.9 Relationship between the ductility factor of flexural failure and the stirrup characteristic value

图 10 弯曲破坏位移延性系数计算值与试验值对比
Fig.10 Comparison of calculated and tested displacement ductility