4.1 地震易损性分析及结构的CMR
将表2所示44条地震记录的峰值加速度均放大1.418倍和1.724倍,使该组地震记录的中值PGA分别与罕遇地震(RE)和特大地震(HE)对应的PGA相等(44条地震记录的中值PGA为0.367 g,罕遇地震和特大地震对应的加速度峰值分别为510 cm/s2和620 cm/s2)[7],得到各算例在罕遇地震和特大地震下的中值谱加速度(见表3),采用文献[10-12]建议的倒塌判断标准“地震作用下结构层间侧移角达3%时认为结构达到倒塌极限状态”和文献[13]建立的非线性分析模型,对所有记录采用统一的调整系数,按增量动力分析方法获得结构倒塌概率曲线.取结构有一半地震记录下发生倒塌时44条地震记录的中值Sa(T1)作为SCP,得到各算例的易损性曲线(未进行拟合)见图3～图6.在图3～图6中,RE表示罕遇地震水准,HE表示特大地震水准,CP表示结构的中值倒塌水准,CMRRE表示结构在罕遇地震下的倒塌富裕度,CMRHE表示结构在特大地震下的倒塌富裕度.
表3 RE和HE下的中值谱加速度(单位:g)
Tab.3 Median Sa(T1) for all models under RE and HE/g
根据上述以Sa(T1)描述的结构易损性分析结果,得到各算例的中值倒塌强度SCP以及在罕遇地震和特大地震下的倒塌富裕度和倒塌概率见表4所示.
图3 8层结构的易损性分析结果
Fig.3 Fragility analysis of 8-storey model
图4 12层结构的易损性分析结果
Fig.4 Fragility analysis of 12-storey model
图5 16层结构的易损性分析结果
Fig.5 Fragility analysis of 16-storey model
图6 20层结构的易损性分析结果
Fig.6 Fragility analysis of 20-storey model
表4 RE和HE下的倒塌富裕度和倒塌概率
Tab.4 CMR and collapse probability under RE and HE
从表4可知,所有算例在罕遇地震下的CMR均大于2.0,特大地震下的CMR均在1.7以上; 除了8层算例在特大地震下的倒塌概率为2/44外,所有算例在罕遇地震和特大地震水准下的倒塌概率均为0; 说明按文献[5]建议的结构影响系数设计的Y形偏心支撑钢框架结构有较高的抗倒塌安全储备.从表4又可看出,随结构总层数的增大CMR有上升的趋势,表明层数多的结构比层数低的结构有高的CMR(低的倒塌风险).
4.2 倒塌概率曲线
根据上述结构易损性分析结果,得到4个算例在罕遇地震和特大地震下以CMR为变量的倒塌概率曲线见图7和图8所示.
图7 各算例在罕遇地震下的倒塌概率曲线
Fig.7 Collapse probability of all models under RE
图8 各算例在特大地震下的倒塌概率曲线
Fig.8 Collapse probability of all models under HE
从图7和图8看出,不管是在罕遇地震水准下还是在特大地震水准下,层数越低,结构的倒塌概率曲线越陡,而且在任意给定的倒塌概率下,层数低的结构对应的抗倒塌富裕度均要小于层数高的结构,说明按整条曲线得到的结构抗倒塌富裕度随层数变化的规律与由表4以50%倒塌概率确定的CMR展现的规律非常一致,即公式(1)中结构的倒塌强度SCP 不论按平均值还是中值确定,或者取任意的倒塌概率对应的强度值确定,以Sa(T1)定义的强度指标得到的结构倒塌富裕度规律:“层数多的结构比层数低的结构有高的CMR”具有一定的普遍适用性.
4.3 谱形状因子SSF及结构的ACMR
(1)谱形状因子SSF
根据IDA分析获得的易损性曲线求出的倒塌富裕度CMR,没有反映地震灾害的随机性特征,地震记录频谱特性的影响可通过谱形状因子SSF反映, 谱形状因子SSF可描述为结构的自振周期T和延性能力μc的函数[14-16],为
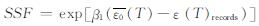(2)
式中:ε(T),records为表3所选44条远震记录对应的谱形状特征值,与结构自振周期有关:当T小于0.5时,可取为0.6; 当T大于1.5时可取为0; 当T在0～1.5之间时,取ε(T)records=0.6×(1.5-T).
ε-0为倒塌分析的谱形状期望值,与场地类别和地震水准有关,当以10%的倒塌概率为可接受倒塌标准时,可取ε-0=1.45.
β1为地震记录频谱特征对结构倒塌能力的影响程度系数,可根据结构的极限延性能力μc由式(3)确定:
β1=0.17×(μ*c-1)0.33(3)
式中:当μc≤8时,取μ*c=μc; 当μc>8时,取μ*c=8.μc由式(4)确定:
μc=Δu/Δy(4)
式中:Δμ为结构极限位移; Δy为结构的有效屈服位移.
需要说明的是,按式(4)度量的结构弹塑性变形能力是用结构有效屈服位移标准化后的变形值,这种标准化使得每个模型初始刚度的确定显得十分重要.初始刚度估计过大,会导致β1值偏大.为了与ATC-63[6]规定的β1计算公式(3)相一致,本文对Y形偏心支撑钢框架结构的有效初始刚度由坐标原点与0.4Vmax确定的割线刚度定义.下面以8层算例为例,对谱形状因子SSF的计算过程简述如下:
(1)由模态分析得到8层算例的T1=1.289 5 s,求出结构的ε(T)records=0.6×(1.5-T)=0.121;
(2)对结构进行Pushover分析(侧向力按倒三角布置),以最大层间侧移达3%作为结构到达极限状态的判定标准,得到结构的极限位移Δu=566.11 mm,按文献[6]建议的有效屈服位移确定方法得到结构的Δy=180.29 mm(见图9所示),由公式(4)得到结构的延性能力μc=3.14;
(3)将μc代入公式(3),求出表1所示44条地震记录的频谱特性对8层算例的影响程度系数β1=0.218 5;
(4)取谱形状期望值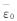
=1.45,将ε(T),records和β1代入公式(2),求出8层算例的谱形状因子SSF为1.337.
按上述方法求出所有算例的SSF见表5所示.
图9 8层算例的 Pushover曲线
Fig.9 Pushover curve of 8-storey model
(2)调整后的倒塌富裕度ACMR
结构调整后的倒塌富裕度记为ACMR可由公式(5)确定:
ACMR=C3D×SSF×CMR(5)
公式(5)中,ACMR为调整后的结构倒塌富裕度; C3D为模型调整系数,空间模型取1.2,平面模型取1.0; 本文Y形偏心支撑钢框架的分析模型均采用平面模型,各算例的模型系数可取为1.0.按公式(5)求出各算例调整后的倒塌富裕度ACMR见表5所示:
表5 各算例的ACMR
Tab.5 ACMR of all models under RE and HE
表5表明,在罕遇地震下和特大地震下Y形偏心支撑钢框架调整后的倒塌富裕度ACMR随结构总层数的增加亦呈上升趋势,在罕遇地震下的ACMR平均值为3.478,在特大地震下的ACMR平均值为2.873,说明按R=3.4设计的Y形偏心支撑钢框架在罕遇地震和特大地震下均有较高的抗倒塌安全储备.
4.4 不确定系数βTOT及ACMR容许值
调整后的ACMR没有反映结构自身的离散性以及各种不确定性的影响,文献[6]在确定结构调整后的倒塌富裕度容许值时对各种不确定性的影响通过一个综合影响系数βTOT进行考虑.βTOT可由地震记录的不确定性系数βRTR,与设计要求有关的不确定性系数βDR,与试验数据有关的不确定性系数βTD以及非线性模型的不确定性系数βMDL综合确定.ATC-63对“结构设计质量”、“结构及结构构件试验数据质量”和“非线性分析模型质量”分为4个等级(优秀、良好、一般、很差),给出了用表2所示44条远场地震记录评估结构抗倒塌性能的βTOT建议值.
对本文设计的4个Y形偏心支撑抗倒塌分析算例在倒三角分布荷载模式下进行Pushover分析,得到各算例在层间侧移角达1/50时的塑性铰分布见图 10,由图 10可知,所有算例在层间侧移角达1/50时,耗能梁段和绝大多数框架梁均不同程度地进入了塑性, 8层和12层结构的柱子仅在底部局部几层位置出现部分塑性(塑性铰转角在0.02以内),20层算例的柱子仅在底层中柱柱脚位置出现塑性铰,而16层算例所有柱子依然在弹性范围内,所有算例在倒塌前能够确保耗能梁段发生剪切屈服,在结构中支撑斜杆不发生破坏的前提下,周边框架梁柱均能够形成“强柱弱梁”的破坏模式.说明本文设计的4个算例符合结构抗震设防要求,体现了“能力设计”思路,框架梁柱均能够形成“强柱弱梁”的延性破坏模式,因此这些算例的“结构设计质量”均属于良好以上水平.
虽然许多学者基于静力试验对偏心支撑钢框架的抗震性能进行了大量研究[17],但由于试验费用较大,许多试验都采用缩尺模型,与实际情况有一定的差距,因此,对各算例的“结构及结构构件试验数据质量”按良好水平[6].
根据文献[6]按“结构设计质量”和“结构及结构构件试验数据质量”均属良好水平给出表2所示44条远场地震波下,对应于不同“非线性分析模型质量”的βTOT见表6.
FEMA695[6]采用“当倒塌强度由中值SCP以对数值给出时,对应的对数标准差和结构综合倒塌不确定因子βTOT相等”的假定,针对不同的综合倒塌不确定系数βTOT,分析给出了可接受的倒塌概率分别为5%～25%的ACMR容许值见表6.表6中ACMR容许值的表示方法如下:如果给定的可接受倒塌概率为10%,则相应的ACMR容许值记为ACMR10%.
图 10 各算例层间侧移为达1/50时的塑性铰分布
Fig.10 Plastic hinges of all models for the storey drifts of 1/50
表6 各算例的βTOT和ACMR允许值
Tab.6 βTOT and acceptable ACMR of all models
由表6可知,可接受的倒塌概率越小,不确定水平βTOT越高,结构需要具备的调整后的抗倒塌富裕度ACMR越大.
本文IDA分析采用的有限元模型,与试验数据之间存在一定的差异[7],且结构倒塌分析没有充分考虑节点变形(加劲板断裂、扭曲,腹板断裂、扭曲),支撑局部加劲板与主体结构的连接构造,以及动应变速率较高时材料变脆等因素对结构破坏模式的影响.偏于保守考虑,本文对各算例的“非线性分析模型的质量”均按很差考虑,即取βTOT=0.85对应的ACMR容许值分析结构影响系数R的可接受程度,评估结构的抗倒塌能力.
4.5 基于罕遇地震CMR的结构抗倒塌性能评估
参考美国FEMA695给出结构性能评估的评判标准:把结构在罕遇地震下的可接受倒塌概率定为10%,考虑到某些个别算例的倒塌概率会超过这个值,取10%的倒塌概率作为倒塌富裕度平均值的可接受标准,取20%的倒塌概率作为倒塌富裕度包络值的可接受标准.即如果设计算例在罕遇地震下的ACMR满足下面两个标准,则认为结构的抗倒塌性能满足要求或结构设计采用的结构影响系数R是可以接受的:
(1)调整后的倒塌富裕度平均值满足公式(6)要求:
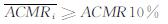(6)
(2)每个调整后的倒塌富裕度满足公式(7)要求:
ACMRi≥ACMR20%(7)
由表5和表6可知:
(1)在罕遇地震下各算例的ACMR平均值为3.477 5,βTOT=0.85对应的ACMR10%为2.97,满足公式(6)要求.
(2)各算例在罕遇地震下的ACMR最小值为2.82,βTOT=0.85对应的ACMR20%值为2.05,满足公式(7)要求;
(3)在罕遇地震下,4个算例的ACMR均介于ACMR5%～ACMR10%之间,说明所有算例在罕遇地震下的倒塌概率在5%～10%之间.
(4)在特大地震下,12层、16层和20层算例的ACMR介于ACMR10%～ACMR15%之间, 8层算例的ACMR介于ACMR15%～ACMR20%之间,说明除了8层以外,所有算例在特大地震下的倒塌概率均不超过15%.至于8层算例得到的ACMR较小的原因,除了我国《建筑抗震设计规范》对层数较少的结构采取的抗震措施相对宽松以外,主要是因为层数低的结构冗余度比层数高的结构具备的冗余度要小所致.
综合以上分析,按R=3.4设计的Y形偏心支撑钢框架在罕遇地震下的倒塌概率不超过10%(在5%～10%之间),结构的安全储备能够满足要求,该文献建议的结构影响系数R值是可以接受的.
需要说明的是,本文评估的结构高度仅为20层以内,因为倒塌评估选择的地震记录仅适用于自振周期在4 s范围内的结构[6].尽管如此,但表5表明一个趋势“结构层数增大,结构倒塌安全储备也增大”,这与美国ATC-63中混凝土结构抗倒塌能力评估结果一致,说明对Y形偏心支撑钢框架取R=3.4对层数超过20层的结构也能适用.
