K-MEANS算法是当前应用最广的一种基于划分的聚类方法,由于理论简单、计算效率高等优势被大量应用于数据挖掘和模式识别等领域^[9].本文采用K-MEANS算法对建筑气候数据进行聚类,根据数据之间的相似程度将其划分为不同子类,对每个子类分别进行清洗,K-MEANS算法步骤可以总结为^[10]:

Step 1:设置聚类个数K,并从数据集{x_l}^N_l=1中随机选取K个样本作为初始聚类中心u₁,u₂,…,u_K;

Step 2:计算数据集中剩余样本与每个聚类中心的欧式距离,并将其划分至距离最近的类别中,欧式距离的定义如式(1)所示;

Step 3:根据式(2)计算得到新的K个聚类中心,其中n_k为第k个子类中的样本数;

Step 4:按K个新聚类中心对样本集进行重新划分,若连续两次得到的划分结果一致,则算法收敛,否则重复Step 2～ Step 3.

K-MEANS算法聚类个数和初始聚类中心的选取对最终聚类结果影响较大,如果选取不当,会导致算法迭代复杂度增加,聚类性能下降等问题.PCA是一种经典的数据分析方法,通过对隐含在数据中的相关性进行分析,按相关性大小将数据划分为不同的簇,将每个簇内的信息合并成一个主分量的同时保证不同簇之间的信息尽量不相关,即PCA能够自动从数据提取K个主分量,这K个主分量相互正交并且包含了数据中的绝大部分有用信息^[11].

对于给定数据集{x_l}^N_l=1,其协方差矩阵可以表示为

对其进行特征值分解可以得到

其中:R_s和R_n分别为信号协方差和噪声协方差矩阵; s_k为信号对应的主分量; s_p为噪声对应的次分量; λ_k为特征值且λ₁≥λ₂≥…≥λ_K>λ_K+1≈λ_K+2≈…λ_M.PCA通常选择占总能量90%的特征值个数为主分量个数K,即

本文将PCA得到的主分量个数K作为K-MEANS算法聚类个数,同时将K个主分量s_k作为K-MEANS的初始聚类中心.

典型的BP神经网络模型由输入层,隐含层和输出层构成,相邻两层神经元节点之间通过权值实现全连接,同一层内部的神经元节点之间不连接.网络的学习过程包含由输入层通过权值映射到隐含层并产生网络输出值的正向传播过程,以及输出层误差由隐含层向输入层映射的反向传播过程.通过正向传播和反向传播相对迭代的学习过程,不断对网络权值进行优化,使输出值最终逼近于预期值^[12].

对于具有n个输入神经元的BP神经网络模型,设第i个输入样本为x_i,i=1,…,n,则由输入层到隐含层的映射关系可以表示为

其中:w_ij为输入神经元和隐层神经元之间的连接权值; θ为阈值; f(·)为Sigmoid激活函数.

由隐含层到输出层的传播过程可以表示为

其中:ω_jk,j=1,…,l,k=1,…; m为隐层神经元与输出神经元之间的连接权值.假设网络预期输出值为y^*_k,则其与输出值之间的误差可以表示为

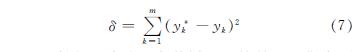
BP神经网络的反向传播过程就是利用梯度下降法按照δ减小的方向对权值{w_ij,ω_jk}和阈值θ进行优化的过程.

由于BP神经网络采用梯度下降法求解,因此权值和阈值初值的选取会对结果产生较大影响,初值选取不当会导致算法收敛于局部最优值^[13],因此需要一种全局优化算法对BP神经网络权值和阀值的初值进行优化,以保证模型最终能够收敛于全局最优解.

本文将遗传模拟退火(Genetic Simulated Annealing,GSA)算法与BP神经网络结合,利用GSA的全局寻优能力优化BP神经网络.GSA算法包含遗传算法(Genetic-Algorithm,GA)^[14]和模拟退火(Simulated-Annealing,SA)^[15]算法2部分内容,综合了GA全局搜索能力强和SA局部搜索能力强的特点.GSA算法首先利用GA在全参数空间内对BP网络权值和阀值进行寻优,得到当前状态下的最优解后,将其作为SA的初值,利用SA在初值附近进行局部搜索,获得满足Metropolis要求的新解,再将该新解作为下一轮迭代中GA的初始种群,通过多次全局搜索和局部搜索的交替迭代,最终获得全局最优解,并将其作为BP网络的初值.所提GAS对BP神经网络进行优化的步骤如表1所示:

表1 GSA算法步骤
Tab.1 Steps of GSA

根据图1所示流程,首先利用PCA对训练数据集进行分析得到大特征值个数K,图2给出了计算得到的归一化特征值谱图,可以看出前4个特征值要远远大于剩余5个特征值,根据式(4)可以计算得到K=4.进而利用 K-MEANS算法对训练数据进行聚类得到的聚类结果如图3所示,由于聚类结果的高维分布(9维空间)情况难以直观观测,图3给出了将9维空间投影到温度和湿度,温度和气压,气压和湿度3种二维平面中,可以看出所提方法能够根据数据之间的相似程度对其进行合理分配,投影到二维平面后仍具有较好的聚类效果,能够自动将相似程度高的数据聚集为同1个子集中,子集内的数据聚集性较好,不同子集间区别性较为明显.

图2 PCA归一化特征值谱
Fig.2 Normalized eigenvalue spectrum of PCA

图3 高维特征聚类结果投影到二维平面
Fig.3 Projection of high-dimensional feature clustering results to a two-dimensional plane

在完成聚类后,根据图1所示流程对4个子类数据分别构建如图4所示BP神经网络模型,输入层节点数为9个气候数据指标,隐层节点数根据文献^[8]所提方法设置为5,输出层节点数可以设置1,即对每个气候指标分别清洗,也可以设置为多个,即对多个气候指标一起完成清洗,但会增加运算时间,并且精度出现一定程度下降,因此本文设置输出节点为1,对每个指标分别进行清洗,即本文所用网络结构为9-5-1.试验中GSA算法的初始种群设置为BP网络初始参数集合C=[ω,w,θ],试验中设置参数空间上下限分别为C_max=[100,100,10]和C_min=[0.1,0.1,0.01],利用GSA算法最终得到的最优参数完成BP神经网络的训练.

图4 BP神经网络结构
Fig.4 Structure of BP

图5中虚线给出了随机选取初值构建BP神经网络在算法迭代过程中反馈误差随迭代次数变化曲线,实线为将GSA获得的最优初值赋予BP神经网络进行迭代时反馈误差随迭代次数的变化曲线,可以看出,GSA-BP模型收敛时的反馈误差更小,收敛速度更快.图5所示结果验证了算法改进的有效性.

图5 不同初值选取方法反馈误差变化曲线
Fig.5 Feedback error variation curve of different initial value selection methods

图6(a)～(i)分别给出了针对测试数据气压,温度,湿度,风向,风速,总云量,地表辐射强度,直接辐射强度,红外辐射强度9个维度进行清洗得到的结果与真实值之间的残差变化曲线,为了对比,图6中给出了采用文献^[8]所示方法在相同条件下对测试数据进行清洗得到的结果.从图6可以看出,对于上述9个维度的数据清洗结果,所提方法相对于文献^[8]方法的网络输出值与真实值较为接近,残差较小,表明所提方法数据清洗性能更优.同时温度,湿度和总云量3个维度预测结果出现了少数误差较大点,对其进行分析可知其与左右两侧值之间的差距较大,且明显与实际气候情况不符,采用所提方法修正后数据曲线更加平滑,与实际情况接近.表2给出了所提方法和文献[8]方法数据清洗结果的均方误差和有效清洗效率指标,可以看出,对于本文所用试验数据,所提方法可以获得更高的清洗效率和更小的均方误差,即数据清洗性能更优.

图6 9维数据清洗误差变化曲线
Fig.6 9 dimensional data cleaning error change curve

表2 两种方法对测试集的清洗结果
Tab.2 The cleaning results of the two methods on the test set

在实际工程应用中,受限于训练数据集的获取手段匮乏,有时难以获得足够的训练数据以保证模型得到充足的学习,因此小样本情况下的数据清洗能力也是评估一种方法性能的重要考量指标.在本节内容中,我们分别将训练数据容量减少为总量的20%,40%,60%和80%,分别对所提方法和文献[8]方法的数据清洗性能进行评估,图7给出了2种方法的有效清洗率随着训练样本数的变化曲线,可以看出,随着训练样本数的减少,2种方法的数据清洗性能都出现了不同程度的下降,但是所提方法的性能均优于文献[8]方法,在训练样本数减少至40%时,所提方法仍能获得优于90%的有效清洗率.

图7 有效清洗率随训练样本数变化曲线
Fig.7 The effective cleaning rate varies with the number of training samples

在实际工程实践中,数据清洗模型对不同测试数据的泛化能力是评估算法性能的一项重要指标.如果一种数据清洗模型在完成训练后,对不同的测试数据均能取得较好的清洗效果,则认为该模型具有较强的泛化能力.

在前述试验的基础上,采取每次从国家气象局网站随机读取该城市2000年～2008年真实年14时的气候数据构建测试数据集的方式对所提方法的数据清洗性能进行验证,每组测试数据集包含256组数据,重复进行10次随机抽取试验,并对结果求平均.表3给出了所提方法和文献[8]方法数据清洗结果的均方误差和有效清洗效率指标,可以看出在测试数据集发生变化时,所提方法的性能依然优于文献[8]方法.同时将结果与表2进行对比可知,在面对不同测试集时,所提方法的数据清洗性能与单一数据集的数据清洗性能非常接近,验证了所提方法的泛化能力.

表3 两种方法对不同测试集的清洗结果
Tab.3 The cleaning results of the two methods on different test