(1.清华大学 土木工程系,北京100084; 2.国质(北京)建设工程检测鉴定中心,北京100837)
(1.Department of Civil Engineering,Tsinghua University,Beijing 100084,China; 2.State Quality(Beijing)Construction Engineering Testing and Appraisal Center,Beijing 100837,China)
DOI: 10.15986/j.1006-7930.2021.03.001
随着城市建筑高度的增加和复杂程度的增加,构件尺寸也逐渐增大,大尺度钢筋混凝土构件被广泛应用.研究表明,随着试件尺寸的增加,混凝土构件的强度试验值存在有规律下降的现象.1956年Neville[1]对抗压强度在13～48 MPa范围内的不同尺寸混凝土立方体试件进行试验,结果表明小尺寸试件抗压强度较高; 1976年Malhotra[2]通过研究抗压强度在7～48 MPa范围内的不同尺寸混凝土圆柱体试件抗压试验,发现大尺寸试件抗压强度较低.Cotterell等[3]和Ince等[4]对不同尺寸混凝土立方体试件做了大量的试验研究,得出同样的结果.1967年Kani[5-6]通过不同尺寸简支梁的试验,发现随着梁截面高度的增加,无腹筋梁破坏时的抗剪强度与尺寸有关,当其他条件相同时,仅截面有效高度从200 mm增至800 mm,截面平均剪切应力降低约40%; Shin[7]、Angelakos[8]和Base[9]用统计及试验的方法进行分析,认为混凝土梁抗剪强度与尺寸有关; 1999年Tan[10]通过对大尺寸混凝土深梁的研究,认为梁的开裂强度与尺寸无关,但极限抗剪强度与尺寸有关; 1981年Chana[11]通过36根混凝土简支梁的试验,进一步证实了混凝土梁的抗剪强度与尺寸有关; 2001年Collins[12-13]研究发现少量箍筋的大尺寸钢筋混凝土构件抗剪强度与尺寸有关,并且修正了美国ACI318规范的抗剪强度设计值; 2004年Sene[14]进行了3组不同尺寸正方形截面柱的轴心加载试验,研究表明随着构件尺寸的增加,柱破坏时最大压应力值减小; 2004年Nemecek[15]对不同尺寸的钢筋混凝土柱进行了偏压试验和数值模拟,结果表明大尺寸柱峰值后强度下降要比较小尺寸柱降低更快; 1987年Abrams[16]进行了18个不同尺寸钢筋混凝土梁柱节点的试验,研究结果表明小尺寸节点的钢筋粘结破坏更严重.1991年Bazant等[17-19]通过对不同尺寸混凝土试件进行研究,认为混凝土的力学行为和尺度有关.2001年Brocca[20]基于微平面模型,用有限元方法模拟了Bazant的试验,研究发现大尺度试件峰值荷载计算值较试验实测值稍小; 2012年Li等[21]的研究表明,以剪切破坏为主的钢筋混凝土梁柱节点的抗震性能与尺寸有关.
钢筋混凝土构件受剪开裂后,混凝土单元实际上处于拉压双向应力状态.混凝土的抗压强度及其所对应的压应变均较单轴受压时有所降低,这种现象一般称为混凝土的软化.1961年Robinson[22]在钢筋混凝土梁的腹板压碎试验中首次发现了混凝土的软化现象.1972年Robinson等[23]进行了钢筋混凝土平板的双向受剪试验,发现钢筋混凝土受剪单元实际上处于拉压双向应力状态,混凝土构件开裂后,某一方向的抗压强度将会由于垂直于该方向拉应力的存在而出现软化,使混凝土的峰值应力有所降低.1981年Vecchio等[24]通过钢筋混凝土平板试验,首次提出用软化系数来描绘混凝土的软化特性,并将其定义为混凝土软化峰值压应力与单轴圆柱体抗压强度的比值.Takehisa[25]、Izumo[26]、Shirai[27]、Mikame[28]等也相继证明了主拉应变对混凝土软化系数有很大的影响,提出了软化系数的计算方法.1991年Hsu等[29-30]改进了试验设备,对35块尺寸为140 cm×140 cm×18 cm的大型钢筋混凝土平板进行了试验,建议软化系数仅表达为主拉应变的函数.1998年Zhang等[31]研究了混凝土抗压强度f'c等因素对软化系数的影响,提出软化系数与主拉应变有关.
目前对钢筋混凝土梁柱节点的抗剪强度研究还主要是依据小尺度构件的试验研究,相关的抗剪机理研究和抗剪承载力计算方法均是在小尺度试验构件的基础上建立的.限于试验条件,对于大尺度梁柱节点的力学性能和破坏机理的研究还很不充分,节点截面尺寸对大尺度钢筋混凝土梁柱节点抗剪承载力的影响尚无详尽研究.本文结合试验研究,对节点的抗剪机理进行研究,考虑节点尺寸对混凝土软化效应的影响,对大尺度钢筋混凝土梁柱节点的抗剪承载力计算方法提出了修正建议.
1978年Paulay等[32～34]对钢筋混凝土梁柱节点进行研究,提出了斜压杆-桁架理论.
图1 节点外部作用
Fig.1 External actions of interior joint
图2 节点核芯区斜压杆-桁架抗剪机制
Fig.2 The strut-truss shear mechanism of the joint core
节点区域受力复杂,在节点附近梁柱传递的弯矩、剪力等外部作用下,节点核芯区内分别形成水平剪力Vjh和竖向剪力Vjv(图1).
Vjh=Cc1+Cs1+T2-V4=Cc2+Cs2+T1-V3 (1)
一方面,梁、柱端受压区混凝土传给节点边缘的压力有相当一部分在节点内合成为对角线方向的斜向压力Dc,由核芯区混凝土承担,形成斜压杆机制; 另一方面,贯穿节点的梁筋、柱筋和混凝土之间分别产生的粘结效应以周边剪力流的形式传入节点,在节点内形成斜向压力Ds,由节点内的箍筋和柱纵筋承担,形成桁架机制(图2); 分析了节点水平剪力Vjh的组成,给出了相应的计算方法.
Vjh=Vch+Vsh (2)
Vch=Dccosα (3)
Vsh=Dscosα (4)
式中,Cc1、Cc2分别为节点附近下侧、上侧梁端受压区混凝土形成的压力; Cs1、Cs2分别为节点附近下侧、上侧梁端纵筋受压形成的压力; T1、T2分别为节点附近下侧、上侧梁端纵筋受拉形成的拉力,其中T1=As1fs1、T2=As2fs2,As1、As2分别为节点附近下侧、上侧梁端纵筋的面积,fs1、fs2分别为节点附近下侧、上侧梁端纵筋的应力; 其中由贯穿节点的下侧、上侧梁纵筋经粘结效应形成的传入节点的剪力可分别表示为(Cs1+T1)、(Cs2+T2); V4、V3分别为节点附近下侧、上侧柱端的水平剪力; Vch、Vsh分别为节点内由混凝土和钢筋机制承担的水平剪力.
2012年Choi[35]等在Paulay斜压杆-桁架机理的基础上,考虑混凝土的软化效应,依据斜压杆机制和桁架机制对节点抗剪强度进行定量分析,认为在斜压杆方向的混凝土斜向压应力达到混凝土极限抗压强度时节点发生剪切破坏,建立了节点抗剪承载力计算式(5).
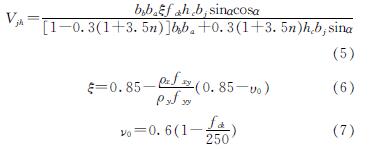
式中,ba为斜压杆宽度,α为斜压杆倾角,ξ为欧洲规范Euro Code-2[36]中规定的混凝土软化系数,fxy和fyy分别为节点水平方向钢筋(梁筋和箍筋)和竖直方向钢筋(柱筋)的屈服强度,ρx和ρy分别为节点水平方向和竖直方向钢筋的配筋率,fck为混凝土抗压强度标准值,MPa.
1999年Hwang[37-39]等建立了钢筋混凝土梁柱节点软化拉-压杆模型,认为节点内水平箍筋和中间柱筋形成拉杆、混凝土形成压杆,共同组成拉压杆机构抵抗节点剪力.如图3所示,图中D为斜压杆压力,Fh为水平拉杆拉力,Fv为竖向拉杆拉力.
图3 软化拉-压杆模型
Fig.3 Softened strut - tie model
当斜压杆方向的混凝土压应力达到极限抗压强度时节点发生剪切破坏,并考虑混凝土的软化效应,建立节点抗剪承载力计算式(8).
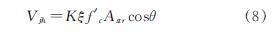
式中: K为拉压杆系数,θ为主斜压杆倾角,Astr为斜压杆横截面面积.f'c为混凝土圆柱体抗压强度,MPa; 根据欧洲CEB-FIP规范[40],混凝土圆柱体抗压强度和混凝土立方体抗压强度标准值之间的换算关系为f'c=0.80fcu,k.
根据Hsu[30-31]、Vecchio[41]等对混凝土软化效应的研究成果,Hwang[39]通过试验研究,认为节点剪切破坏时,核心区平均主压应变εd可降低至-0.001,此时经过裂缝的水平和竖向钢筋均屈服,核心区水平平均拉应变εt和竖向平均拉应变εl均可达到0.002,则根据应变协调条件(εt+εl=εd+εr),可得到节点核心区平均主拉应变εr约为0.005(0.002+0.002+0.001),由式(9)可得到软化系数ξ的简化计算式(10).
2004年Attaalla[42]提出了一种钢筋混凝土梁柱节点的抗剪通用模型.该模型采用平均应力和平均应变的假设,认为节点核心区的平均主压应力达到混凝土极限抗压强度时发生剪切破坏,考虑混凝土的软化效应,在受力平衡和变形协调的基础上建立节点极限剪应力的计算式(11),并给出了软化系数ξ的设计经验计算式(10).
图4 节点核芯区单元体受力平衡
Fig.4 Stress balance of element in core area of joint
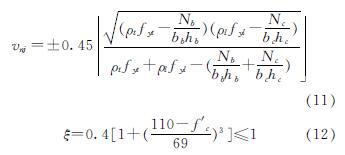
式中,vnj为节点水平方向的极限剪应力,MPa; fyt和fyl分别为节点水平方向钢筋和竖直方向钢筋的屈服强度,ρt和ρl分别为节点水平方向和竖直方向钢筋的配筋率; Nb和Nc分别为梁和柱内的轴力; η为几何系数,中节点取1.0.
1982年Jirsa等[43]依据300多个RC梁柱边柱节点和中柱节点试验结果的分析,指出梁柱节点初裂到破坏期间的剪力均由混凝土斜压杆(虚线范围内两头小中间大的混凝土“瓶型斜压杆”)承担,箍筋的作用主要是对斜压杆混凝土的约束(图5).
图5 节点核芯区斜压杆抗剪机制
Fig.5 The strut shear mechanism of the joint core
斜压杆机理力学模型原理明确,被美国ACI318[44]规范和日本AIJ[45]规范采用.该方法认为节点剪力主要由混凝土斜压杆承担,节点箍筋按构造配置即可,因此使美国ACI318规范和日本AIJ规范所计算的节点配箍量较小.
美国规范ACI318[44]在节点设计中未考虑轴压比的影响,认为梁柱节点中箍筋的作用在于约束混凝土,忽略了桁架模型的作用,从而基于混凝土斜压杆模型建立了与混凝土抗压强度相关的梁柱节点抗剪承载力计算式(13).
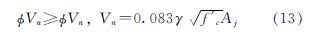
式中,Vu为节点水平极限剪力; φVu为节点的设计剪切强度; φ为强度降低系数,取值0.85; Vn为节点的名义剪切强度; f'c为混凝土圆柱体抗压强度,MPa; 对于普通混凝土结构的抗震节点,γ为梁柱节点类型影响系数; Aj为节点区有效横截面面积Aj=bjhj,bj为节点有效宽度,hj为节点横截面高度.
中国规范GB50010[46]所用的抗震节点设计方法是以20世纪70年代末完成的系列试验结果为依据经专家综合分析提出的式(14).认为框架节点的抗剪承载力由混凝土斜压杆和水平箍筋两部分抗剪承载力组成,其中水平箍筋是通过其对混凝土斜压杆的约束效应来增强节点抗剪承载力的.
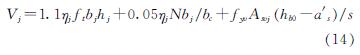
式中,bb为梁截面宽,bc为柱截面宽; hc为柱截面高度(水平剪力方向),hb0为梁截面有效高度,a's为梁纵向受压钢筋合力点至截面近边的距离; N为柱端轴压力,取N≤0.5fcbchc; ft为混凝土轴心抗拉强度,MPa; fc为混凝土轴心抗压强度,MPa; Asvj为箍筋各肢的全部截面积; fyv为箍筋屈服强度.
1987年Abrams[16,47]分别对常规尺寸节点(340 mm)和约1/11～1/3倍常规节点尺寸的小尺度钢筋混凝土梁柱节点进行了试验研究.本次试验主要对常规尺寸节点(300 mm)和约1.5～3倍常规尺寸节点的大尺度钢筋混凝土梁柱节点进行试验研究.上述试验按相似关系设计,混凝土保护层厚度、试件尺寸及配筋均符合相似原则.试验现场照片见图6,试件参数见表1.
图6 试验现场照片
Fig.6 Scene pictures of the field experiments
分别采用前述5种方法得到上述节点试验试件的抗剪承载力计算值Vjc,并与试验值Vjt进行比较,见图7.
可见,这几种方法得到的节点抗剪强度变化趋势相近.对于常规尺寸的节点,传统方法计算的节点抗剪承载力均较为准确; 而对于较小或较大尺度的节点,计算的节点抗剪承载力与试验值偏差较大.随着节点尺寸的增大,无论是在单调荷载还是低周往复荷载作用下,节点抗剪承载力试验值Vjt与计算值Vjc的比值均明显降低,表明采用传统方法计算的大尺度节点抗剪承载力偏大,节点的抗剪承载力被高估了,使大尺度钢筋混凝土梁柱节点的安全性降低,应考虑必要的调整.
表1 不同尺度钢筋混凝土梁柱节点试件参数表
Tab.1 Comparison of shear bearing capacity in reinforced concrete beam-column joints with different scales
图7 不同尺寸节点抗剪承载力
Fig.7 Shear capacity of joints of different sizes
节点核心区的剪切变形γtl与节点尺寸有关,1982年Jirsa等[43]最早提出了节点核心区剪切变形的计算方法,如图8所示.
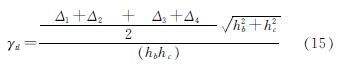
试验采用位移计实测节点核心区对角线方向的变形Δ(见图8),按式(15)可得到节点剪切变形γtl.
试验得到了不同尺度节点试件达到极限状态时的节点剪切变形.试验表明:节点剪切变形受节点尺寸影响较大,节点剪切变形并不是随着节点尺寸的增大而增大,无论是单调加载还是低周往复加载,随着节点尺寸的增大,节点达到极限状态时,节点剪切变形逐渐减小(见图9).
图8 节点核心区变形
Fig.8 Deformation of joint core
图9 节点发生剪切破坏时的剪切变形
Fig.9 Shear deformation of joints during shear failure
Paulay等[50]认为,节点混凝土主拉应变方向应与开裂方向垂直.Attaalla[48]、Cheung[51]等试验研究表明,节点核心区的主拉应变约是主压应变的2～10倍.
为了能够对节点的抗剪强度和剪切变形进行简单、可靠的预估,Attaalla[48-49]提出了如下力学假设,对节点核心区的平均变形和平均应变进行了简化研究:
(1)节点变形很小;
(2)节点是平面节点;
(3)节点在变形期间没有发生平移或旋转;
(4)忽略梁筋和柱筋穿过节点的传力作用;
(5)节点边界假定为固结;
(6)应力和应变按平均值考虑;
(7)节点变形过程中两个对角线之间的角度变化忽略不计.
在上述假设下,认为节点的总变形由节点核心区的膨胀变形和剪切变形两部分组成,如图 10所示.
图 10 节点变形的组成部分
Fig.10 Components of joint deformation
图中,θ为节点斜对角线与水平方向的倾角,cj为节点受压区深度,u和v分别是节点核心区水平和竖向的膨胀变形,us和vs分别是由节点剪切变形而引起的节点水平和竖向变形,γh和γv分别是由节点剪切变形引起的节点水平和竖向的剪切角.
按照Attaalla的方法,由节点核心区的剪切变形γtl,可分别计算节点核心区水平方向的平均应变εt和竖直方向的平均应变εl.
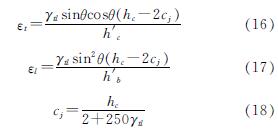
根据应变莫尔圆,可分别计算节点核心区的平均主拉应变εr和平均主压应变εd.
式中,an为节点核心区平均主压应变ε2与水平轴的倾角.
试验得到节点试件在开裂、屈服、极限状态时的节点剪切变形γtl,按照式(16)～(20)计算节点核心区平均主应变,可得到节点核心区的平均主拉应变εr和主压应变εd之间的相互关系(见图 11、图 12).
图 11 单调荷载下节点试件的平均主应变
Fig.11 Mean principal strain in joint specimens under monotonic loads
图 12 往复荷载下节点试件的平均主应变
Fig.12 Mean principal strain in joint specimens under reciprocating loads
由图 11、图 12可见,随着节点剪力的增大,节点核心区的平均主拉应变和主压应变均逐渐增大.节点刚开始开裂时,拉应变较小,混凝土软化现象还不明显,不同尺度之间节点核心区的平均主拉应变εr与主压应变εd相差不大; 随着节点剪力的增大,与主压应变相比,节点核心区混凝土主拉应变的增加程度逐渐增大.但是,与小尺度节点相比,大尺度节点核心区平均主拉应变的增加程度不明显.当节点剪切破坏时,小尺度节点核心区的平均主拉应变约是大尺度节点的2～10倍,表明节点核心区平均主应变受节点尺寸影响较大.
Vecchio[41]、Hsu等[29-30]、Miyahara[25]、Mikame[28]等均认为,混凝土开裂后产生的软化效应与主拉应变有关,并分别给出了开裂混凝土抗压强度软化系数(见表2).
表2 开裂混凝土抗压强度软化系数
Tab.2 Softening coefficient of compressive strength in cracked concrete
由表中软化系数计算式可见,节点混凝土软化与节点核心区主应变有关,节点剪切破坏时,随着节点主拉应变的增大,混凝土软化现象逐渐增强.但是,表中计算式均是相对于常规尺寸的混凝土构件而建立的,从前述试验结果可见,随着节点尺度的增大,节点核心区平均主拉应变的增加程度不明显,如仍选用上述计算式则不能反映主应变对大尺度节点混凝土软化效应的影响.
由试验结果可知,按照前述传统方法,随着节点尺寸的增大,节点的抗剪承载力明显被高估了.分析其原因,未能准确反映大尺度节点混凝土软化效应与节点尺寸之间的关系,对大尺度节点开裂后混凝土的强度退化不能给出全面的描述,必然引起大尺度节点抗剪承载力计算的误差.应调整大尺度节点混凝土软化系数计算式,将软化系数乘以修正系数αh.
基于Bazant[52]名义应力的尺寸效应计算式(21),依据试验结果,拟合大尺度节点混凝土软化系数的修正系数αh.
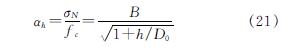
式中,σN为名义应力,B、D0为常数,fc为混凝土抗压强度,h为构件截面高度.最终修正系数如下:
图 13 单调荷载下软化系数与节点尺寸的关系
Fig.13 The relationship of softening coefficient and joint size under monotonic loads
图 14 往复荷载下软化系数与节点尺寸的关系
Fig.14 The relationship of softening coefficient and joint size under reciprocating loads
由图 13、图 14可见,调整后大尺度节点的混凝土软化系数可以较好的反映随节点尺寸对混凝土软化现象的影响,使预测的大尺度节点抗剪承载力的计算值和试验值吻合较好.
分别在单调荷载和低周往复荷载作用下,考虑节点尺寸对混凝土软化效应的影响,调整大尺度钢筋混凝土节点抗剪承载力的计算方法.
对于式(5)、式(8)、式(11)和式(14)的节点抗剪承载力计算式,可采用式(22)和式(23)的修正系数进行调整.由图(15)、图(16)可见,调整后的大尺度节点抗剪承载力计算值与试验值吻合良好.
图 15 单调荷载下节点抗剪承载力的修正
Fig.15 Adjustment of shear capacity under monotonic loads
图 16 往复荷载下节点抗剪承载力的修正
Fig.16 Adjustment of shear capacity under reciprocating loads
(1)试验表明,随着节点尺寸的增大,按传统方法所得的钢筋混凝土梁柱节点抗剪承载力被明显高估了,应考虑节点尺寸对大尺度节点抗剪承载力的影响.
(2)试验表明,与常规尺寸节点相比,随着节点剪力的增大,大尺度节点核心区的剪切变形和平均主拉应变的增加程度越来越不明显.
(3)节点混凝土软化效应与节点核心区主应变有关,但按传统方法所得的节点混凝土软化系数不能准确反映大尺度节点的混凝土软化效应,主要原因在于大尺度节点核心区平均主拉应变的增加程度不明显导致,应对大尺度节点混凝土软化系数进行调整;
(4)节点尺寸对钢筋混凝土梁柱节点抗剪承载力的影响,主要体现在节点尺寸对节点混凝土软化效应的影响,应考虑尺寸影响调整节点抗剪承载力的计算方法,调整后大尺度钢筋混凝土梁柱节点抗剪承载力的计算值和试验结果吻合良好.
钢筋混凝土梁柱节点抗剪承载力的计算非常复杂,既有计算方法均是在一些合理的力学模型假设或大量试验基础上得到.影响节点抗剪承载力的因素很多,节点尺寸仅是主要影响因素之一,但由于试验条件的限制,对于大尺度梁柱节点的试验研究很少.本文仅进行了约1.5～3倍常规尺寸节点的大尺度节点试验,并在大量既有研究的基础上,依据本次试验的结果,研究节点尺寸对大尺度节点混凝土软化系数的影响,对大尺度钢筋混凝土梁柱节点抗剪承载力的计算方法提出了建议,其通用性还有待进一步的试验验证和研究.本文对节点平均应变的研究是在一定力学假设的前提下进行,受梁柱变形的影响,对节点核心区应变的直接量测较为困难,还有待试验技术的进一步提高.
