基金项目:国家自然科学基金资助项目(51908356); 中国博士后科学基金资助项目(2019M662056); 浙江省自然科学基金资助项目(LQ19E080013)
第一作者:冯晓东(1987-),男,博士,副教授,主要从事大跨度结构及智能结构研究.E-mail:xiaodong.feng@csu.edu.cn
(1.绍兴文理学院 土木工程学院,浙江 绍兴 312000; 2.浙江大学 建筑工程学院,浙江 杭州 310000)
(1.College of Civil Engineering,Shaoxing University,Shaoxing 312000,China; 2.College of Architectural Engineering,Zhejiang University,Hangzhou 310000,China)
tensegrity structure; motion of develop; vector mechanics of structures; motion trajectory
DOI: 10.15986/j.1006-7930.2021.03.006
张拉整体结构(Tensegrity)是一种由一系列连续的受拉构件和一系列离散的受压构件组成的稳定的自平衡结构体系[1-2].但在张拉整体概念提出之初,由于未出现有效的分析设计理论与方法,该结构在工程领域的应用较少,而在建筑和艺术领域的应用较多.直到20世纪80年代初,工程界学者们才被这种具有独特魅力的结构体系所吸引,并在航空航天[3]、智能机器人[4]和土木工程[5]等不同学科领域取得了多样化的发展与应用.随着张拉整体结构理论的推广,可展结构领域中也出现了张拉整体结构的身影.蔡建国[6]提出因为张拉整体结构体系拥有大变形、小应变的特点,所以该结构体系在张拉成型的过程中将产生索杆机构运动,并通过预应力获得刚度,非常适合应用于可展结构.Sultan[7]构造了与无穷小机构运动方向相切的路径,并利用鲁棒非线性反馈控制对这些路径进行了精确跟踪,证实了利用无穷小机构原理和非线性运动方程可运用于确定张拉整体结构的展开方式,揭示了通过阻尼、无穷小机构、运动速度和部署时间所耗散的能量和功率之间的联系.彭海军[8]和张亮[9]在张拉整体结构的节点处设置一个轮滑,并推导了压杆和滑轮索的相关公式,建立了研究张拉整体动态特性的综合动力学模型,为研究张拉整体结构的可展性能提供了一种可行的动力学计算方式.
相比于其它传统的可展结构,张拉整体结构这种具有独特魅力的新体系依然年轻,其可展性能依然是近几年来学者们研究的热点.随着学者们的深入研究,针对张拉整体结构可展性能的计算理论日趋成熟与完善,其变形时的驱动原理和展开路径是研究的重要内容之一.肖特[10]构建了一个新颖的圆柱形张拉整体结构,并利用外力对模型进行轴向拉伸和压缩,根据变形过程中索长度的变化趋势从而找到驱动索以实现结构的折叠和展开,论证了该结构在环形天线与空间伸展臂领域的适用性.李冰岩[11]构建了可展开环形张拉整体天线,通过拉索之间长度的协调对结构进行展开和折叠,并对结构进行展开功能试验,验证了可展开环形张拉整体天线展开方案的可行性,通过刚度试验得到了样机在自由模态下的固有频率.罗阿妮[12]在三杆张拉整体结构的基础上提出一种星形张拉整体可展结构,并在结构内部设置一个伸缩杆,通过伸缩杆的驱动实现结构的变形,对其工作过程和结构的折展可行性进行仿真研究和理论认证.刘贺平[13]运用实体模型试验和数值模拟的方法对四杆张拉整体机器人的运动过程进行研究,提出在中部索长度不变的情况下,改变顶部索和底部索的长度就能驱动机器人的变形和移动.
上述工作在研究结构展开的过程中,都采用了索协调变形的方式驱动结构的展开.即结构在进行展开运动的过程中,结构的每一根索都始终参与了计算.受此启发,本文以quadruplex张拉整体结构单胞为基本单元,提出一种新的展开方式:在固定底部节点的情况下,改变顶部索的长度并施加预应力,驱动结构变形.在结构变形的过程中,中部索将从松弛状态转化为拉紧状态,即中部索除拉紧状态以外,其他状态下将不参与结构展开过程中的计算.最后结合商业软件MATLAB和ANSYS研究张拉整体结构基本单元的展开方法,分析结构中构件的运动路径和力学性能,促进张拉整体结构体系在实际工程中进行应用.
基于向量式结构力学的基本理论和张拉整体结构的特点,在建立计算模型时采用以下假定:
①结构构件间的采用铰接的连接方式;
②结构中的构件均为二力杆件,但拉索单元只能承受轴向拉力;
③结构的外力、内力和质量均集中在节点上;
④不考虑自重效应.
根据向量式结构力学理论,每一个结构将被离散为一系列的空间点,并用这一系列有限数目点的位置来描述复杂的结构形式和几何状态,将结构运动变形问题转变为空间点的运动问题[14].此时,结构杆件受到的荷载、内力、约束、质量和运动的条件等都集中在同一个点上,并用力和点的位移来描述,而点的运动则用牛顿第二定律计算.由于张拉整体结构中空间点的自由度只有XYZ三个方向的平移自由度,所以空间点的运动所满足的控制方程如式(1)所示[14].
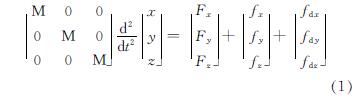
式中:假设结构中的某个空间点为Q,其位置向量为[x y z]T,外力向量为[Fx Fy Fz]T,内力向量为[fx fy fz]T,质量矩阵为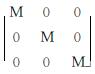 ,其中M可按式(2)[14]计算.
,其中M可按式(2)[14]计算.
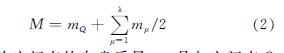
式中:mQ为空间点的自身质量; λ是与空间点Q连接的构件的个数; mμ是每个连接在空间点Q的单元的质量,分配到空间点时通常为两个空间点之间单元质量的一半.[fdx fdy fdzT]是作用于空间点Q的阻尼力向量,该阻尼力在本例中是一个虚拟的阻尼力,目的是为了在该结构展开的过程中避免由荷载产生的振动效应的影响,Q点的阻尼力向量满足式(3)[14].
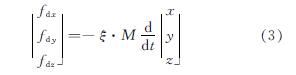
式中,ξ是虚拟的阻尼比.
为避免求解过程中出现复杂的迭代和结果不收敛的问题,根据向量式结构力学的理论,求解式(1)时采用显示积分的方法进行求解[14].因此空间点Q的加速度q¨n为
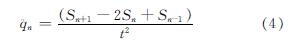
式中:Sn+1、Sn和Sn-1分别时空间点Q在n+1、n和n-1时刻的位置向量; t为计算时间.
将公式(4)和(3)代入式(1),得位移得迭代式(5).
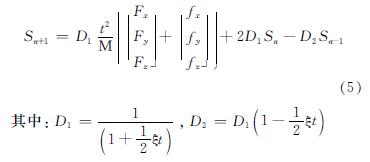
当n=0时,则需要第-1时刻的位移S-1,所以需要中央差分公式[14]在运算起步时进行特殊的处理.设某个空间点的初始位置向量Q0,初始速度向量为(·overQ)0,初始外力向量和初始内力向量为F0和f0,由中央差分公式得以下条件.
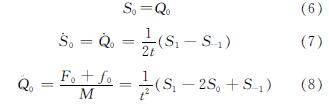
将式(6)代入(8),并联立式(7)和(8),解得S1和S-1:
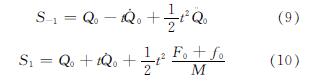
所以,将式(9)和(3)代入方程式(5)得:
当n>0时:
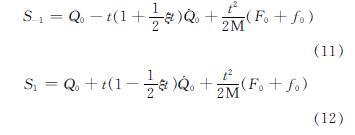
当n>1时,方程式为式(5).
基于向量式结构力学的基本理论[14],当任意方向的力Fr作用于空间点Q时沿着坐标轴方向的等效力分量为
Fx=Fr·ex (13)
Fy=Fr·ey (14)
Fz=Fr·ez (15)
式中,ex、ey和ez为空间点Q域坐标(x,y,z)下的基底向量.
假设杆系构件G的内力由构件长度的变化产生,即只有拉力和压力.假设空间点Q与空间点W之间由杆系构件G连接,则杆系构件G的内力集中在空间点Q为[14]:
fx=fr·ix (16)
fy=fr·iy (17)
fz=fr·iz (18)
式中:ix,iy和iz为杆系构件G的方向向量.假设空间点Q与空间点W的位置向量分别为[Qx Qy Qz]T和[Wx Wy Wz]T,则方向向量公式为[14]:
ix=(|Qx-Wx|)/L (19)
iy=(|Qy-Wy|)/L (20)
iz=(|Qz-Wz|)/L (21)
上式中,L为杆系构件G的长度,由公式(22)表示.
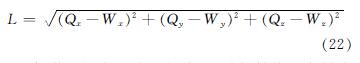
假设空间点Q与空间点W的初始位置向量为[Qx0 Qy0 Qz0]T和[Wx0 Wy0 Wz0]T,则杆系构件G的原长L0为:
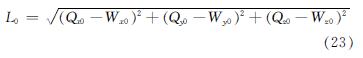
由材料力学的理论[15]可知,杆系构件G的拉力或压力为
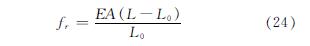
式中,E为弹性模量,A为构件截面面积.当fr为正,则为拉力; 若fr为负,则为压力.
精确的增量时间步长是中央差分计算得以稳定收敛的前提.换而言之,当计算时间步长t小于临界步长t0时,持续计算所得的累积误差才可以维持在容许的范围内,即收敛为一个较为精确的结果.当计算时间步长t小于临界步长t0时,计算结果将不收敛.
然而,构件的运动行为和参数值对临界步长的确定有直接的影响.不同的结构对应不同的临界步长,同一种结构不同的变量方程所要求的临界步长也不同.因此文献[14]中以一个刚性杆件结构为例,推导出了临界步长的估算公式,并应用到该文献柔性结构的算例中.所以,本文的算例参考公式(25)估算临界步长为
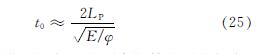
式中:LP为连接空间点Q的所有构件的平均长度,φ为构件的质量密度.
对于本文的驱动方式,在张拉整体结构运动的过程中,被动索往往会受压并退出计算,其限值FB由公式(26)求出.
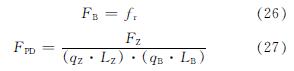
式(26)和(27)中,FB为被动索受到的压力; fr由式(26)计算可得; FPD是被动索是否参与下一时刻计算的判定条件; FZ是主动索连接的两个空间点所受到的力; qZ和qB分别是主动索和被动索力密度的比值; LZ和LB分别是几何稳定下,张拉整体结构中主动索和被动索的长度.在确定结构折叠形态的过程中,当FB<FPD时,被动索继续参与下一时刻的计算; 当FB≥FPD时,被动索不参与下一时刻的计算.
令
FB=FPD (28)
联立方程(26)、(27)和(24)可得当被动索受到的压力FB等于FPD时,被动索的长度LPD由下式表示:
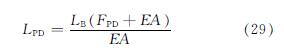
式中:E为杨氏模量; A为截面面积; FB由第一个程序输出.在结构进行展开运动的过程中,当被动所连接的两个空间点上的距离LBD<LPD时,则被动索不进入下一个时刻的计算; 当LBD>LPD时,被动索进入下一个时刻的计算.
假设一个空间网格体系有w根杆件和v个自由度,其自应力模态数为ZS和独立机构位移模态数Dm可分别由以下公式确定[16]:
ZS=w-rA (30)
Dm=dKv-rA (31)
式中:rA是平衡矩阵的秩,dK是结构的空间维数.当ZS=0和Dm>0时,结构将转化为可发生有限位移的机构; 当ZS>0和Dm>0时,结构将变成同时拥有机构位移和自应力模态的张拉整体结构.在分析张拉整体结构时,首先需要考察其自应力模态能否刚化其无穷小机构位移模态,同时最终的自应力模态必须满足压杆受压、拉索受拉的条件,因为拉索只具有单向的受拉刚度,无法承受压力[17].
切线刚度矩阵KT的正定性可判断张拉整体结构的稳定性,其表达式(32)所示[18]:
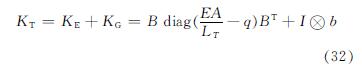
式中:KE是结构的切线刚度; KG是与自应力模态有关的几何刚度矩阵; E为弹性模量; A为构件截面面积; LT为杆件的原长; I∈R3×3为单位矩阵; 为张量积.平衡矩阵B和矩阵β由式(33)和(34)表示[19]:
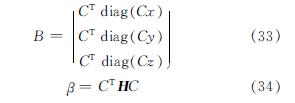
其中:H=diag(q)
式中,H是力密度矩阵; 矩阵q由式(35)和(36)表示:
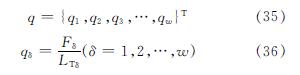
式中:LTδ为单元长度; Fδ为单元的力.假设φ和ψ(φ<ψ)为连接构件两端的节点,则关联矩阵C第γ行的元素公式(37)表示
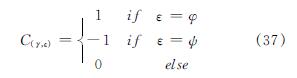
在忽略刚体位移的情况下,若切线刚度矩阵是正定的,即满足式(38)时该张拉整体结构体系是稳定的:
eig(KT)=λ1≤λ2≤…≤λσ(38)
式中,σ为最后一项.
如图1所示,Quadruplex张拉整体结构单胞由4根压杆和12根拉索组成,沿着坐标轴X轴和Y轴方向的跨度均为10 m,高5 m.图中黑色的粗线为压杆,紫色的细线为拉索,其中拉索bd、dg、gv和vb为顶部索,拉索da、gc、ve和bu为中部索,拉索ac、ce、eu和ua为底部索.表1是该单胞的节点坐标位置.表2是 Quadruplex 单胞结构的几何、材料和力学参数.
表1 Quadruplex张拉整体结构单胞的空间点坐标
Tab.1 The node coordinates of a single cell in a quadruplex tensegrity structure
在折叠过程中假设空间点a、c、e和u的位置不变,四根顶部索为主动索,四根中部索为被动索.为确定空间点在展开运动以前的初始位置,假设构件的预应力为零的情况下,对空间点d、g、v和b施加100 kN的节点外力,方向沿顶部拉索的轴线方向向外,并且当中部索的压力大于由公式(29)所求出的值时将不参与下一个时间步的计算,并且在计算的全过程中忽略顶部索长度的变化对结构的影响(如图2所示).
由图2可知,Quadruplex张拉整体结构单胞是一个中心对称的结构并受到了中心对称的力和约束条件,所以在结构展开过程中构件的运动轨迹也是中心对称.因此本文以杆件ab为例进行分析.由第1节的计算理论可知,空间点b在展开过程中的时间步数—位移大小关系(图3)和结构折叠状态下空间点的坐标(表3).
确定了空间点的在结构折叠状态下的坐标位置,即确定了结构在结构折叠状态下的形态(图4).在展开过程中,通过收缩顶部索的长度对结构进行驱动,并在中部索的长度大于其原长时开始考虑中部索的拉力对空间点的影响.在matlab中只需将100 kN的力施加到节点处,并与被动索的方向向量相乘的方式实现.
由图4可知,该结构的形态、驱动方式和约束方式沿着结构的中心对称.所以,在结构展开过程中构件的运动轨迹也是中心对称.由第一节中的计算理论可知空间点b在的折叠过程中的时间步数与位移大小的关系并与其展开时的数据作对比(如图5所示),并求出结构的展开过程(如图6所示)以及展开过程中构件预应力的变化过程(如图7所示).
由图5可知,在确定该结构初始形态时,空间点b的位移与该点在结构展开过程中产生的位移相等、路径相似.所以通过2.1小节的方法计算空间点的初始位置和结构的初始形态是可行的.
图6(a)~(d)展示了该结构展开的过程,这个过程证实Quadruplex张拉整体结构可以转化为可展结构,通过收缩顶部索的长度实现结构展开.这个过程的逆过程就是确定空间点初始位置和结构初始形态的过程.
图7 结构的展开时构件预应力的变化过程
Fig.7 The change process of prestress of the components during the expansion of the structure
表4 Quadruplex张拉整体结构单胞的空间点坐标
Tab.4 The node coordinates of a single cell in a quadruplex tensegrity structure
在结构展开的过程中,当中部索的长度小于或等于式(29)所求出的长度时,结构的ZS=0和D=12>0,此时结构变为可发生有限位移的机构; 当结构运动到最终形态时,结构的ZS=1>0和D=9>0.在忽略刚体位移的情况下,切线刚度矩阵KT的特征值如图8所示.
由图8可知,切线刚度矩阵KT的特征值大于等于零且满足式(38).所以当结构运动到最终形态时,该张拉整体结构是稳定的.
本文采用固定底部节点和缩短顶部索长度的方式驱动Quadruplex张拉整体结构进行展开运动,并得出以下结论:
(1)由图5可知,该结构在折叠与展开过程中,空间点b的位移大小相似.所以确定结构折叠形态的过程就是结构展开的逆过程.
(2)将底部节点设置为铰支座的情况下,通过调节顶部索长度的方式可驱动结构进行展开运动.在运动的过程中,由于结构的ZS=0和D=12>0,所以结构将不存在用于刚化机构位移模态的自应力模态,因此这个运动属于机构运动.但当结构展开至最终形态时,结构的ZS=1>0和DS=1>0和gt;0,即结构同时存在自应力模态和机构位移模态,并且其切线刚度矩阵是正定的,所以该结构的展开过程是一个可发生有限位移的机构转化为张拉整体结构的过程.
(3)由图7和表5可知所示,在运动结束时,结构的各个构件均获得了预应力,并经过ANSYS软件的计算中到了验证.并由结构的自应力模态数、机构位移模态数和切线刚度矩阵的正定性可知,各个构件所获得的预应力可使结构刚化.说明在驱动过程中顶部索发挥了主动索的作用,为结构中的其他构件施加了预应力.