调研发现由于历史的原因和城镇建设的发展,该城墙段现存的城墙段部分损坏,墙体面层砖酥碱、风化、离鼓较为严重,离鼓区域存在相对鼓胀情况,最大鼓胀量可达20 cm; 侧墙上存在多条垂直裂缝,侧墙上多处砌体因灰浆流失而松散、缺失; 城墙侧面有草木或藤本植物等生物病害; 墙体表面有人工干预痕迹,疑似抹灰层(图1).

图1 城墙病害分布图
Fig.1 Disease distribution map of the city wall

与传统测绘方法相比,三维激光扫描技术在不破坏古城墙现状的前提下,不仅可以获得城墙高度密集的点云数据,也能充分显示古城墙细节特征,例如对城墙细微的沉降、开裂、酥碱、风化及鼓胀变形等城墙常见病害分析^[24].因此,本文尝试运用三维激光扫描技术获得该古城墙200 m段范围内的基础点云数据,并找到城墙的病害部位,利用Geomagic Qualif软件量取城墙的破损面积,最后计算古城墙修缮所需的用砖量.经检测发现改古城墙有些地方破损严重,需要对其进行修复.例如,以该墙段L1位置为例,其点云图如图2(b)所示,在L1路线上2.8 m处,出现明显空鼓情况,外鼓距离约为16.5 cm.通过Geomagic Qualif软件计算该区域空鼓面积大约为4.12 m²,而每一块砖0.043 m²,故此处需要96块砖.

图2 城墙病害勘察
Fig.2 A survey of the disease on the wall

随机选择16处明确产地的城墙砖和该城墙上2块砖(未知产地)作为检测对象,对其进行化学组成成分检测,样本相关参数详见表1.

表1 样品参数
Tab.1 The sample parameters

由于改古城墙砖样品无法直接满足相关分析测试的条件要求.因此,在分析之前,对样品进行预处理(图3).首先,清除砖样品表面的浮尘和黏结灰浆; 其次,将城砖切割中掉下的残渣部分经锤击粗碎后,使用玛瑙研钵将其研磨成均匀粉末状,进行硼砂压片制样,以用于成分结构与红外分析^[25-27].采用Shimadzu XRF-1800荧光光谱仪对砖样品中的主要元素进行定量分析,数据采用氧化物的形式,数据见表2.

从表2中得知,由于砖的化学组成成分众多,主要含有14种氧化物成分,即SiO₂、Al₂O₃、CaO、Fe₂O₃、MgO、K₂O、Na₂O、TiO₂、P₂O₅、MnO、SO₃、ZrO₂、SrO和Rb₂O.由于这些成分之间存在高度的非线性,单纯依靠理论计算或针对某一成分进行砖产地判断的方法值得商榷.鉴于此,本文提出基于模糊相似优先比的古城墙砖范例推理方法,对影响砖产地判别的每个化学成分分别在目标范例与源范例间建立模糊相似优先关系,得到不同化学成分下目标范例与源范例间的相似性序列,找出与目标范例最相似的源范例,最终实现城墙砖产地的预测.

图3 样品制备
Fig.3 Sample preparation

表2 古城墙砖氧化物种类及含量
Tab.2 Type and content of oxide of ancient city wall brick

设B=B₁×B₂×…×B_j×…×B_n为一离散n维因素空间,B_j(j=1,2,…,n)为一实数有穷集合,则古城墙砖范例可定义为C=(b₁,b₂,…b_j,…,b_n),b_j∈B_j(j=1,2,…,n),b_j为古城墙砖的第j个化学组成成分.

而古城墙砖源范例库表示为BC={C₁,C₂,…,C_k,…,C_K},C_k∈BC(k=1,2,…,K),C_k为古城墙砖的第个源范例.城墙砖目标范例表示为C₀=(b₀₁,b₀₂,…,b_0j,…,b_0n),b_0j(j=1,2,…,n)为古城墙砖目标范例的第j个化学成分.

设C_p和C_q分别为源范例库BC中的第p个和第q个源范例,且C_p≠C_q(p,q=1,2,…,K),b_pj和b_qj分别为源范例C_p和C_q的第j个化学成分,C₀为城墙砖的目标范例,则

C_p=(b_p1,b_p2,…,b_pj,…,b_pn)

C_q=(b_q1,b_q2,…,b_qj,…,b_qn)

C₀=(b₀₁,b₀₂,…,b_0j,…,b_0n) (1)

化学成分之间的相似性度量采用化学成分之间的语义距离来表示^[28].则源范例C_p第j个化学成分与目标范例C₀第j个化学成分间语义距离为

D(C_pj,C_0j)=|b_pj-b_0j| (2)

源范例C_q第j个化学成分与目标范例C₀第j个化学成分间语义距离为

D(C_qj,C_0j)=|b_qj-b_0j| (3)

当采用两范例间的语义距离表示其相似程度时,当语义距离愈小,两个化学成分就愈相似^[28].

设城墙砖源范例C_p和C_q的第j个化学成分分别是C_pj和C_qj,它们与C₀的第j个化学成分C_0j间语义距离分别是D(C_pj,C_0j)和D(C_qj,C_0j),则C_p的第j个化学成分C_pj比C_q的第j个化学成分C_qj与C_0j的模糊相似优先比定义为

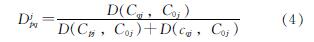
式中,D^j_pq∈[0,1],且D^j_qp=1-D^j_pq∈[0,1].D^j_pq愈大,C_p的第j个化学成分C_pj比C_q的第j个化学成分C_qj同C₀的第j个化学成分愈相似.

令p=1,q=2,3,…,K,求得D^j₁₂,D^j₁₃,…,D^j_1K; 令p=2,q=1,3,…,K,求得D^j₂₁,D^j₂₃,…,D^j_2K,依次取p,q=1,2,…,K,同时令p=q时,有D^j_pq=0,则

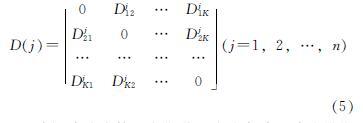
该矩阵称为第j个化学成分的古城墙砖的模糊相似优先关系.依次取j=1,2,…,n,求出对应于n个化学成分的模糊相似优先关系有n个.

对于D(j)取各λ截集,可得K个城墙砖源范例第j个成分与目标范例C₀的相似程度序列.让λ由大到小,分别检查D(j),若第p行首先出现除对角线元素为0外,其它元素皆为1,则认为C_p与C₀最相似,划去C_p所在的行和列; 同样可得与C₀相似程度排第二的城墙砖源范例,依次递推,得到城墙砖源范例库中K个源范例与C₀相似程度序列^[29].

假定:与C₀最为相似的排在序列最前,顺序号为1; 与C₀最不相似的排在最后,顺序号为K.则K个古城墙砖源范例的顺序号可组成如下序号集:

T_j=(t_1j,t_2j,…,t_kj,…,t_Kj) (6)

对应于n个化学成分就形成n个序列号集:

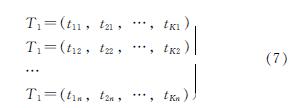
第k个城墙砖源范例与C₀相似程度序列中的顺序号为:

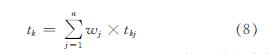
式中,w_j为n个化学成分的权重(j=1,2,…,n); 取k=1,2,…,K,利用式(8)得K个范例顺序号大小; t_k愈小,C_k与C₀愈相似,在相似程度序列中愈排前.

权重用来衡量各影响因素的相对重要性.考虑到权重对环境的敏感,在不同的决策环境下相同的因素对决策输出会有不同的影响^[30].本文根据熵值的概念,提出城墙砖化学成分权重的计算方法.

假定被评价对象有m个,即评价比较m个城墙砖; 每个被评价古城墙砖的化学成分指标有n个,则每个古城墙砖的各化学成分值构成判断矩阵R.

R=(r_ij)_m×n(i=1,2,…,m; j=1,2,…,n)(9)

对判断矩阵R进行归一化,得到矩阵B.

B=(b_ij)_m×n(i=1,2,…,m; j=1,2,…,n)(10)

B的元素为

式中,r_max和r_min分别为同一化学成分下不同产地的指标值中最大者和最小者.

按照熵的概念,定义指标的熵为

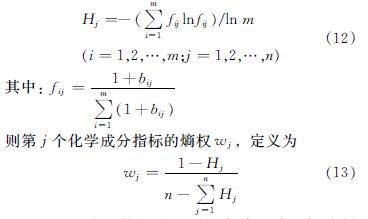
通过上述计算方法,可得古城墙砖目标范例的化学成分的权重分配,由于古城墙砖不同化学组成成分的取值不同,对应权重分配是不一样的,从而使结果与当前的评价体现了变权的思想.

表3 古城墙砖目标范例的权重
Tab.3 Weight of ancient city wall brick target example