基金项目:国家自然科学基金面上项目(51978437); 山西省高等学校科技创新项目(2019L1005)
第一作者:王夏欣(1997-),女,硕士生,主要从事钢结构研究.E-mail:799749409@qq.com 通信作者:程 欣(1986-),女,博士,副教授,主要从事钢结构研究. E-mail:xchengtyut@126.com
(1.太原理工大学 土木工程学院,山西 太原 030024; 2.长安大学 建筑工程学院,陕西 西安,710061)
(1.Department of Civil Engineering,Taiyuan University of Technology,Taiyuan 030024,China; 2.School of Civil Engineering,Chang'an University,Xi'an 710061,China)
cold-formed SHS; the effective plastic width method; ultimate capacity; local buckling; uniaxial bending
DOI: 10.15986/j.1006-7930.2021.03.012
近年来,冷弯方钢管因其良好的受力性能,环保节能及防腐效果好等优点,在建筑钢结构中得到了大量应用[1-2].随着冷成型技术的发展,冷弯方钢管实现了壁厚大于6 mm,甚至到20 mm的突破[3],拓宽了其应用范围.
计算冷弯方钢管的极限承载力时,欧洲规范(EC3)[4-5] 对钢结构的设计以截面分类为基础,根据局部屈曲对截面承载性能的影响程度将截面分为4类,分别对应着不同的设计准则,如图1所示.其中class1和class2类截面钢构件可以达到全截面塑性弯矩; class3类截面不能达到全截面塑性弯矩,但可超过边缘屈服弯矩; class4类截面由于局部屈曲的较早发生,极限承载力小于边缘屈服弯矩.对于class1和class2类截面,规范按全截面塑性计算其极限承载力,未考虑材料的强化作用; 对于class3类截面按弹性设计方法计算,未考虑其有限塑性发展,导致class2类截面和class3类截面承载力的不连续; 对于class4类截面采用有效弹性宽度法进行计算,但其计算过程较为繁琐,不利于实际操作.
采用中国规范[6-7] 计算冷弯方钢管的极限承载力时,其中《钢结构设计标准》(GB50017)[6] 采用与EC3类似的截面分类和设计方法,将截面分为S1~S5级(图1),因此设计方法与EC3存在相同的问题,且均未考虑冷弯效应.《冷弯薄壁型钢结构技术规范》(GB50018)[7] 对宽厚比较大的构件采用有效弹性宽度法进行计算,只对全截面有效的构件考虑冷弯效应.但GB50018[7] 对壁厚小于2 mm以及大于6 mm构件的设计暂无明确规定,因此有必要对各种厚度冷弯方钢管的极限承载力进行研究.
姚行友等[8] 对壁厚小于2 mm的冷弯方矩钢管开展了轴压试验,结果表明GB50018[7] 可用于该类构件的设计,但结果偏于保守.而部分学者[9-12] 对壁厚大于6 mm的冷弯厚壁方矩钢管进行的轴压试验结果表明,GB50018[7] 是否适用于该类构件的承载力设计尚存争议.据此,侯刚等[1] 、童乐为等[2] 以及沈祖炎等[13] 分别提出了适用于冷弯厚壁方矩钢管的考虑冷弯效应的屈服强度设计公式.此外,Gardner和Yun[14] 对包括冷弯薄壁和厚壁的方矩形、圆形、C形等截面的材性试验进行了汇总和分析,总结出了适用于不同厚度和截面类型的冷弯型钢材性模型.
为了解决有效弹性宽度法计算繁琐的问题,Shafer等[15] 基于截面宽厚比提出了计算冷弯薄壁型钢承载力的“直接强度法”,该方法直接采用全截面特征,考虑了多种屈曲形式下的荷载,已被列入GB50018[7] 中.王春刚等[16] 、何帆等[17] 通过试验结果比较表明直接强度法比有效宽度法计算得更为准确和简便.Yun和Gardner[18] 为了考虑class1和class2类截面材料的强化作用提出了“连续强度法”(CSM)用以计算冷弯厚壁箱形截面的极限承载力.邓家明等[19] 将CSM的应用范围扩展到了冷弯薄壁箱形截面.Nseir[20] 根据局部屈曲和承载力的相互作用提出了“整体相互作用法”(OIC).该方法可以计算包括冷弯方形、焊接方形、圆形等截面的极限承载力,不依赖于截面分类,较为明确简便.以上研究仅对冷弯厚壁方形截面或者薄壁截面进行分析,但对同时涉及薄壁和厚壁截面的承载力研究较少.
笔者[21] 提出了“有效塑性宽度法”(EPM)以计算考虑局部失稳的H形截面极限抗弯承载力.该方法基于极限状态时的截面应力分布特点,假定有效截面能够全部发展塑性,不受截面分类限制,具有良好的适用性.因此可从截面应力分布特点出发,突破壁厚限制,将EPM的应用范围扩展到不同厚度的冷弯方形截面.
本文建立了考虑几何和材料非线性的Abaqus有限元模型,对冷弯箱形截面在轴压和压弯作用下的极限承载力进行研究,提出了用于计算极限承载力的有效塑性宽度法.
为了研究冷弯方形截面的承载性能,对已有试验进行汇总和分析,以校核有限元模型.侯刚[13] 和Nseir[20] 分别对不同截面尺寸的冷弯箱形截面钢构件进行了轴压试验,其中Nseir[20] 还开展了不同偏心距的偏压试验.加载前对各试件的初始几何尺寸、残余应力、材性等进行了测量; 加载时,侯刚[12] 采用一端固定,另一端滑动铰接的边界条件,Nseir[20] 采用两端铰接的边界条件; 通过加载得到了各试件的破坏模态、荷载-轴向位移曲线和极限承载力等.试件的基本信息见表 1.冷弯箱形截面的几何尺寸定义如图2所示,其中b和h分别为截面的宽度和高度,t为截面厚度,弯角内径为2t,e为加载点偏离形心轴x轴的距离,l为试件的实际长度.
为了研究冷弯方形截面在轴压和压弯作用下的承载性能,采用Abaqus对图3所示三种加载模式的构件进行了有限元模拟.包括了对轴压构件在柱顶截面中心施加竖向力N(图3(a)),对偏心受压构件在距柱顶截面中心e处施加竖向力N(图3(b)),以及对悬臂压弯构件在柱顶施加常轴力N和侧向水平荷载V(图3(c)),其中u和Δ分别为轴向和侧向位移.
对于压弯作用,图3(b)主要用来验证有限元模型在压弯状态下的准确性.图3(c)的加载模式可直接确定特定轴压力水平下的截面抗弯承载性能及最大弯矩在构件上的作用位置,因此参数分析时采用了图3(c)所示的悬臂压弯加载方式.
单元类型采用S4R壳单元(四节点四边形有限薄膜应变线性缩减积分壳单元),该单元能够体现板件的复杂屈曲行为,在大多数情况下能够提供准确的模拟[22].
为了研究网格尺寸对构件承载力的影响,对部分典型试件分别进行了网格尺寸为15 mm×15 mm、12 mm×12 mm、10 mm×10 mm、8 mm×8 mm以及6 mm×6 mm的网格敏感性分析,结果如图4所示,发现网格尺寸对极限承载力影响较小.因此综合计算精度和时间成本,平板处网格尺寸采用10 mm×10 mm,弯角处较精细地划分为4个网格,如图5所示.
图6 Gardner和Yun[14] 材料模型
Fig.6 Material model in Gardner and Yun[14]
为了考虑局部初始几何缺陷的影响,首先在模型上施加轴力进行线性特征值屈曲分析,得到规定数目的屈曲模态,并从中选择相应的屈曲模态作为初始几何缺陷施加到构件上.对试验进行验证时,选择与实际初始缺陷相近的屈曲模态,缺陷的幅值采用实测几何缺陷的最大值,对于未测量初始缺陷的试件,采用与参数分析相同的方法施加初始缺陷; 参数分析时选择沿柱长有奇数个屈曲波的第一屈曲模态(最不利模态)[13],缺陷的幅值根据欧洲规范EC3-1-5[5] 对局部屈曲幅值的规定取截面边长的1/200.
冷弯方形截面的纵向残余应力主要包括弯曲残余应力和薄膜残余应力.材性试验的试样拉伸时弯曲残余应力已被考虑在其中[18],而薄膜残余应力与弯曲残余应力相比,数值很小而可以忽略,因此本文建立的有限元模型不添加残余应力.
在构件底部用Kinematic coupling将截面的所有节点耦合在截面中心(轴压和悬臂压弯受力状态)或偏心(偏压受力状态)参考点RP-1上; 在构件顶部用Rigid body将截面转化成刚面,以防止应力集中导致的板件压溃,并将截面的所有自由度赋予在中心或偏心参考点RP-2上,如图5所示.
对于轴压和偏心受压构件,约束RP-1三个方向的平动自由度以及非弯曲方向的转动自由度; 约束RP-2除竖向位移和非弯曲方向的转动自由度.加载时,将轴力施加在RP-2上,并通过弧长法进行分析.
对于悬臂压弯构件,约束RP-1的所有自由度,释放RP-2的所有自由度.加载时,首先以力加载的方式在RP-2施加常轴力N,随后以位移加载的方式在RP-2施加水平位移Δ,通过静力通用方法进行分析.
提取出有限元模型的破坏模态和荷载-位移曲线与试验结果进行比较,分别如图7和图8所示,极限承载力的对比结果如表 1所示,发现有限元模型能较准确地模拟出冷弯箱形截面的破坏模态、极限承载力及曲线的全过程走势.因此后续可用该模型进行参数分析.
本文对冷弯方钢管进行参数分析,取h=b.板件宽厚比r和轴压比n是影响冷弯方形截面承载力的两个主要因素,其定义如下.
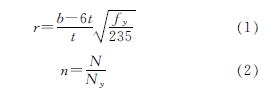
式中:r为平板处的宽厚比[4],Ny为轴压屈服荷载,Ny=A·fy,其中A为全截面面积.
参数分析时钢材牌号为Q355钢,弹性模量E=206 GPa,泊松比ν=0.3.固定截面中心线长b-t=200 mm,截面弯角内径为2t,构件长度l为3b.通过改变截面厚度t和轴压力N,实现宽厚比r和轴压比n的变化.
宽厚比r取15~150范围中5的倍数,共28个截面.对该28个截面分别进行了轴压分析和不同轴压比的压弯分析.压弯构件在n≥Nu/Ny(Nu为构件的极限抗压承载力)时不具有抗弯承载力,因此Nu可用来确定压弯分析时轴压比的上限值.压弯参数分析中n的具体取值见表 2.轴压和压弯参数分析范围内共有214个有限元模型,包含了实际工程中可能会出现的大多数情况.
用python语言在py charm环境中编写改变t和N的程序,并通过Abaqus command实现该程序与Abaqus的数据交流,以自动进行参数分析.
根据参数分析结果发现,冷弯方形截面在轴压和压弯作用下的破坏模态均由局部屈曲控制.其中轴压构件的破坏模态如图9(a)所示,截面的四边板件都发生了局部屈曲; 压弯构件的破坏模态如图9(b)所示,其典型破坏模态为近柱底部位的局部屈曲.
以宽厚比为80的轴压构件为例,其在柱中部位发生了较大的局部屈曲而破坏,提取模型屈曲变形最大截面的平均应力发展过程研究其破坏机理,如图 10所示,由于应力是对称分布的,只给出了相邻两边板件的应力发展图.当轴压力较小时(A点和B点),板件未屈曲,压应力在整个截面均匀分布.随着轴力增加(C点和D点),由于板件较薄,在弹性状态下发生了局部屈曲,板件中部产生了鼓曲变形,中部平均应力开始下降,而角部区域由于相邻板件相互支撑的作用保持挺直,其上平均应力保持稳定增长.随着轴力的增加,局部屈曲进一步发展,达到峰值承载力(E点),此时板件中部的应力几乎为0,可认为这部分板件已经退出工作,为失效区; 角部区域仍然保持一定的应力,为有效区.
典型压弯构件(宽厚比为80、轴压比为0.2)在靠近柱底部位发生了局部屈曲而破坏.提取其屈曲变形最大截面的平均应力进行分析,如图 11所示.图中A点为只有轴力作用下的应力.施加侧向位移后(B点和C点),受压翼缘的压应力进一步增大,受拉翼缘由受压转为受拉状态,腹板变为部分受拉部分受压状态.随着侧向位移的增加(D点),受压翼缘发生了屈曲变形,板件中部应力下降,角部应力保持增长.达到承载力峰值(E点)时,受压翼缘中部应力几乎为0,为失效区,角部区域仍然保持一定的应力,为有效区; 此时腹板的受压区发生了局部屈曲,应力呈现下降的趋势; 受拉翼缘的拉应力仍稳定增长.继续施加侧向位移(F点和G点),受压翼缘和腹板的受压区屈曲变形进一步增大,受压翼缘和腹板受压区的失效区进一步扩展,角部区域仍然保持一定的应力.
不同宽厚比和轴压比的构件,在极限状态时会发生不同部位及不同程度的局部屈曲,即局部屈曲是导致承载力到达峰值,不再增长的主要原因.宽厚比主要通过影响发生局部屈曲时的临界应力来影响极限状态,而轴压比通过影响截面的应力分布,进而影响局部屈曲的发生时刻而影响极限状态.
通过对不同宽厚比和轴压比构件的应力发展图进行分析后发现,极限状态时局部屈曲会导致截面出现失效区,并且随着宽厚比和轴压比的增大,失效区会提前出现并出现扩大的趋势.
为了得到冷弯方形截面极限承载力随轴压比和宽厚比的变化规律,从参数分析结果中提取极限抗压承载力Nu和极限抗弯承载力Mu,分别采用Ny和Mpc进行无量纲化,如图 12所示,其中Mpc为考虑轴压力作用的全截面塑性弯矩.
从图 12(a)中可以看出,Nu/Ny随着宽厚比的增大而减小.宽厚比较小时,Nu/Ny≥1,说明极限时能够达到或超过全截面塑性; 宽厚比较大时,Nu<Ny,极限时由于局部屈曲的发生,截面只能发展部分塑性.
从图 12(b)中可以看出,Mu/Mpc随着宽厚比的增大而减小.对于宽厚比较大的构件,轴压比的增大会导致局部屈曲的提前发生,因此随着轴压比的增大而减小.对于宽厚比较小的构件,极限状态时,截面能达到全塑性且能够发挥不同程度的强化作用,但Mpc随着轴压比的增长下降速度变快,因此会发生Mu/Mpc随轴压比的增大而增大的情况.当Mu/Mpc≥1时,对应图中切面的上半部分,截面能达到全截面塑性弯矩; 当Mu/Mpc<1时,截面只有部分区域能够发展塑性.
为了考虑局部失稳对H形截面钢构件极限承载力的影响,笔者[21] 提出了有效塑性宽度法(EPM),该方法基于构件的破坏模态以及极限状态时截面的应力分布特征,得到了不同宽厚比和轴压比下有效宽度的变化规律,通过计算有效宽度的塑性弯矩得到H形截面钢构件的极限抗弯承载力.本文提出了适用于15≤r≤150的冷弯方形截面极限抗压和抗弯承载力的有效塑性宽度法.
轴压状态下,对于宽厚比较小的截面,当承载力达到极限状态时截面能够达到全截面塑性.对于宽厚比较大的截面,由于局部屈曲的发生,极限状态时板件中部应力接近0,可视为失效区; 角部区域由于相邻板件的相互支撑作用,平均应力接近屈服应力,为有效区.基于此,假定极限状态时有效截面及应力分布如图 13所示,为了简化计算,将截面的弯角简化为直角.根据该应力分布形式,得到冷弯方形截面极限抗压承载力计算公式为
Nu=ρ1Afy (3)
其中,ρ1为轴压下板件的有效宽度系数,ρ1=(34)/r+0.15≤1,当全截面有效时,ρ1=1.
压弯作用下达到极限状态时,对于有局部失稳发生的截面,在不同的宽厚比和轴压比组配下会产生不同的屈曲形式,根据有效截面及应力分布形式的不同分为四种情况,分别如图 14(a)~(d)所示.
图 14 压弯构件有效截面及应力分布模型
Fig.14 The effective section and stress distribution model for members under axial force and bending
(1)当轴压力较小时,假定轴压力产生的压应力只分布在腹板上.极限时,受压翼缘和腹板均发生局部屈曲而出现失效区,有效宽度分别为be1和be2; 受拉翼缘为完全受拉状态,全部有效,如图 14(a)所示.其中,受压翼缘应力分布与在轴压作用下的分布相同,因此假定其有效宽度相等.应力对x轴取矩可得Mu的计算公式为
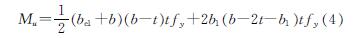
其中腹板处拉应力的宽度b1根据轴压力的平衡条件按下式计算.
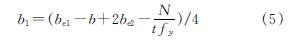
(2)随着轴力的增长,轴压力产生的压应力向受拉翼缘方向延伸,分布在腹板和受拉翼缘上,但未扩展到受压翼缘区域.极限时,受压翼缘和腹板由于局部屈曲的发生而部分有效,受拉翼缘全部有效,如图 14(b)所示.Mu的计算公式为
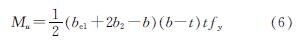
其中受拉翼缘拉应力的宽度b2为
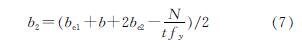
(3)随着轴压力的进一步增长,轴压力产生的压应力分布在腹板、受拉翼缘和受压翼缘上.极限时,受压翼缘和腹板部分有效,受拉翼缘全部有效,如图 14(c)所示.此时较图 14(b),腹板的有效宽度进一步减小,受压翼缘和受拉翼缘的受力状态基本不变.计算可得Mu为
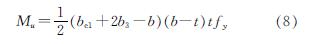
其中受拉翼缘拉应力的宽度b3为
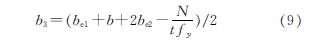
(4)当轴压力接近极限抗压承载力时,受压翼缘、腹板和受拉翼缘在轴压力和弯矩作用下均发生了局部屈曲,出现失效区,如图 14(d)所示,其中受拉翼缘有效宽度为be3,有效宽度的应力为f1.此时受拉翼缘的应力分布可等效为应力均为fy的部分受拉部分受压的分布形式,与图 14(b)、(c)相似,Mu的计算公式为
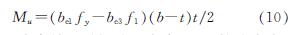
其中受拉翼缘有效区承担的压应力f1计算公式为
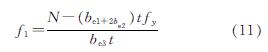
对于图 14(b)~(d)的情况,将b2、b3和f1分别代入相应的Mu计算公式中,发现此三种情况下Mu的计算公式相同,主要原因是这三种情况腹板均全部受压,弯矩可直接由上下翼缘的应力差值取矩得到.因此对以上四种情况,以轴力产生的压应力是否深入到受拉翼缘为界(该界限值为Nwcr),分成两种情况,如式(14)所示.
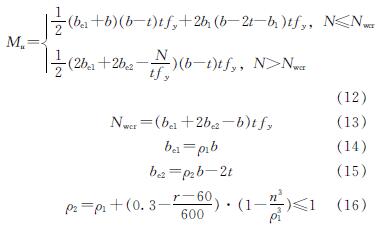
当n=ρ1时,代入到式(3)中可得到N=ρ1Afy=Nu,即Mu=0; 代入到式(14)中也可得到Mu=0,并且图 14(d)的应力分布模型也可回归到图 13上,说明EPM能将压弯情况完全回归到轴压情况,理论意义良好.
本节通过对EPM与EC3[4] 、GB50017[6] 、GB50018[7] 以及有限元结果(FE)进行对比,验证其准确性,并对其进行评价.
按照上述四种方法计算的极限抗压承载力和有限元的对比结果如图 15所示.可以看出,EPM、EC3和GB50017与有限元结果均非常接近,而GB50018则较为保守.
上述四种方法计算的不同轴压比下的极限抗弯承载力和有限元的对比结果如图 16所示,现行规范对极限抗弯承载力的计算均偏于保守,其中GB50018的计算结果最为保守.而本文所提的EPM最接近有限元结果.
将四种计算方法与有限元结果比值的平均值和方差分别列于表 3中,比较结果显示,现行规范较为保守地估计了截面的承载力,其中EC3比较接近有限元结果,EPM与有限元结果最为吻合,较为有效地改进了规范的计算结果.
本文提出的EPM基于极限状态时截面应力的物理模型计算承载力,反映了构件的真实受力情况,因此能够给出较为准确的计算结果.该方法不依赖于截面分类,突破了截面类别对极限承载力的限制,可体现class3类截面发展部分塑性的能力以及class4类截面弹性局部屈曲的影响,且概念明晰,操作简便,便于工程人员采用.
本文对轴压和压弯作用下的冷弯方钢管进行了有限元模拟,考察了轴压比和宽厚比对冷弯方钢管极限承载力的影响,得出以下结论:
(1)宽厚比和轴压比是影响极限承载力的决定性因素.不同宽厚比和轴压比的构件极限状态时由于局部屈曲的发生板件会出现不同程度的失效,从而导致极限承载力不同.
(2)本文基于破坏模态和应力发展过程提出了冷弯方形截面在轴压和压弯作用下极限状态时的四种不同的应力分布模型,并且最终能回归到轴压情况,理论意义良好.
(3)基于截面应力分布模型提出了计算冷弯方形截面极限承载力的有效塑性宽度法,该方法不依赖于截面分类,且计算简单,便于操作.
(4)现行规范对于冷弯方形截面极限抗弯承载力的计算比较保守,而有效塑性宽度法可以提供相对准确的承载力计算结果.