基金项目:安徽交通控股集团交通科技项目(JKKJ-2021-4); 安徽省交通运输厅科技进步计划
第一作者:吕韶全(1988-),男,硕士,高级工程师,主要从事公路路基工程的科研及项目管理工作.E-mail:690886502@qq.com
(1.安徽交通控股集团有限公司,安徽 合肥 230088; 2.中国地质大学(武汉)工程学院,湖北 武汉 430074)
(1.Anhui Transportation Holding Group Co.,Ltd.,Hefei 230088,China; 2.Faculty of Engineering,China University of Geosciences,Wuhan 430074,China)
soil arching effect; three directional stress state; theoretical model; numerical simulation; model test
DOI: 10.15986/j.1006-7930.2021.04.007
土拱效应是岩土工程中存在的一种普遍效应,Terzaghi最先通过活动门的实验所证实[1].由于土体受力土颗粒产生相对位移而产生的应力偏转现象进而形成土拱效应,土拱产生的机理是土的不均匀位移,使土颗粒相互“楔紧”[2].查明土拱作用的规律对斜坡防护的抗滑桩工程达到最大的安全程度与最大的经济效益具有重要的指导意义[3].
在土拱形成机理上,学者展开过大量的研究并取得了丰富的理论研究成果.王成华[4]等提出的桩间距计算模型是基于以抗滑桩桩侧的侧摩阻力为主要支撑的桩间土拱,他考虑了土拱后的被动土压力; 周德培[5]等从桩的两侧土拱相交的等腰三角形区域着手,认为三角形区域是土体最容易破裂的地方,等腰边为潜在破裂面; 贾海莉[6-7]等认为桩后拱与桩侧拱是重合的,并认为桩间距只与土体的性质有关,与荷载的大小无关,并建立了桩间距的计算模型; 郑磊[8]等考虑了土拱自身的抗力,但推导式中并未作说明; 赵明华[9]等基于桩侧土拱理论推断,未考虑土体自重,考虑了桩间斜拱的情况; 李长冬等[10]的改进桩间距模型是假定滑坡体前缘平缓而计算的土拱与滑动面所产生的摩擦力,建立了的桩侧摩阻力与滑动面所产生的摩擦力承担滑坡推力的关系式,文献[11-17]对土拱效应进行了二维数值模拟研究,文献[18]进行了土拱效应三维理论分析,认为轴应力是最大主应力,未考虑桩两侧都有土拱,具有一定的局限性; 此外,张永兴等人[19-24]对于成拱与拱的破坏的影响因素也开展了大量数值模拟研究,认为考虑自重应力对土拱效应的影响是显著的.
既有的研究多数基于二维平面模型,对拱脚破坏面进行假定的形式.本文通过借鉴Terzaghi等地基承载力理论,在受压区形心建立力的平衡关系进行改进,在考虑土体自重的影响下基于Drucker-Prager屈服准则建立三维土拱效应理论模型.通过ABAQUS有限元软件进行验证,探究三向应力状态下土拱效应的影响因素.
(1)鉴于土受压能力较受拉能力强,假设拱轴线为合理拱轴线,土拱任意截面的剪力和弯矩均视为零.以左拱脚为起点,离拱脚水平距离和竖直距离分别为x和y轴建立平面直角坐标系,拱轴线满足合理拱轴线方程:
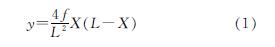
式中:f为土拱高度,L为土拱跨度.
(2)假定土拱后面的推力沿着拱轴线方向均匀分布.
(3)二维平面的研究,简化土拱的分布形态,仅讨论单位厚度的土拱.
考虑桩两侧都有土拱分布,在桩端形成一个三角形受压区(地基承载计算中为楔形区),对形心B受力分析如图1所示,三角形受压区受到两边土拱拱轴力,受到桩的支撑反力,三力平衡.在对形心应力状态分析时,将轴力分解为水平方向与竖直方向,土力学规定压应力为正,拉应力为负,则竖直方向与水平方向为两个主应力σ1与σ2方向.由图1可知:

其中β为土拱在桩端处切线与水平线的夹角,也是破裂面与桩的夹角,其值大小与桩土摩擦系数有关,若桩看成光滑,根据莫尔库伦原理可知,潜在滑动面与最大主应力夹角为45°-φ/2,若桩土摩擦系数大于土的tanφ,那么β值与φ值相等,即桩土摩擦角与土的内摩擦角相等,一般情况下,据文献[25-26]黏土与混凝土桩摩擦系数为0.3,近似将桩侧面看成光滑.

其中:q为拱后均布荷载; L为桩间距; f为拱高; F轴为土拱轴力; Fx、Fy分别为轴力在水平方向与竖直方向的分力.
将式(3)、(4)带入(2)求得σ1、σ2,在形心B处取微小的三角形单元,如图2所示,其中AC为破裂面,AC外法线方向与x轴夹角为θ,可根据桩土摩擦系数确定,由于x,y方向为主应力方向,所以-τ1=-τ2=0,于是AC面上有
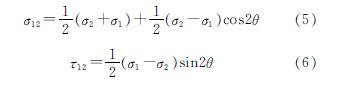
根据所求的σ1,σ2,联立(5),(6)式即可求出AC破坏面上的正应力与切应力,从而根据土的抗剪强度理论建立平衡关系求出在一定的土体条件与滑坡推力下的合理桩间距.
基于上述平面状态下的理论改进建立土拱效应三维力学模型,在竖直方向上取极小长度dz的土体,在桩后微小层土体的三角形受压区的体心B取微小的六面体单元,单元体所受三个方向的应力分别为σ1、σ1、σz,应力状态如图3所示.
考虑土拱效应的三维空间问题就是考虑土拱沿桩深度的变化,假设土拱拱后推力呈矩形分布,其均布荷载为q/kPa,在深度z方向取无限小长度dz,则
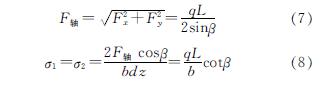
考虑自重应力的影响:
σ2=γz (9)
其中γ为土的重度; z为土在竖直方向的深度.
三向应力状态下可考虑具角隅性质莫尔-库伦破坏准则,鉴于破坏面导数方向的不确定性,分析时运用圆滑式莫尔-库伦破坏准则,即Drucker-Prager破坏准则:

其中α、k是Drucker-Prager破坏参数,其值与土的黏聚力c及内摩擦角φ有关.
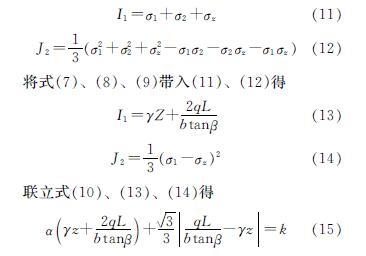
由(15)式可知:
(1)当(qL)/(btanβ)≥γz时,假设根据Drucker-Prager所得的临界深度为z0,求得
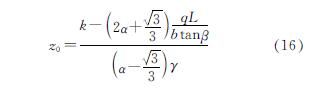
若σ1=σ2=(qL)/(btanβ)≤k/(3α)成立,则z0满足上式条件,即在0≤z≤z0深度段,三向应力状态下的土拱效应属于不利深度,主要为剪胀效应破坏土拱效应,位于上部土体有向上拱的趋势,在z0≤z≤(qL)/(bγtanβ)深度段,土自重有利于土拱效应的形成; 若σ1=σ2=(qL)/(btanβ)≤k/(3α)不成立,则三向应力状态下在此深度段土拱效应不能形成或由于应力过大而失效,土会发生桩间扰流现象.
(3)当(qL)/(btanβ)<γz时,
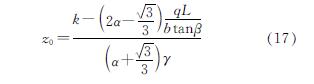
若σ1=σ2=(qL)/(btanβ)<k/(2α)成立,则z0满足上述条件,即在(qL)/(bγtanβ)≤z<z0深度段,自重效应有利于土拱效应的形成,但在z0≤z<∞深度段,土拱效应的破坏主要是自重应力,在此深度段自重应力对拱脚的破坏起主导作用; 若σ1=σ2=(qL)/(btanβ)≤k/(3α)不成立,则三向应力状态下在(qL)/(bγtanβ)<∞深度段自重应力对拱脚的破坏起主导作用,土拱效应不能形成.
土拱效应的形成具有空间效应,要形成土拱效应使桩后土体稳定,水平应力σ1与σ2需要满足σ1=σ2=(qL)/(btanβ)≤k/(3α),能在平面形成土拱效应的同时考虑自重应力的影响,根据2.3的分析可知,在自重应力的影响下对形成土拱效应的有利深度段为

在此深度段之上,土体有向上运动的趋势破坏土拱效应,在此深度段之下,自重应力对土拱拱脚的破坏起主导作用,土拱效应不能形成.在实际中,如果坡前临空面过于陡峭,此原因可导致边坡发生自重垮塌.
基于三向应力状态下土拱效应的理论探讨,运用ABAQUS对土拱效应进行三维数值模拟研究.
考虑到实际状况,在建立有限元模型时不考虑桩前被动土压力,将桩截面长度定为b,桩间距L定为5 m,为更好的研究土拱效应在z方向上的变化,将桩自由端深度定为15 m,如图4所示.为了完整模拟桩后三角形受压区受力特性及考虑桩的对称特征,模型采用沿x方向分布的2根1/2桩,中间为整桩,垂直于x方向的两个面约束x方向的位移.为探究三维尺寸中土拱效应,桩与土体可设置为光滑接触,土体与岩体接触面则采用摩擦接触.为验证在土上拱作用下造成上部土拱效应破坏,垂直于z轴的上顶面不设约束,在y负方向垂直y轴平面施加均布荷载40 kPa,考虑模型的精确与计算方便在z方向上均布网格,y方向上靠近桩端细化网格,远离y方向粗化网格,在x方向上全程细化网格,岩体,土体及抗滑桩物理力学参数取值见表1.
通过对土拱从形成到开始出现微小位移的时间段进行模拟,研究三向应力状态下土拱空间分布规律及从土拱形成、发展到破坏的过程,揭示土拱完全形成时,不同深度下矢跨比的变化规律.由于土拱效应的形成是土颗粒的不均匀位移,肉眼无法鉴别,模拟时采用y方向的主应力变化进行判断.切取z=0,z=5,z=10,z=15位置应力σ2云图切片,如图5所示,桩间红色部分为主应力σ2减少部分,其形状为拱形,代表红色区域后形成了土拱,土拱效应将滑坡推力传递到拱脚再传递给桩,红色拱形区域拱顶与桩间的距离可看成拱高f,如图所示,红色拱区域拱高f与深度z有明显的变化,为准确测量形成土拱的拱高f与沿深度z方向的变化规律,作不同深度下,离桩不同距离的应力σ2沿x轴变化规律图,如图6所示.
由于模型建立的y轴与滑坡推力方向相反,σ2呈负值,在模拟中当应力增加到0.2 kPa时在桩后可见明显的土拱效应,σ2沿x轴方向呈M形分布,远离桩σ2分布逐渐趋于平缓,此时土拱效应消失,图中曲线趋于平缓的y坐标值就是拱的矢高.总体来说,在矩形荷载分布下土拱的矢高沿深度变化不大,z=15 m拱矢长度略大于z=5 m时拱矢长度,这就意味着相同推力下,自重应力对拱的形状影响不大,y=4、5、6 m中应力线已经接近于直线,相差不大,本次模拟拱的矢高取3.5 m,即tanβ=4f/L=1.72.
借助ABAQUS后处理功能的位移增量探究土拱效应从形成到破坏在水平方向上的分布规律,验证基于二维平面上土拱效应理论的创新性研究.水平方向上位移增量分布如图7所示,水平方向上的位移增量主要是沿y轴方向的位移,即ABAQUS中的u2,如图所示,当深度5 m(z=10)处桩间土体发生微小位移时,在深度10 m(z=5)处桩间土体已经严重变形,破坏面呈M形分布,说明桩间土拱效应破坏滑动面与地基沉降破坏面相似,验证了将地基沉降理论运用到土拱效应中的可行性,桩中间土体的位移大于桩两侧土体的位移,此时土拱效应失效,桩间土发生绕流,进而验证了三向应力状态下,大于深度h时,自重应力对拱脚的破坏起主导作用,但在深度15 m(z=0)处土体未从桩间挤出,这是因为在建立模型时,考虑了土体与岩体滑面之间的摩擦,两接触面之间设为摩擦接触.其中h为:
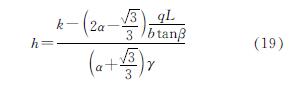
考虑到实际情况,在建立模型时将坡表面不设边界条件,探究在滑坡推力作用下土体在竖直方几上的运动规律,分别采用法线为x,y,z轴的u3位移云图切片来研究,法线为z轴模拟结果如图8所示,土体的竖向位移主要发生在桩后一小部分区域,桩间土竖向位移很小,所以竖向位移是导致桩后拱脚破坏的重要因素,越靠近桩顶,土体的竖向位移越大,深度2.5 m(z=12.5)竖向位移减少一半,到深度为5 m(z=10)时竖向位移可忽略不计,这也验证了在土体表面土拱的破坏主要是由于土向上拱导致拱脚破坏而失效.
法线为x轴模拟结果如图9所示,由于桩间土拱效应具有对称效应,所以只取z=0,z=4,z=8截面云图,桩间土体z=4较桩端土体位移小,桩端土位移形状与地基土体沉降破坏面相似,据Prandtl-Reissner理论公式可推断,靠近桩部分破坏面形状为对数螺线,远离桩部分为直线被动朗肯区,进而证明了表层土拱效应是由于σz太小,三向应力处于未平衡状态,拱脚土体向上拱,呈现与地基沉降Prandtl-Reissner理论的反向位移.
法线为y轴模拟结果如图 10所示,靠近桩部分土体在竖直方向上也有明显的成拱效应,在远离桩土体竖直成拱效应逐渐消失,在y=0云图中可见下方土体有明显的y轴负位移,进而验证了超过深度h部分土体拱脚的破坏主要是由于土体的自重应力引起.
Prandtl指出受铅直均布荷载作用的、底面光滑的无限长的条形刚性板置于土体表面,当刚性荷载板下的土体处于塑性平衡状态时,其破坏模式如图 11所示,基础底面下土体为楔形,与水平夹角为45°-φ/2,此楔形区最大主应力方向σ1为竖直方向,此区为主动朗肯区,基础侧面三角形区域为被动朗肯区,与水平面夹角为45°-φ/2,两区之间为过渡区,滑移线为对数螺旋线,两基础间滑移线呈M形分布.假设土体不动,对桩施加作用力向土体方向运动,如图所示,笔者认为桩间土拱效应问题与基于平面上的地基承载力问题本质上这相似的.
由于模拟过程中施加40 kPa应力土拱效应被破坏,再次使用20 kPa模拟,其结果与第一次模拟过程中土拱产生微小位移时的云图相似,只是应力大小发生改变,限于篇幅,所以第二次模拟结果在这里不做展示,其计算结果直接与图做比较.
图 11 Prandtl-Reissner地基极限承载力理论示意图
Fig.11 Schematic diagram of Prandtl-Reissner's ultimate bearing capacity of foundation
如图,据Prandtl-Reissner理论可知

其结果与不考虑桩土摩擦的数值模拟结果相同,下面模型验证计算tanβ取1.75.
根据Drucker-Prager破坏准则:
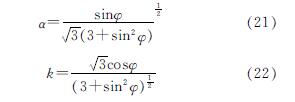
将c,φ值代入式(20)中得α=0.16,k=24.96,据2.3节可知土拱是否被破坏需满足式:

由式(23)得到q≤22.75 kPa(本文中所取的α,k值是任何π平面上莫尔-库伦破坏面的下限,所得的q值过于保守,在实际中最好用真三轴仪直接测定),所以在20 kPa模拟过程中土拱整体上未被破坏,再根据式(18)求得土拱效应存在深度为2.14≤z<2.91,深度大于2.91 m时,自重应力对土拱拱脚的破坏起主导作用,在实际中也可以看作土的自重失稳,其结果与数值模拟结果图相似,云图中深度为5 m时沿y中负方向桩间土已发生明显的位移(实际模拟中深度3 m已经开始位移,与计算值吻合),土拱开始破坏,到深度为10 m时y方向增量位移云图可清晰见到呈M字的滑动面的存在,图中的滑动面形状也与地基承载力破坏形状相同,上述三点不仅验证了理论计算结果,同时也说明了将土拱效应与地基承载力理论类比的可行性,这也许是研究土拱效应的新的思路,同时理论研究中认为z<2.14m时,土拱效应也将失效,数值模拟也验证了该结论,如图所示,但结果与模型试验结果有些许出入,2 m深度上的土体发生了明显的沿z轴正方向的位移,但土未从桩间滑出,其原因可能是在发生z轴正方向位移后,经过应力的短暂调整再次形成土拱效应来阻止桩间土绕流,但实际工程中桩间上部土容易垮塌,原因是土的上拱剪胀作用使土疏松发生桩间绕流.
在讨论三向应力状态下土拱效应时,不仅要考虑由自重效应引起拱脚破坏的深度,还要考虑土表面部分的上拱段,在施工悬臂式抗滑桩时,要注意自重效应引起拱脚破坏的临界深度.
(1)基于Prandtl-Reissner地基极限承载力理论,建立了一种新的土拱效应力学分析模型,改进了拱脚破坏面的研究假设,提出了根据桩土摩擦系数求得拱脚破坏面的新思路.
(2)基于建立的土拱效应力学分析模型,利用Drucker-Prager土的塑性破坏准则得出三向应力状态下土拱效应存在形式,在z1、z2中间深度段是土拱效应形成的有利深度段,此段中自重应力可增加土的抗剪强度,低于临界深度z1,或大于临界深度z2时,自重应力是引起土拱效应破坏的主导因素,低于临界深度时土的剪胀效应破坏拱脚,高于临界深度时由于土的剪切破坏拱脚失效.
(3)采用ABAQUS有限元模拟软件验证了三向应力状态下土拱理论模型的正确性,结论表明在竖直方向上也有成拱效应,矩形荷载作用下,土拱效应的拱的形状在竖直方向有变化,但变化不大,利用位移增量得出土拱效应失效桩间土为M形破坏,与地基破坏形状相似.