De Vries导热系数模型考虑温度的影响,但对其他类型土不一定适用.Campbell模型反映了含水率、温度与土体导热系数的关系,但对高温土体的预测并没有那么准确.de V-1和de V-2模型两个改进模型涉及参数众多,且依赖界限含水率.
IPCHT模型以自洽近似理论模型为基础,即将土分解为由固液气三相构成的介质.假定各单相分散在等效均质的连续基体中,由自洽近似理论模型推求出三相介质的等效导热系数λeff.因此提出考虑传质增强因子ξ的颗粒间接触传热(IPCHT)修正模型,考虑到温度变化范围较大,等效导热系数λeff分为两种情况:

式中:λ1,θ1为土中固相的导热系数及体积分数; λ2,θ2为土中液相的导热系数及体积分数; λ3,θ3为土中气相的导热系数及体积分数; ξ为传质增强因子; t为摄氏度(℃); λda为干燥空气导热系数; λs为土体固相颗粒导热系数; Ke为Kersten系数,Sr为饱和度; λq为石英导热系数,参考De Vries[7](1963)取8.8 W·m-1·K-1; θq为石英体积分数; λo为其他矿物的导热系数,参考刘晨晖等[19](2011).由计算可知,上海黏土固相颗粒导热系数λs为4.86 W·m-1·K-1; ψ为水势(kPa); MW为水的摩尔质量; ρW为水的密度(103 kg·m-3); R为绝对气体常数; T为开尔文氏温度(K); Pb,Pvs分别为大气压和饱和蒸汽压(kPa); gl(l=-1~4)为形状因子,g-1=-0.58×104; g0=1.39; g1=-0.05; g2=0.42×10-4; g3=-0.14×10-7; g4=6.5.由叶为民[20-21](2005)上海粉质黏土的土水特征曲线推求土中水势ψ.
图7 不同温度下土壤导热系数测定值与预测值的比较
Fig.7 Comparison of measured and predicted values of soil thermal conductivity at different temperatures
图7表示未经修正的IPCHT模型在不同温度下土壤导热系数测定值与预测值的比较结果.由图可知,非饱和黏土在低于90℃下的导热系数的测定值与预测值符合程度较高; 90℃时导热系数的预测曲线与实测曲线出现较大差值.而不同温度下的饱和黏土,实测值与预测值略有差异,说明未经修正的IPCHT模型对低于90℃的非饱和土拟合效果较好.笔者认为,上海黏土试样在高温时潜热效果较明显,而未经修正的IPCHT模型没有考虑潜热的影响,因此预测值会低于实测值.所以上海黏土在90℃的等效导热系数需考虑传质增强因子ξ,根据上海黏土土壤质地取2.5.
图8 经传质增强因子修正后实测值与预测值的比较
Fig.8 Comparison between measured value and predicted value after mass transfer enhancement factor correction
此外,使用均方根误差(RMSE)对模型进行了评价:
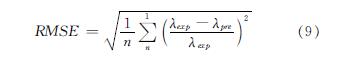
式中,λexp为实测值; λpre为预测值.
图8为经传质增强因子修正后实测值与预测值的比较.由图可知,经传质增强因子ξ修正后,90℃时上海黏土导热系数预测值和实测值相符地较好,非饱和黏土土模型修正后均方根误差为20%.而对于饱和上海黏土,IPCHT模型的预测效果不是很理想,因此寻找适合饱和上海黏土导热系数的模型,建立不同温度下上海黏土导热系数与电缆载流量的有限元模型是下一步的研究目标.