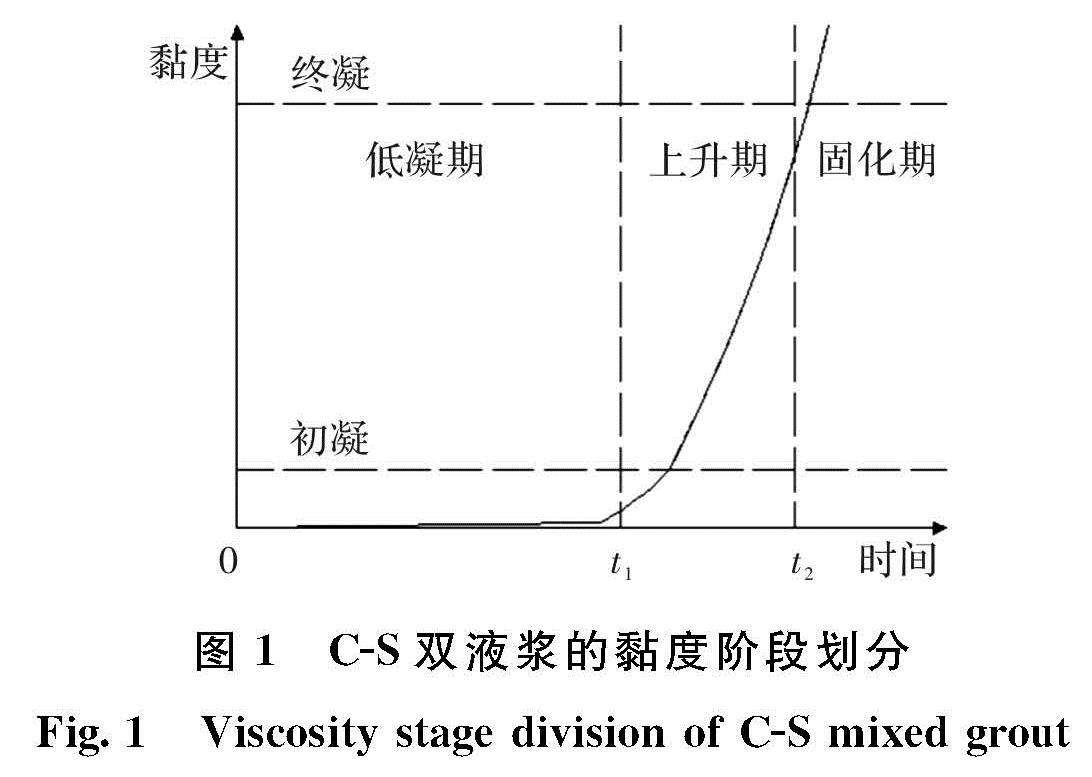
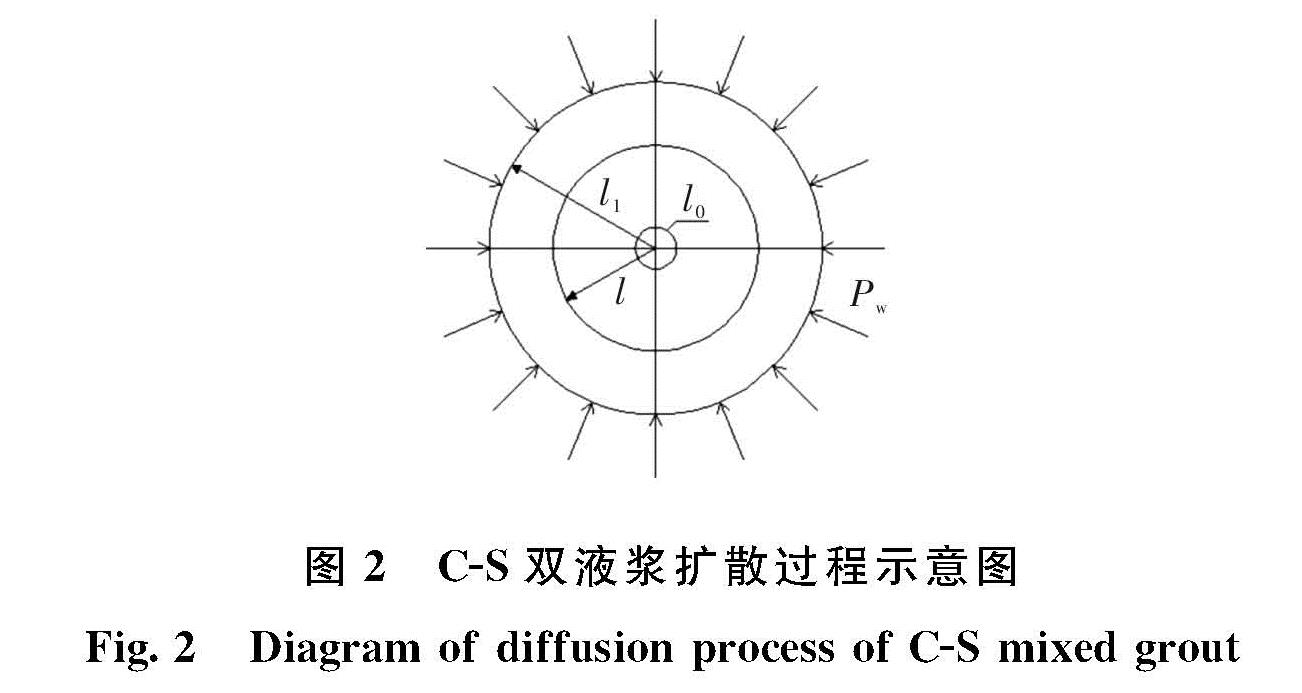
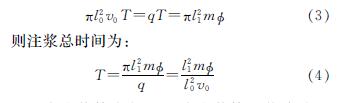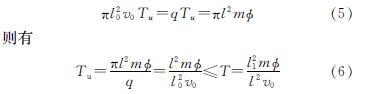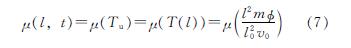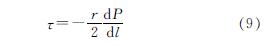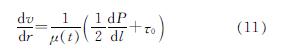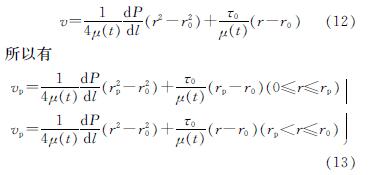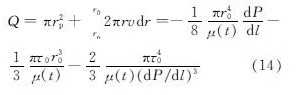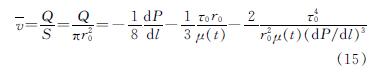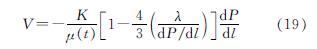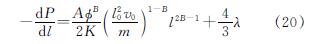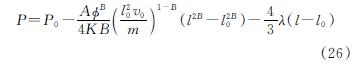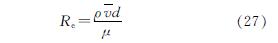1.3.1 双液浆黏度变化时间与扩散半径的关系
根据T时间内浆液在地层中渗透扩散的量与注浆管注浆量相等,可得到:
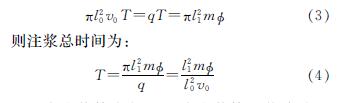
式中:l0为注浆管半径; v0为注浆管内浆液的流速; q为注浆管的流量; m为浆液柱形扩散的高度; φ为受注地层的孔隙度.
图3 浆液柱形扩散理论模型
Fig.3 Theoretical model of grout cylindrical diffusion
由1.1.2节可知:t(t≤T)时刻注入地层中的浆液质点,其最终扩散至半径l处.令Tu=T-t,则从t时刻至注浆结束时刻,即Tu时间段内,注入地层中的浆液量为
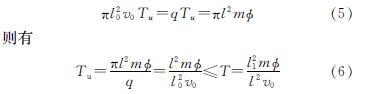
由于注浆管内浆液的速率不变,因此对地层中某一确定的浆液扩散半径l,浆液质点由注浆孔处到达该位置所需要的时间是固定不变的,而浆液质点由注浆孔处到达该位置所需要的时间也就是浆液的黏度增长时间Tu,即对扩散半径l处的浆液质点而言,其黏度增长时间是固定不变的[22].由此可知:浆液质点的黏度增长时间与浆液的扩散半径l一一对应,即Tu=T(l),所以有
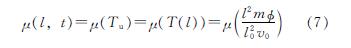
1.3.2 双液浆的渗流运动方程
假定受注地层为由直径相同的毛细管排列而成的多孔介质,即符合均匀毛管组模型,双液浆的渗流等效为浆液质点在所有毛细管道中流动的叠加[23].设毛细管半径为r0,在毛细管中取一段与管轴同轴的流体柱微元素,流体柱半径为r(r≤r0),长度为dl,流体柱的左右两端分别作用压力P和P+dP,两侧的压力差为dP,流体柱的表面上所受剪切应力为τ,其方向向左,与浆液的流动方向相反,浆液在毛细管道中的流动情况如图4所示.
由流体柱微元素的受力平衡条件可得到:
Pπr2-πr2(P+dP)-2πrτdl=0 (8)
化简得到浆液的剪切应力为
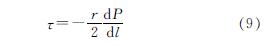
图4 浆液在毛细管道中的流动示意图
Fig.4 Flow diagram of grout in capillary pipe
当剪切应力τ≤τ0时,浆液不发生相对运动,呈活塞式运动; 当剪切应力τ>τ0时,浆液发生相对运动.结合图4可知,毛细管中浆液的速度分布为截头抛物面形状.令τ=τ0,可得到浆液活塞式运动的半径为

由此可以说明当0≤r≤rp时,浆液的剪切应力τ为0,当rp<r≤r0时,浆液质点所受剪切应力与该质点到管轴的距离r成正比,如图5所示.
图5 浆液剪应力分布示意图
Fig.5 Diagram of shear stress distribution in grout
将式(9)代入双液浆的流变方程式(2),可得到:
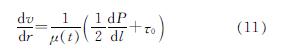
对式(11)采用分离变量法积分,代入壁面无滑移条件r=r0,v=0,可得到浆液的速度方程为
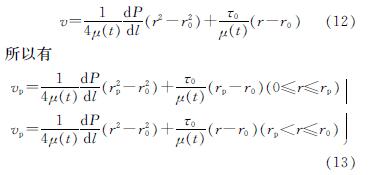
毛细管道中浆液的总流量Q为活塞运动区与相对运动区两部分的流量之和,即
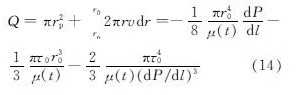
则浆液在毛细管中的平均流速为
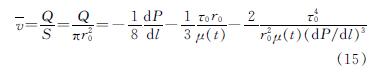
浆液需要克服阻碍其流动的屈服剪切力τ0,即达到浆液的启动压力梯度λ,才能保证浆液能在毛细管中顺利流动.令Q=0,可解得:
-(dP)/(dl)=(2τ0)/(r0)=λ (16)
由Dupuit-Forchheimer公式可知,被注介质内任意一点的渗流速度V与该点处浆液的平均速度v^-及被注介质孔隙度φ满足如下关系:
V=φv^- (17)
被注介质渗透率K与毛细管半径r0满足如下关系:
K=(φr20)/8 (18)
由于注浆开始后其压力梯度-dP/dl?启动压力梯度λ,忽略高阶微量并结合式(17)可得到:
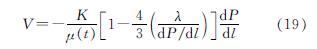
根据注浆过程中注浆管流量与扩散断面处流量相等,即πl20v0=2πlmV,并将表征双液浆黏度时空效应的表达式(7)代入,可得到:
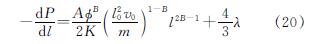
采用分离变量法对式(20)进行积分可得到:

式中:C为积分常数.
代入注浆边界条件:

式中:P0为注浆孔处的注浆压力; Pw为注浆点处的地下水压力.
令ΔP=P0-Pw,由式(21)和(22)可得到:

由此可得浆液的扩散半径表达式为

根据浆液扩散半径l处的浆液压力为P,同时结合注浆边界条件,对式(20)进行积分,得

可得到浆液压力的表达式为
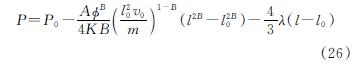
1.4 参数确定方法与公式适用范围
1.4.1 参数确定方法
由以上公式推导的过程可以看出,与双液浆柱形渗透扩散过程相关的参数有:初始扩散半径l0,双液浆的屈服剪切力τ0,注浆点处的地下水压力Pw,注浆压力P0,毛细管半径r0,双液浆黏度参数A和B,受注地层孔隙度φ,浆液柱形扩散的高度m,受注地层渗透率φ,注浆管内浆液的流速v0.
l0为注浆管半径,可以通过多次测量求平均值获得; 屈服剪切力τ0采用旋转黏度计或毛细管黏度计测定得到; 地下水压力Pw由公式Pw=ρgh计算得到(ρ为水的密度,h为注浆段的埋深); 注浆压力P0采用在注浆孔附近安装压力表,由现场测试数据得到; 渗透率K由公式K'=Kρg/μw计算得到[24](K'为渗透系数,μw为水的黏度); 孔隙度φ可在室内或现场测定得到; 在已知K和φ的前提下可由式(18)计算出毛细管半径r0; 黏度参数A和B可由室内浆液特性试验得出相关数据后拟合得到; 柱形扩散的高度m可根据工程设计要求获得; 浆液的流速v0可由现场实测得到.
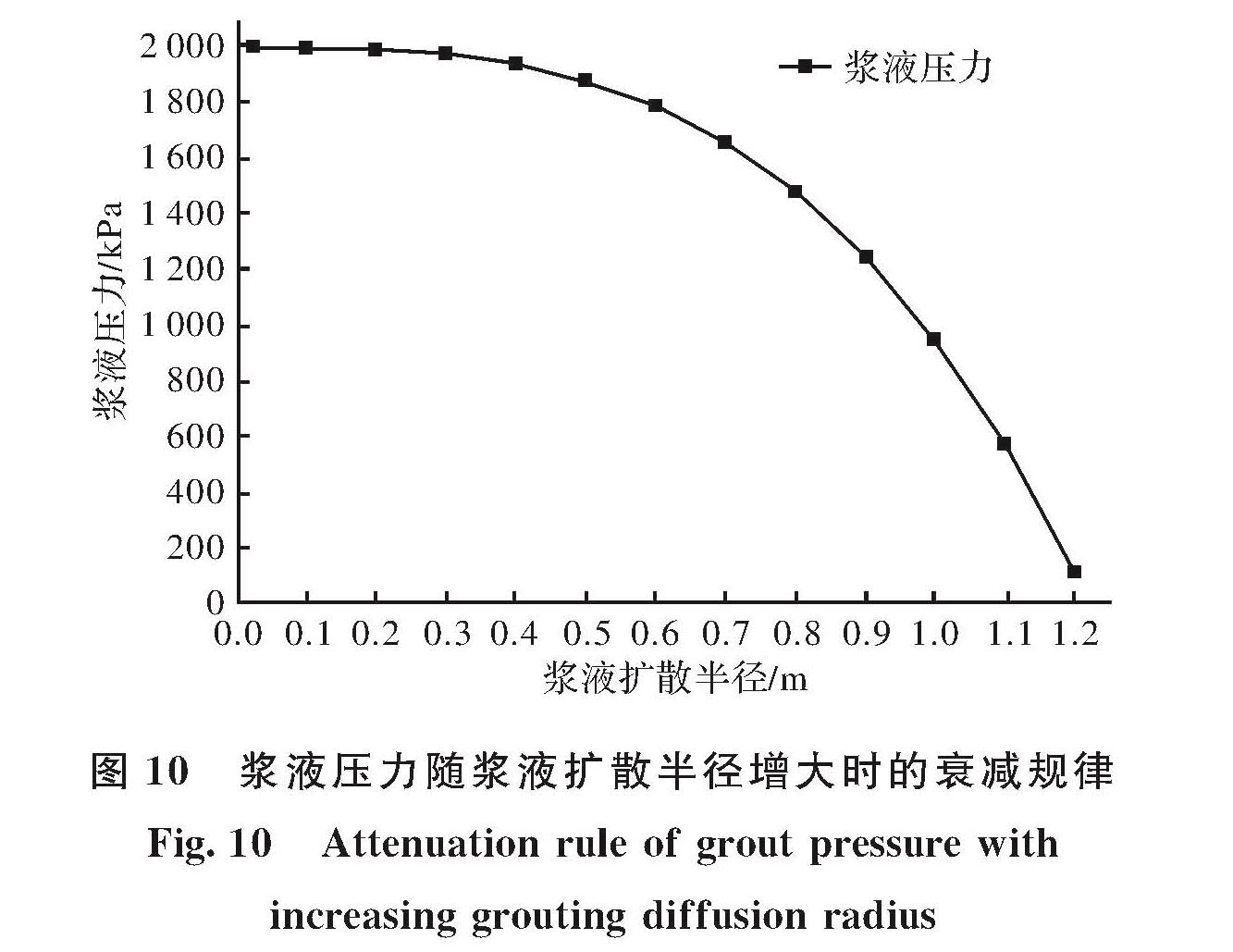
至此,对于考虑黏度时空效应时C-S双液浆柱形渗透注浆的扩散半径计算式(24),除了浆液扩散半径l1一个未知参数外,其他参数均可通过上述方法得到; 反之,已知浆液扩散半径l1,可以由式(23)求出理论上的压力差ΔP.在求得浆液扩散半径l1后,由式(26)可以得出浆液扩散范围内浆液压力的衰减规律.
1.4.2 公式适用范围
以上公式均是在假定浆液流态为层流的情况下推导出来的,当浆液流态为紊流时,上述公式不再适用.张伟[25-26]等的研究表明:当雷诺数Re<2 000时浆液为层流流态,当2 000≤Re≤4 000时浆液为层流与紊流的混合流态,当4 000<Re时浆液为紊流流态.
雷诺数的计算式为
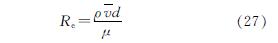
式中:ρ为浆液的密度; v^-为浆液的平均流速; d为一特征长度(浆液流过圆形管道时,d为圆管的当量直径); μ为浆液的动力黏度.