基金项目:国家自然科学基金项目(No.51779183)
第一作者:陈俊博(1979-),女,工学硕士,讲师,从事建筑工程施工管理和建筑工程施工技术研究.E-mail: t319796173@126.com
(1.郑州信息科技职业学院 基建处,河南 郑州 450046; 2.武汉大学 水资源与水电工程科学国家重点实验室,湖北 武汉4300722)
(1.Zhengzhou Vocational University of Information and Technology, Zhengzhou 450046,China; 2.State Key Laboratory of Water Resources and Hydropower Engineering Science,Wuhan University,Wuhan 430072,China)
drainage pipe pile, consolidation, pore pressure, consolidation degree, opening ratio
DOI: 10.15986/j.1006-7930.2021.05.004
复合地基是一种有效的软土地基处理手段,其中预制刚性桩在沉桩过程中由于挤土效应,会在桩周土体内产生不可忽视的超静孔隙水压力,若此超孔隙水压力不能及时排出,可能会造成土体的抗剪强度降低、邻桩的上浮或偏移、降低桩基承载力等有害影响[1-6].为探究沉桩后桩周土体的孔压分布情况以及消散规律,Randolph等[7,8]基于圆孔扩张理论,先后应用理想弹塑性模型和修正剑桥模型推导出沉桩后桩周土体内的初始孔压分布情况,并根据径向固结理论求解得出超孔压的消散解答.之后,通过考虑不同的土体特性以及桩周土体的扰动特性等因素,许多学者[9-14]针对沉桩后桩周土的固结特性展开了大量研究.
随着桩基础使用的日益频繁,加快沉桩后桩周土体内由于挤土效应引起的超孔压的消散成为该领域一个重要问题.针对此问题,工程中常采用刚性桩与具有透水性的散体桩以及排水竖井联合使用,用于加速沉桩后超孔隙水压力的排出[15-19],以加快地基承载力的发挥.近年,一种排水管桩的概念逐步被工程界熟知,其集排水和承载于一体,是软基处理的一种新方法.史美东等[20]提出一种砂衬混凝土桩,并通过实例分析了这种桩型在提高承载力方面具有明显优势.周小鹏和梅国雄[21]提出一种桩身设有排水孔的主动式排水静压管桩,并对其进行了有限元模拟.基于此,黄勇等[22-23]先后开展了室内模型试验,分别探究了单桩和群桩的孔压消散规律.Ni等[24-25]也对这种排水管桩开展了系列研究,总结得出排水管桩的压缩特性和加固效果.唐晓武等[26]提出一种能排水并增大摩阻力的预制管桩,并推导得出相应复合地基在加载后的固结解析解.以上关于排水管桩的研究,多是从数值模拟和室内模型试验两方面开展,而关于沉桩后到施加上部荷载之前这段时间内,桩周土体的消散解析解方面的研究却鲜有报道.
本文结合排水管桩的特点,采用半透水边界条件模拟桩-土界面的边界排水特性,基于径向固结理论,针对沉桩后桩周土体的排水固结进行解答.并根据所得解答,对沉桩后桩周土体内的超孔隙水压力的消散特性进行分析.
图1为排水管桩地基固结示意图,ra为管桩内半径,rb为管桩外半径,rp为由于沉桩引起的塑性区半径,re为单桩排水影响区域半径,本文用半透水边界模拟桩-土界面的透水特性.
相对于整个桩体而言,桩体上设置的径向排水通道可以视为一微小圆管,半径为R.根据Hagen-Poiseuille定律,可假设微小圆管横截面上的流速vw(r)呈抛物线分布,管流的水力梯度为i,如图2所示.
根据能量守恒原理,可得到管内平均流速为
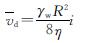 (1)
(1)
式中:R为排水通道的半径,η为孔隙水的动力粘滞系数.
若设桩体的平均径向渗流流速为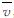 ,桩体的外表面积为S,排水孔在桩身开口的总面积为Sd.由于单位时间内通过桩体的总流量等于通过排水孔的总流量,即
,桩体的外表面积为S,排水孔在桩身开口的总面积为Sd.由于单位时间内通过桩体的总流量等于通过排水孔的总流量,即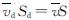 ,故可得到桩体的平均渗流流速为
,故可得到桩体的平均渗流流速为
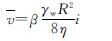 (2)
(2)
其中,β=(Sd)/S,定义为排水桩的开孔率.
若将桩体等效为渗透系数为kp的透水介质,结合达西定律即可得到桩体的等效渗透系数为
kp=(βγwR2)/(8η) (3)
在排水孔沿桩体纵向等间距均匀布置的情况下,纵向布孔间距为d,布孔列数为nd,排水孔半径为R,则对应的开孔率可表示为
β=(ndR2)/((ra+rb)d) (4)
基本假设:
(1)仅考虑径向渗流,且满足达西定律;
(2)沉桩后土体固结看作是土骨架的弹性位移过程,且总应力保持不变;
(3)假设排水管桩的排水孔在打设过程中处于关闭状态,打设完成后打开.
根据平面应变问题的弹性应力应变关系得
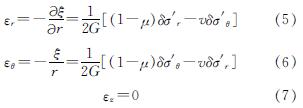
式中:ξ为桩周土中任意一点的位移,以桩外侧为正; G为土体的剪切模量; μ为土体的泊松比; εr、εθ和εz分别为土体的径向、环向和竖向的应变; δσ'r、δσ'θ分别为土体径向和环向的有效应力变化量.
土体的体积应变为
εv=εr+εθ+εz (8)
根据有效应力原理,可得土体中总应力的变化量为
δσr=δσ'r+u (8)
δσθ=δσ'θ+u (9)
土体径向平衡条件:
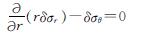 (10)
(10)
综上,可得
εv=-(1-2μ)/(2(1-μ)G)u(11)
由渗流连续性可得
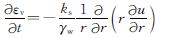 (12)
(12)
所以,可得到沉桩后桩周土体的固结控制方程:
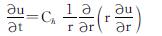 (13)
(13)
其中,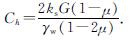
假设在沉桩过程中,土体发生的是不排水剪切,且服从Tresca屈服准则.根据经典的圆柱形扩张理论,并结合Henkel孔压公式可得出沉桩后桩周土体的超孔隙水压力的初始分布为[7]
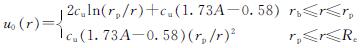 (14)
(14)
其中,rp=rb(G/cu)1/2.
式中:cu为不排水剪切强度; G为剪切模量; rp和Re分别为沉桩所引起的塑性区和影响区的半径; A为Skempton孔压系数.
目前,在单桩桩周土体的固结计算中,都假设了r=Re处的外边界孔压始终为零,即外边界为完全排水边界.根据初始条件可以看出,在距离桩体较远处的位置,由沉桩引起的初始孔压趋近于零,桩周土体内具有两条水平排水路径(分别向内或者向外).所以,对于单桩而言,将外边界视为完全排水边界是合理的.但对于群桩而言(如图3所示),在邻桩的排水影响下,桩周土体内的空隙水仅能通过桩体排出,根据排水的对称性可将外边界视为不排水边界.
根据以上分析,在如图所示的布桩形式下,单桩沉桩的影响区域的半径为Re,其排水区域的等效半径为re.当re小于Re时,桩周土体固结计算模型中的外边界条件为
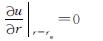 (15)
(15)
其中,根据面积等效原理,桩距为D,等效半径为
re=(D)/(π1/2) (16)
当re大于Re时,桩周土体的外边界条件可视为
u(Re)=0 (17)
其中,Re可取5~10rp [7],本文将初始孔压为1 kPa的位置视为完全排水边界,根据初始条件可得
Re=rb(G(1.73A-0.58))1/2 (18)
对于刚性桩体而言,在排水过程中桩体的体积不发生变化,应变为零,则
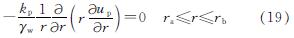
其中,kp为桩体的等效径向渗透系数,up为桩体内的孔压.
由于透水桩体内部设置的竖向排水通道无填充,且与地面大气相通,故可将其中的超孔隙水压力视为恒为零,即
up(ra)=0 (20)
结合以上两式,积分可得
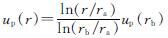 (21)
(21)
在桩-土界面处(r=rb),由渗流连续性可得
up(rb)=u(rb) (22)
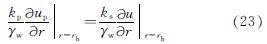
式中:ks为桩周土体的径向渗透系数.
进一步,整理可得出桩-土界面处的边界条件:
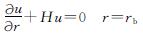 (24)
(24)
其中,H=-(kp)/(ksrbln(rb/ra)).
采用分离变量法,令
u(r,t)=w(r)T(t) (25)
则
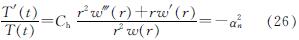
令λn=(α2n)/(Ch),进而得
T'(t)=Chλ2nT(t)=0 (27)
r2w″(r)+rw'(r)+λ2nr2w(r)=0 (28)
由此,可得
Tn(t)=Cne-Chλ2nt (29)
wn(r)=AnJ0(λnr)+BnY0(λnr) (30)
当re小于Re时,将式(30)代入外边界条件(式(15))中得
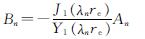 (31)
(31)
若令
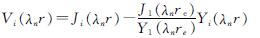 (32)
(32)
当re大于Re时,外边界为完全排水边界条件,将式(30)代入外边界条件(式(17))中得
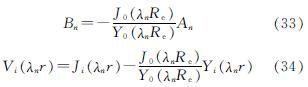
则
wn(r)=AnV0(λnr) (35)
将桩-土界面(r=rb)处的半透水边界条件得
λnV1(λnrb)-HV0(λnrb)=0 (36)
通过此方程(式(36)),可解得对应的本征值λn,且有无数解.
综上,可得
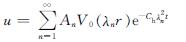 (37)
(37)
由此,初始时刻桩周土内孔压为
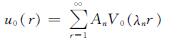 (38)
(38)
由于Bessel函数系{V0(λnr)}在[0, rb]和[0, re]上满足带权重r的正交性,可得
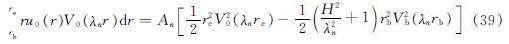
将初始条件(式(14))以及求得的本征值λn代入上式中可得到相应的An,从而可计算出沉桩后桩周土体在任意位置、任意时刻的超孔隙水压力,通过MATLAB编程实现计算.
定义桩周土体任意位置处的固结度为
Ur=1-(u(r,t))/(u0(r)) (40)
为研究桩周土体的总体固结情况,定义土体的固结度U(t)为
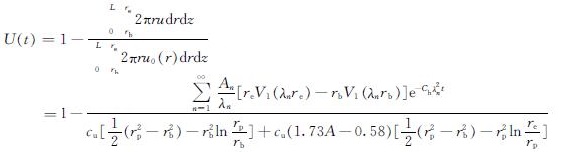 (41)
(41)
根据上文解答,探究沉桩后桩周土体内的孔隙水压力消散特性,土体基准参数和透水管桩的基准参数分别如表1和表2所示.在下文的参数分析过程中,改变所分析参数的值,其余参数保持基准取值不变.
通过由本文所得解答计算的初始孔压(式(38))与由小孔扩张理论中所得的初始条件(式(14))中的初始孔压进行对比,以验证级数项数N取到一定值时,本文解答的计算结果能够值收敛.如图4所示,当级数项数取不同值时,计算所得初始孔压分布曲线的波动程度不同.当N=10时,计算的初始孔压分布曲线波动十分明显,随着级数项项数逐渐增大,波动逐渐集中在桩壁附近,并且桩壁孔压与初始条件逐渐接近.可以看出,当N取104时,计算所得初始孔压与初始条件给出的初始孔压基本吻合,当N取103时,仅在桩壁处存在微小波动.所以,在计算桩周土体孔压时,当r>1.5rb时,级数项项数取到103左右即可.
图5为不同级数项数N下的平均固结度曲线,从中可以看出,当级数项数取1时,计算所得固结度偏小,当级数项项数取10以上,计算所得平均固结度曲线完全重合.因此,在计算平均固结度时,级数项项数取到10即可.
图4 不同级数项数下的初始孔压分布
Fig.4 Distribution of the initial excess pore-water pressure for different numbers of the series term
如图6所示,沉桩后某一时刻桩周土体内的孔压沿着径向呈现出先增后减的趋势.随着固结时间的增长,平均孔压逐渐减小.同时,在离桩体较远处,随着固结时间的增长,孔压较初始值先增大再减小.这是由于土体内的孔压在初始时刻就存在沿径向的梯度,开始排水后,离桩体较远处的孔隙水压力先进行平衡(从低压处向高压处流动),然后再向排水边界流动.图7为沉桩后桩周土内不同位置的固结度曲线,从其中可看出,在距离桩体较远处的固结度出现负值,说明此处的孔压会大于初始值,而在距离桩体较近处,这种现象较不明显.进一步分析可得,由于沉桩后的初始孔压分布存在一定梯度,且桩壁处的孔压最大,沿着径向逐渐减小,所以造成沉桩后桩周土体内的渗流路径是:距桩体较近处的超孔隙水直接沿着排水桩排出,而距离桩体较远处的超孔隙水先流向弹性低压区,再转头流向排水桩排出.
图8表示不同开口率下的平均固结度曲线,从中可看出,随着开孔率β的增加,固结度的增长变快,孔压的消散变快.当β超过10-7时,继续增大其值,固结度曲线的变化很小,说明此时增大开孔率对加快孔压消散的效果不明显.
图9为不同桩距下的固结度曲线,其中当re小于Re时,桩周土的外边界是不排水边界,桩距分别取3 m、4 m、5 m、6 m,可以看出,随着桩距的增大,桩周土的平均固结度减小.当桩距继续增大到re等于Re时,桩周土的外边界可视为完全排水边界,桩周土体的固结度的增长先减慢后加快,平均固结度发展速率位于D=4 m和D=5 m两种情况之间.
本文针对排水管桩沉桩后桩周土体的固结问题进行解答,推导出相应的孔压和固结度解析解,并验证了解答的收敛性.基于所得解答,通过参数分析,探究了沉桩后排水管桩桩周土体的固结特性.总结得出以下结论:
(1)排水管桩沉桩后桩周土体内的孔隙水排水路径与普通管桩的不同,距桩体较近处的超孔隙水直接沿着排水桩排出,而距离桩体较远处的超孔隙水先流向弹性低压区,再转头流向排水桩排出;
(2)随着开孔率β的增加,孔压的消散变快.当β超过10-7时,继续增大其值对加快孔压消散的效果不明显;
(3)当re小于Re时,随着桩距的增大,桩周土的平均固结度减小.当桩距继续增大到re等于Re时,桩周土体固结度的增长先减慢后加快.