(1.国网甘肃省电力公司 建设分公司,甘肃 兰州,730050; 2.西安建筑科技大学 土木工程学院,陕西 西安,710055)
(1.State Grid Gansu Power Construction Company, Lanzhou 730050, China; 2.School of Civil Engineering, Xi'an Univ.of Arch.& Tech., Xi'an 710055, China)
CFST; latticed angles; stiffeners; axial tension test; bearing capacity; rigidity
DOI: 10.15986/j.1006-7930.2021.05.010
钢管混凝土构件充分利用了混凝土对钢管的支撑作用以及钢管对混凝土的约束作用,从而具有优良的受压性能,被广泛应用于工程实践[1-6].而钢管混凝土用作输电杆塔、钢管混凝土桁架桥的下弦杆时,拉力会对钢管混凝土构件的破坏起控制作用.因此,对钢管混凝土构件受拉性能开展研究具有重要意义.
以往主要针对普通钢管混凝土构件的受拉性能开展研究.潘友光等[7]对普通圆钢管混凝土构件进行了轴拉试验,结果表明:内部混凝土的存在可使钢管的受拉纵向屈服应力提高约10%.张素梅等[8]通过有限元分析,得出钢管混凝土构件受拉承载能力较空钢管最大提高15%.蔡文哲等[9]对10个钢管混凝土柱在轴向拉力作用下的受力行为进行了数值模拟.结果表明:钢管混凝土轴向受拉时,拉力主要由钢管承担,混凝土的主要作用是对钢管的径向收缩起支撑作用.Han等[10]对18个钢管混凝土试件进行了轴拉试验,研究了含钢率、混凝土强度、钢管与混凝土粘结力等因素对构件轴拉性能的影响,提出了轴拉承载力计算公式.Li等[11]对钢管混凝土构件的拉弯性能展开了试验研究和有限元分析,结果表明:钢管与混凝土能很好地协同工作,提高构件的承载能力,极限荷载时,构件表现出良好的塑性.Zhou等[12]对不同尺寸的圆钢管混凝土构件和空钢管进行了轴拉试验,研究其承载力和刚度差异,结果表明:与空钢管相比,钢管混凝土构件的承载力提高10.2%,刚度提高28.7%.
钢管混凝土构件受拉时,外荷载主要由钢管承担.当外荷载较大时,增大钢管壁厚可能会造成钢管难以加工、强度降低、层状撕裂等问题,因此,在钢管混凝土内配置加劲件成为提高钢管混凝土构件受拉承载能力的重要途径.陈驹[13]、王军等[14]对内配钢筋的钢管混凝土构件和内配角钢的钢管混凝土构件开展了轴拉试验研究,提出了相应的承载力和刚度计算公式.Xu等[15]采用试验和有限元分析相结合的方法,研究了内配角钢钢管混凝土构件的传力机理.结果表明:内配角钢与外钢管在无任何连接情况下仍能达到受拉屈服.
综上所述,国内外学者对钢管混凝土受拉性能的研究主要集中于未加劲的普通钢管混凝土构件,对内配加劲件的钢管混凝土构件受拉性能研究较少.本文针对内配钢骨和加劲肋的圆钢管混凝土构件进行轴拉试验和有限元模拟分析,研究其受力过程、破坏机理、承载力及刚度.将按照国内外规范计算的试验试件受拉承载力和刚度计算结果与试验结果进行对比,探究现有规范对内配钢骨及加劲肋圆钢管混凝土构件受拉承载力和刚度的适用性.
为研究内配钢骨和加劲肋圆钢管混凝土构件的轴拉力学性能,设计了7个轴拉试件,试件设计参数和试件图分别如表1、图1所示.钢管由两块钢板卷制焊接而成,外径均为400 mm,长度为3 000 mm,壁厚为6 mm.内配纵肋焊接在钢管内壁,其截面尺寸为4-4 mm×24 mm.由于钢管内部无法施焊,故内配钢骨仅一端与端板焊接,钢骨截面尺寸为4-L40 mm×4 mm.环肋焊接在钢管内壁,与纵肋相交处断开纵肋,其截面尺寸为5 mm×24 mm.为固定钢骨位置,在角钢上下端100 mm处设置长度为50 mm的拉结筋,分别与角钢及钢管点焊.为了保证受拉过程中试件端板与钢管之间可靠传力,在试件两端焊接16块加劲板.试件两端端板采用高强螺栓与加载装置连接.
表1 试件主要参数
Tab.1 Main parameters of specimens
图1 钢管混凝土试件
Fig.1 CFST specimens
试件除角钢采用Q235B钢材外,其余钢材均采用Q345B; 混凝土强度等级为C50.钢材的材性试验结果见表2.混凝土28 d实测立方体抗压强度标准值为52.07 MPa,弹性模量为34 250 MPa.
表2 钢材材性试验结果
Tab.2 Material properties of steel
采用8 000 kN电液伺服实验机对试件进行加载,试件下端与底座固接,上端通过刚性法兰与作动器连接.试验装置如图2所示.试验采用分级加载.先预加载至承载力设计值的10%,再卸载到0%,检查试验装置、测试仪器是否正常工作.正式加载时,在承载力设计值的60%之前,每一级荷载增量取设计值的10%; 当荷载达到设计值的60%后,荷载增量取设计值的5%; 当荷载接近设计值时,缓慢持续加载.轴拉试件以跨中应变达到5 000×10-6时对应的荷载作为试件的极限荷载[10].为避免试件断裂对试验系统的不利影响,当试件跨中应变超过5 000×10-6后停止加载.
图2 试验装置
Fig.2 Test setup
试件位移计与应变片布置如图3所示.在试件下端板布置4个位移计以测量试件的纵向位移,编号分别为W1～W4.在试件中部前后对称布置2个位移计以测量试件的颈缩变形,编号分别为W5、W6.在距试件两端500 mm处均匀布置8个纵向应变片,试件跨中均匀布置8个纵向应变片和4个环向应变片,以监测试件的纵向和环向应变,用“L”和“H”分别表示纵向和环向,应变以拉为正、压为负.
图3 测点布置
Fig.3 Arrangement of measurement points
各试件试验现象基本一致.加载过程中,试件的轴向和颈缩变形不明显.各试件的变形形态如图4所示.通过测量加载前后试件的长度和截面周长变化,可得到试件的轴向和环向变形,测量结果如表3所示.由表3可知,各试件近加载端的颈缩变形最大.
图4 试件变形
Fig.4 Deformation of specimens
表3 试件伸长量与颈缩量(单位:mm)
Tab.3 Elongation and necking shrinkage of specimens/mm
为观察试件内部混凝土的开裂情况,试验后将试件外钢管割开,得到各试件内部混凝土的裂缝分布情况,如图5所示.ZL-1试件内部混凝土开裂,表明外荷载能通过钢管与混凝土之间的相互作用传递至内部混凝土.与ZL-1试件相比,ZL-2试件由于环肋的存在,环肋两侧的混凝土裂缝更密集,最大裂缝宽度出现在相邻环肋之间,表明环肋能更均匀地将外荷载传递至内部混凝土,使混凝土均匀受力.ZL-3试件的混凝土裂缝宽度和间距均小于ZL-2试件,表明内配钢骨有效参与了试件的受拉作用并抑制了混凝土裂缝的发展.与ZL-2试件相比,ZL-4和ZL-5试件的混凝土裂缝密而窄,表明内配件参与了试件的受拉作用并抑制了混凝土的开裂.ZL-6和ZL-7试件由于环肋间距较大,内部混凝土裂缝的发展与普通钢管混凝土试件ZL-1相似.
图5 试件内部混凝土裂缝形态
Fig.5 Crack patterns of concrete in specimens
各试件的荷载-位移曲线如图6所示.由图可知,各试件的荷载-位移曲线都包括明显的弹性阶段、弹塑性阶段及塑性阶段.加载初期,试件整体处于弹性状态,荷载与位移呈线性关系; 随着荷载增加,试件进入弹塑性阶段,试件受拉刚度明显降低; 塑性发展阶段,荷载仍保持缓慢增加.
各试件的受拉承载力如表4所示.由表4可知,环肋对试件的受拉承载力影响较小,因此,可取ZL-1、ZL-2、ZL-6及ZL-7试件的受拉承载力平均值3 446 kN作为该含钢率普通钢管混凝土构件的受拉承载力.由ZL-3、ZL-4及ZL-5试件受拉承载力与该值对比可知,内配钢骨使试件受拉承载力提高471.3 kN,提高幅度为13.60%.试件内配4-L40×4的钢骨屈服荷载367.9 kN<471.3 kN,表明内配钢骨能很好地参与试件的受拉作用并达到受拉屈服.加劲纵肋使试件受拉承载力提高269.47 kN,提高幅度为7.82%; 同时内配钢骨和加劲纵肋使试件受拉承载力提高790.56 kN,提高幅度为22.94%.
图6 各试件荷载-位移曲线
Fig.6 Load-displacement curves of specimens
表4 试件受拉承载力试验值
Tab.4 Test values of ultimate tensile bearing capacity of specimens
各试件中部荷载-平均纵向应变曲线如图7所示.由图可知,各试件应变发展趋势基本一致.加载初期,应变呈线性增长,试件处于弹性状态; 随着荷载增加,纵向变形速率加快,呈现出非线性特征,试件开始屈服,应变快速增大.与普通钢管混凝土试件相比,内配纵向加劲肋和钢骨小幅提高了试件的刚度.
图7 试件中部荷载-平均纵向应变曲线
Fig.7 Load-average longitudinal strain curves in the middle of each specimen
图8为各试件中部荷载-平均环向应变曲线.由图可知,加载过程中,钢管环向应变较小.当试件达到受拉极限荷载时,各试件钢管横向应变均未达到屈服应变,其原因为核心混凝土抑制了钢管的颈缩变形.
图8 试件中部荷载-平均环向应变曲线
Fig.8 Load-average hoop strain curves in the middle of each specimen
采用有限元软件ABAQUS对试件进行数值模拟.钢材本构关系采用韩林海等[16]提出的五折线本构模型.采用ABAQUS中的非耦合型延性损伤准则[17]模拟钢材刚度退化和破坏现象,参考Wierzbicki[18-19]和Xue[20]提出的金属材料损伤理论.Yu[21]将钢材的等效塑性损伤应变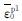
与应力三轴度η的关系简化为
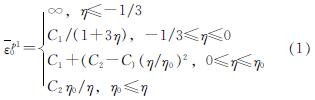
其中:C2=-ln(1-AR); C1=C2(31/2/2)1/n; σ=K(ε)n.
式中:C1为钢材平板纯剪切状态下(η=0)等效塑性损伤应变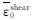
; C2为单轴拉伸时(η=η0)的等效塑性损伤应变
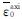; η0为常数,取1/3; K、n为钢材硬化参数,由钢材拉伸试验真实应力-应变曲线拟合得到.
损伤后的应力下降路径如图9所示.图中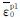
为钢材进入损伤时的等效塑性应变,
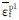为钢材最终失效时的等效塑性应变.钢材达到峰值应力后的下降路径可以表示为剩余应力形式,即:σ=(1-D)
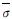,D为强度和刚度退化损伤因子,当D=0时,钢材进入初始损伤; D=1时,钢材完全破坏,失效单元删除.
图9 钢材损伤下降路径
Fig.9 Steel damage descent path
混凝土采用韩林海等[16]提出的塑性损伤模型,该模型可有效模拟多轴应力状态下混凝土的塑性性能.混凝弹性模量取试验值,泊松比取0.2[16].塑性模型中的膨胀角ψ取30°,双轴受压强度与单轴受压强度之比fb0/fc0取1.16,拉、压子午线偏量第二应力不变量的比值Kc取0.666 7,黏性系数μ取0.000 25[22].对于混凝土的受拉本构关系,采用能量破坏准则考虑混凝土受拉软化性能更具有收敛性[23],其主要参数包括混凝土的断裂能和开裂应力.对于断裂能的计算采用CEB-FIP MC90[24]中提供的计算公式,对于开裂应力参考沈聚敏[23]给出的混凝土抗拉强度计算公式.
各部件均选用8节点减缩积分实体单元(C3D8R).钢管、加劲肋及加载板之间采用绑定连接; 钢管和混凝土之间的相互作用采用接触模拟,法向为硬接触,切向为法摩擦,摩擦系数取0.60[25].模型一端固定,另一端约束除轴向位移外的所有自由度并施加位移荷载.试件有限元模型如图 10所示.
图 10 有限元模型
Fig.10 Finite element model
有限元分析的荷载-位移曲线与试验结果对比如图 12所示.由图可知,有限元与试验荷载-位移曲线吻合较好,表明有限元模型能较为准确地模拟内配钢骨及加劲肋圆钢管混凝土构件的轴拉承载性能.
图 11 试件有限元分析破坏形态
Fig.11 Failure patterns of finite element analysis of specimens
图 12 有限元与试验荷载-位移曲线对比
Fig.12 Comparison of load-displacement curves between FEM and test
试件的有限元模拟承载力与试验结果对比如表5所示.由表可知,NF/Nu平均值为1.016 2,最大偏差为2.78%,二者吻合较好.
表5 有限元模拟结果与试验结果对比
Tab.5 Comparison of bearing capacity between finite element analysis and test results
图 13给出了内配钢骨及加劲肋圆钢管混凝土构件各部件有限元模拟的应力发展过程.构件应力发展过程为:混凝土开裂→钢骨屈服→钢管屈服→构件破坏.构件达到极限受拉荷载时,内配钢骨受拉屈服,表明内配钢骨能有效地参与受拉作用.内配钢骨是提高构件受拉承载力的有效方式.
图 13 试件应力发展过程
Fig.13 Stress development process of specimen
图 14给出了内配钢骨圆钢管混凝土构件及各部件的荷载-应变曲线.由图可知,试件的荷载-应变曲线包括以下四个阶段:
图 14 ZL-3试件及其组成部件的荷载-应变曲线
Fig.14 Load-strain curves of ZL-3 specimen and its components
(1)OA段:试件整体和各组件均保持弹性状态,直到A点,核心混凝土出现裂缝,内力发生重分布.在此之前,混凝土与钢骨变形一致.由于内配角钢的轴向刚度小于混凝土的轴向刚度,因此,此时内配钢骨承担外荷载的比例小于混凝土承担的比例.A点时,钢管、混凝土和钢骨承担外荷载比例分别为54.14%、38.58%和7.28%.
(2)AB段:外荷载保持线性增加.由于混凝土开裂导致构件的组合刚度下降,同时内力发生重分布,混凝土承担的外荷载比例明显下降,内配角钢承担的外荷载比例有所增加.由于内配角钢强度低于钢管强度,内配钢骨比外钢管先达到受拉屈服.B点时,外钢管屈服,此时,钢管、混凝土和钢骨承担外荷载比例分别为87.25%、2.07%和10.68%.
(3)BC段:钢材屈服后进入强化阶段,荷载呈非线性增长.以跨中应变达到5 000×10-6(C点)所对应的荷载作为试件的极限荷载,此时试件已完全屈服,钢管、混凝土和钢骨承担外荷载比例分别为89.09%、0.39%和10.52%.混凝土承担的外荷载很小,可认为混凝土对构件极限受拉承载力无影响.
(4)CD段:此阶段外荷载几乎保持不变,曲线未出现下降段,D点的应变大于10 000×10-6,构件表现出良好的塑性.
《特殊钢管混凝土构件设计规程》(CECS 408: 2015)[26]给出了内配非约束型加劲件的钢管混凝土构件受拉承载力计算公式,该公式不仅考虑了内部混凝土对钢管的支撑作用,同时也考虑了加劲件对钢管混凝土构件承载力的提高.具体公式如下:
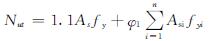(2)
对于外钢管设置纵向加劲肋的构造形式,可将钢管与纵肋视为整体,内部混凝土主要约束钢管的颈缩变形从而提高构件受拉承载力.故将钢管承载力乘增大系数1.1,对应的轴心受拉承载力计算公式为
Nut=1.1Asfy+Asrfyr+φ1Asbfyb (3)
式中:Asr、Asb分别为内配纵肋和钢骨面积; fyr、fyb分别为内配纵肋和钢骨的屈服强度; φ1为内配加劲件承载力修正系数,为内配加劲件应力与外钢管应力之比,该值由试验确定.
美国规范AISC360-16[27]和欧洲规范Eurocode4[28]对钢管混凝土受拉构件的承载力计算公式一致.不考虑内部混凝土对构件受拉承载力的提高,构件受拉极限承载力为加劲件和钢管的受拉承载力之和,相应计算公式为
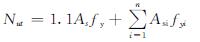(4)
Han等[10]不仅考虑内部混凝土对构件受拉承载力的提高,同时也考虑含钢率对钢管混凝土受拉构件承载力的影响,提出了普通钢管混凝土轴拉构件的承载力计算公式为
Nut=(1.0-0.4α)Asfy (5)
式中:α为构件的截面含钢率.
参考式(4),同时考虑内配钢骨和加劲肋对构件承载力的提高,同时内配钢骨和加劲肋的圆钢管混凝土构件轴心受拉承载力计算公式为
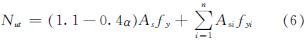
式中:Asi为加劲件面积; fyi为加劲件屈服强度.
研究表明,当试件跨中纵向应变达到5 000×10-6时,钢管已经处于屈服状态,且荷载-应变曲线的弹塑性阶段已基本结束,此后,随着纵向应变增长,荷载增长非常缓慢.因此,取跨中应变超过5 000×10-6[10]时对应的承载力作为试件的极限承载力并与上述各公式计算结果对比,如表6所示.由表可知,各公式得到的轴拉承载力计算值均小于试验值,结果偏于安全.对于普通圆钢管混凝土轴拉构件,《特殊钢管混凝土构件设计规程》(CECS 408:2015)、美国规范AISC360-16和欧洲规范Eurocode4、韩林海建议公式计算结果最大偏差分别为7.78%、16.05%、9.76%; 对于内配钢骨和纵肋的圆钢管混凝土轴拉构件,最大偏差分别为14.10%、18.89%、13.73%.
表6 构件轴拉承载力计算结果与试验结果对比
Tab.6 Comparisons of calculation results of bearing capacity and test results of axially tensioned members
《钢管混凝土结构技术规范》(GB50936-2014)[29]、《特殊钢管混凝土构件设计规程》(CECS 408:2015)[26]、AISC360-16[27]和Eurocode4-2004[28]规范均未给出钢管混凝土构件的轴拉刚度计算公式.Han等[10]基于试验和有限元分析结果,提出的圆钢管混凝土构件轴拉刚度计算公式为
(EA)t=EsAs+0.1EcAc (7)
式中:(EA)t为试件的整体刚度; Es、Ec分别为钢管和混凝土的弹性模量; As、Ac分别为钢管和内部混凝土的横截面面积.
对于内配纵肋构件,由于纵肋与外钢管焊接,可将纵肋与外钢管视为一体,计算构件整体受拉刚度时直接叠加纵肋的受拉刚度; 对于内配钢骨,在弹性阶段,内配钢骨与混凝土之间几乎未发生滑移,内配钢骨对构件的轴拉刚度贡献发生在混凝土开裂后.因此,参考式(7),提出内配加劲肋和钢骨的圆钢管混凝土构件轴拉刚度计算公式为
(EA)t=EsAs+EsrAsr+0.1(EcAc+EsbAsb) (8)
式中:Esr、Esb分别为内配纵肋和内配钢骨的弹性模量; Asr、Asb分别为内配纵肋和内配钢骨的横截面面积,其余变量物理意义与式(7)相同.
根据式(8)计算的试件轴拉刚度如表7所示.其中,(EA)tc为计算结果,(EA)t为试验结果,其值为试件荷载-应变曲线原点与钢材屈服点之间的斜率[10].(EA)tc/(EA)t的平均值为1.02,最大偏差为4%,计算结果与试验结果吻合较好.
表7 轴拉刚度计算值与试验值比较
Tab.7 Comparison of the calculated values of the axial tension stiffness with the experimental values
对7个不同内部构造的圆钢管混凝土试件进行了轴拉试验,结合有限元数值模拟和理论分析,得出以下结论:
(1)内配钢骨、纵向加劲肋试件的轴拉承载力较普通钢管混凝土试件分别提高13.60%和7.82%; 同时内配钢骨和纵向加劲肋试件的轴拉承载力较普通钢管混凝土试件提高22.94%.内配环肋对试件的轴拉承载力影响很小,但环肋能更有效地将外荷载传递给内部混凝土,使混凝土均匀受力;
(2)轴拉荷载下,混凝土率先开裂且几乎不承担外荷载,主要起支撑钢管、抑制钢管颈缩变形的作用;
(3)现有规范对于圆钢管混凝土构件轴拉承载力的计算偏于安全; 采用韩林海的建议公式所得的构件刚度与试验结果吻合较好.
