基金项目:中美政府间国际合作项目(2019YFE0100300); 黑龙江省自然科学基金优秀青年项目(YQ2019E024)
第一作者:黄 帅(1997-),男,硕士生,主要从事中深层地源热泵研究.E-mail:sds_hs@163.com 通信作者:董建锴(1982-),男,教授,博士生导师,主要从事热泵空调技术方面的研究工作.E-mail:djkheb@163.com
(1.哈尔滨工业大学 建筑学院,黑龙江 哈尔滨 150090; 2.寒地城乡人居环境科学与技术工业和信息化部重点实验室(哈尔滨工业大学),黑龙江 哈尔滨 150090; 3.北京市建设工程造价管理处,北京 101117; 4.中国建筑科学研究院有限公司,北京 100101)
(1.School of Architecture, Harbin Institute of Technology, Harbin 150090, China; 2.Key Laboratory of Cold Region Urban and Rural Human Settlement Environment Science and Technology (Harbin Institute of Technology), Ministry of Industry and Information Technology, Harbin 150090, China; 3.Beijing Engineering Cost Administration,Beijing 101117,China; 4.China Academy of Building Research, Beijing 100101, China)
medium deep geothermal energy; borehole heat exchanger; numerical simulation; heat recovery; engineering measurement
DOI: 10.15986/j.1006-7930.2021.06.008
建筑领域是造成直接和间接碳排放的主要责任领域之一[2],为降低建筑能耗,可再生能源在建筑供暖及供冷中得到了广泛的应用.在可再生能源中,中深层地热能资源丰富,具有清洁环保、储量大、稳定可靠等特点[3],近年来引起了行业人员的广泛关注.
与目前应用广泛的浅层地源热泵系统相比,中深层地源热泵系统具有换热器占地面积小、对全年冷热负荷平衡要求低等特点[4],并且,前者需同时满足冬季供热夏季制冷的需求,而后者仅用于冬季供热.因此,不同于浅层地源热泵系统需维持土壤全年热平衡,中深层地源热泵系统更侧重取热后对土壤的热衰减[5].前人对浅层地源热泵系统土壤热平衡做了相关研究[6-9],而中深层地埋管换热技术发展现状是工程实践先于理论研究[10],相关研究主要集中在完善数学模型[11-13]、中深层地埋管换热器取热特性[10, 14-16]等,而对岩土热恢复特性研究较少,贾林瑞等[17]对单取热工况地下岩土体温度热响应做了相关研究,发现1 400~1 800 m处的岩土温度变化率最快; 杜甜甜等[18]研究了中深层地埋管换热器取热对岩土的热影响,得出当延米换热量为100 W/m,运行20 a的最佳钻孔间距为133 m; 蔡皖龙等[19]研究了4种不同间歇运行模式下中深层地埋管换热器取热稳定性,发现当按不同运停比运行时的岩土温度恢复效果较好.
通过上述可知,中深层地热地埋管供热系统作为地源热泵系统的新形式,相关研究主要集于中深层地埋管换热器的取热特性,而对钻孔外岩土的热恢复特性等研究较少,并且,中深层地埋管换热器的埋管深度往往达数千米,地下岩土环境具有不确定性,应用实验方法研究岩土热恢复较为困难.为此,本文建立数值传热模型,基于有限差分法将控制方程离散求解,将求解的结果与实测数据进行比对,分析了中深层地埋管换热器周围岩土温度场变化,旨在揭示岩土温度在热恢复阶段的变化规律,为工程实践提供理论指导和依据.
中深层同轴套管式地埋管换热器的取热原理如图1所示,在循环水泵的驱动下,循环水由套管外部环腔流入,经中深层的高温岩土加热后通过内套管反向流动,流出地面后进入热泵机组.
中深层地埋管换热器的取热过程主要包括内套管流体与外部环腔流体的对流换热、环腔流体与外管壁的对流换热以及外套管与周围岩土的导热,其换热过程较为复杂,并且地下岩土环境具有不确定性,因此做出以下假设:
(1)忽略地下渗流作用的影响,将岩土中传热视为单纯的导热问题[20];
(2)忽略地表温度波动的影响[21];
(3)假定数值模拟区域的径向边界处的温度分布不受地埋管换热器的影响;
(4)假定同轴套管式换热器内循环体主要以对流传热,忽略其轴向的热传导.
基于以上假设,每层岩土的导热方程可写为[22]

式中:ak为不同岩土层的热扩散率,m2/s; Ts为岩土层温度,℃; Δτ为时间步长,s; r和z为径向长度与竖直方向长度,m.
当地埋管换热器内的循环水按照图1所示的方式流动时,外部环腔内流体的能量方程为
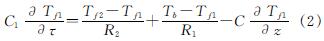
内管流体的能量方程为

式(2)和(3)描述的是在地埋管换热器正常取热工况下的能量方程,当系统停运时,外部环腔内流体及内管流体的流速为零,此时地埋管周围岩土层处于热恢复状态.与正常取热工况下的能量方程相比,此时对流项前的系数C为零.
其中:
C1=(π)/4(d21i-d220)ρc+(π)/4(d210-d21i)ρ2c2+(π)/4(d2b-d210)ρgcg(4)
C2=(π)/4d22iρc+(π)/4(d220-d22i)ρ1c1(5)
式中:C=MCf指的是循环液的热容流量,kJ/(s·K); db代表钻孔半径,m; di和do代表套管的内径和外径,m; ρc、ρ1c1、ρ2c2、ρgcg分别代表循环水定容比热、外管定容比热、内管定容比热、回填材料定容比热,J/(m3·K).此外,外管内循环水和钻孔壁之间的热阻R1以及内外管循环水之间的热阻R2分别由下式求得:
R1=1/(πd1ih1)+1/(2πkp1)ln((d10)/(d1i))+1/(2πkg)ln((db)/(d10))(6)
R2=1/(πd2ih2)+1/(2πkp2)ln((d20)/(d2i))+1/(πd2h1)(7)
式中:kg,kp1和kp2代表回填材料、外管和内管的导热系数,W/(m·K); h1和h2代表套管外管和内管的对流换热系数,W/(m2·K).
岩土中的初始温度分布在径向是均匀的,而在纵向存在地温梯度,并且不同岩土层的地温梯度不同,因此,在大地热流一定的条件下,在任一埋管深度处的初始岩土温度可以表达为下式[23].
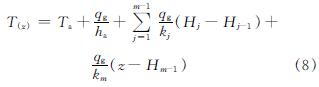
在圆柱坐标的径向边界rbnd(距离地埋管换热器的中心足够远)设第一类边界条件,认为该处的温度分布不受地埋管换热器取热的影响,同时,在距离钻孔底部较远位置处(钻孔底部以下200 m处)也设第一类边界条件.
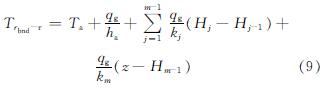
式中:Hj是第j层地层底部的坐标; qg是大地热流,W·m2; Ta是地表温度,℃; ha是空气与地表的对流换热系数,W·(m2·K); km为岩土的导热系数,W·(m·K).
在地表的边界设定第三类边界条件,同时,考虑到钻孔深度往往达数千米,地表的参数的变化对地埋管换热器取热影响较小,因此在本模型中求解过程中假定地表以上的空气温度Ta以及表面对流换热系数ha保持不变[24].
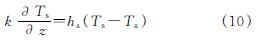
外部环腔流体与内管流体能量方程的边界体条件为
Tf1=Tf2-Q/C,Z=0(11)
Tf1=Tf2,Z=H(12)
式中:Q为取热功率,kW; C=MCf指的是循环液的热容流量,kJ/(s·K); Z是埋管深度,m.
在非稳态数值传热模拟中,时间步长Δτ、纵向步长Δz及径向步长对模拟计算速度及结果的精确度均有一定影响.为了保证结果的准确性需要对其做无关性验证,由图2时间步长无关性验证结果可知Δτ可取900 s.考虑径向较远处热流趋近于零,钻孔附近的热流及温度梯度较大,故以钻孔壁为界采用变步长,即径向步长按照等比级数变化(等比系数取1.2),距离钻孔第一个节点的距离为0.168 m,径向共取40个节点,并且纵向步长Δz取10 m.由图3可知节点数量可取7 700个,满足计算精度要求.此外,岩土热物性参数见表1[14, 25],模拟所需的基础物理参数见表2.
为验证建立的数学模型及所编程序的准确性,我们对西安市某住宅工程进行了现场实测[14, 26].在2019年到2020年供热期间,共监测了某地热井1 100 h的进出口温度,测试期间单孔地热井平均换热量为270 kW,循环水平均流量为25.5 m3/h,地埋管换热器进出水温差约为9.2 ℃,机组的平均COP达4.7.将该地热井运行参数导入所编制的程序,进而得出模拟地源侧进出口温度值,其中,地源侧进出水温度的模拟值与实测值比对如图4所示.
图4 地源侧进出口温度实际值与模拟值比对[14]
Fig.4 Comparison of actual and simulated temperature at the inlet and outlet of the ground source side
从图4可以看出,650 h后实测地埋管换热器出水温度与模拟出水温度的最大相对误差为6.01%,满足工程要求,进而为下文相关分析奠定了基础.
本文把寒冷地区住宅建筑作为模拟对象,其供暖周期一般为当年11月15至次年3月15日,约120 d,中深层地埋管换热器在供暖期运行,其他时间停机,停机期间其周围岩土处于热恢复期.图5分别给出了中深层地埋管换热器连续取热120 d后以及经过为期8个月热恢复后的岩土温度场,此时的流量为28 m3/h时,其他参数如表2所示.
图5 中深层地埋管换热器周围岩土温度分布
Fig.5 Temperature distribution of rock and soil around medium deep borehole heat exchanger
从图5(a)可以看出,中深层地埋管换热器连续取热后,其周围1 000 m以下的岩土温降较为明显,但在埋管深度200 m以上的岩土温度有所升高.分析原因:地埋管换热器主要从温度较高的中深层岩土取热,而浅层岩土温度较低,内管流体经中深层岩土加热后,流体温度将高于浅层岩土,管内流体会向浅层岩土逆向传热.因此,为降低热损失在浅层岩土区域应采取相应的保温措施.此外,从图5(b)可以看出,岩土经过8个月的热恢复期,与初始岩土温度场相比,径向距离10 m以内的岩土恢复程度较高,下文将对岩土热恢复程度做详细分析.
为进一步分析中深层地埋管换热器连续取热对其周围岩土温度场的热影响,图6给出了中深层地埋管换热器运行120 d后不同埋管深度径向岩土温度分布.
图6 中深层地埋管换热器运行120 d后不同埋管深度径向岩土温度分布
Fig.6 Radial geotechnical temperature distribution at different depths after 120 days operation of medium deep borehole heat exchanger
从图6可以看出,在中深层地埋管换热器连续运行120 d后,与不受影响的径向岩土温度相比,当r=0.2 m,z分别为1 000 m、1 400 m、1 800 m和2 000 m时,温降分别为17.1 ℃、20.5 ℃、21.2 ℃和22.1 ℃,此外,z=1 000 m和z=2 000 m时的岩土热影响半径分别为6.4 m和9.3 m.因此,为研究中深层地埋管换热器周围岩土的热恢复性问题,将模拟监测点主要设置在岩土受热影响的区域,即r<9.3 m范围.
图7 模拟监测点位置[27]
Fig.7 Location of monitoring points
模拟监测点的位置如图7所示,径向r分别取0.3 m、0.4 m、0.5 m、1 m、1.5 m、2 m、4 m和6 m,径向z分别取400 m、800 m、1 200 m、1 600 m、1 800 m和2 000 m,共设置48个模拟监测点.
从图8可以看出,运行初期中深层地埋管换热器周围岩土(z=400 m)的温度有所升高,主要原因是运行初期套管内流体温度较高,热量由套管内的流体传向周围岩土,经过一段时间运行后,套管内的流体温度逐渐降低,热量逐渐由周围岩土传向管内流体.下文图中出现的类似现象在这里进行说明,后期不再赘述.
图8 z=400 m处不同径向距离岩土温度
Fig.8 Temperature distribution of monitoring points with different radial distances at z=400 m
图9给出r≤1 m范围内24个监测点全年温度分布,此部分区域岩土距离地埋管换热器较近,属于中深层地埋管换热器取热的核心区域.
从图9可以看出,在埋管深度相同的取热阶段,越靠近中深层地埋管换热器的岩土温降越大.当z=2 000 m,r分别取0.3 m、0.4 m、0.5 m及1 m时,温降分别为18.6 ℃、16.2 ℃、15.1 ℃、10.5 ℃.主要是在取热阶段,以中深层地埋管换热器为中心向周边岩土层取热,因此温降随着径向距离的增加而降低.此外,当r=0.3 m,z分别取400 m、800 m、1 200 m、1 600 m、1 800 m及2 000 m时,温降分别为4.1 ℃、10.7 ℃、15.3 ℃、17.1 ℃、17.8 ℃和18.6 ℃.由此可知,中深层地埋管换热器的取热区域主要集中在1 200~2 000 m的岩土,此外,在岩土热恢复阶段,可以看出前期斜率较高后期趋于平稳,即前期岩土的热恢复速率较快,下文将进行相关分析.
图 10给出1 m<r≤6 m范围内24个监测点全年温度分布,与r≤1 m范围内24个监测点相比,此部分区域距离中深层地埋管换热器较远,但其变化规律与前文分析相同.
从图 10可知,当半径r从1.5 m变化到6 m时,不同埋管深度的岩土温度变化幅度均逐步下降.当半径r增大到2 m时,z=400 m处岩土温度变化幅度较小; 当半径r增大到4 m时,z=800 m及以上的区域岩土温度变化幅度较小; 当半径r增大到6 m时,不同深度处的岩土温度变化幅度均较小.当埋管深度相同,以z=2 000 m为例分析,r分别为1.5 m、2 m、4 m和6 m时,在中深层地埋管换热器取热阶段时所对应的温降分别为8.2 ℃、6.0 ℃、3.1 ℃和0.9 ℃,表明中深层地埋管换热器对其周围岩土的热影响范围有限.
为进一步分析岩土热恢复阶段的温度分布规律,图 11给出了32个监测点随时间的温度分布.
由图 11可以看出,前期岩土层热恢复速度较快,后期热恢复速度较为平缓.以z=2 000 m位置不同径向距离的岩土为例,z=2 000 m处不同径向距离的岩土初始温度为63.0 ℃,经过120 d的连续取热后r为0.3 m、0.4 m、0.5 m和1 m处的岩土温度分别是44.5 ℃、46.8 ℃、48.0 ℃和52.6 ℃,经过为期2个月的热恢复后的温度约为59.7 ℃,而经过为期4个月、6个月、8个月热恢复后的温度约为60.9 ℃、61.6 ℃和61.9 ℃.分析原因:钻孔壁附近岩土经过为期4个月的连续取热后温度下降到最低,此时,与周围相同深度未受影响的岩土相比温差达到最大,在大温差的作用下,从周围未受影响的岩土向地埋管中心传递的热传导作用强,但后期随着岩土温度逐渐恢复,与临近岩土的温差进一步降低,热传导作用不明显,因此,当岩土温度恢复到一定数值后再进行恢复,热恢复速率会明显降低.但经过为期8个月的热恢复过程后,不同径向距离处的温度基本能够恢复到初始状态.
图 12给出r=0.3 m埋管深度分别为1 200 m、1 600 m、1 800 m和2 000 m的岩土在不同时间段的热恢复率,从图 11中可以看出,在相同热恢复时间段内,埋管深度在1 200 m的岩土热恢复率最高,主要原因是中深层地埋管换热器对其热影响较小,并且不同时间段岩土的热恢复率均在97.9%以上.而当z=1 600 m时,恢复两个月及八个月的热恢复率分别为94.4%和97.9%; 当z=1 800 m时,恢复两个月及八个月的热恢复率分别为94.0%和98.0%; 当z=2 000 m时,恢复两个月及八个月的热恢复率分别为94.7%和98.2%.
图 12 r=0.3 m处不同埋管深度的岩土热恢复率
Fig.12 Thermal recovery rate of rock and soil with different depths at r=0.3 m
此外,从图 11中也可以看出,热恢复率随着恢复时间的增加而逐渐减小,以z=2 000 m为例进行分析,以恢复两个月的热恢复率为基准,热恢复4个月、6个月、8个月热恢复率在前一基础上分别增加2.1%、0.9%和0.5%.通过上述分析可知,经过为期8个月的热恢复期,岩土能够基本恢复至初始温度.
为揭示中深层地埋管换热器周围岩土的热恢复特性,本文建立了数值传热模型,基于有限差分法进行求解,并将求解的结果与实测数据进行比对,在此基础上分析了中深层地埋管换热器周围岩土全年的温度场变化.主要得出以下结论:
(1)中深层地埋管换热器对其周围岩土的热影响范围有限.当埋管深度为2 000 m时,r分别为1.5 m、2 m、4 m和6 m时,在中深层地埋管换热器取热阶段时所对应的温降分别为8.2 ℃、6.0 ℃、3.1 ℃和0.9 ℃,其岩土热影响半径为9.3 m;
(2)中深层地埋管换热器的取热区域主要集中在1 200~2 000 m的岩土.当r=0.3 m,z分别取400 m、800 m、1 200 m、1 600 m、1 800 m及2 000 m时,所对应的岩土温降分别为4.1 ℃、10.7 ℃、15.3 ℃、17.1 ℃、17.8 ℃和18.6 ℃;
(3)岩土热恢复率随着恢复时间的增加而逐渐减小,前期热恢复的速率较快,后期趋于平稳.当z=2 000 m时,以恢复两个月的热恢复率为基准,热恢复4个月、6个月、8个月热恢复率在前一基础上分别增加2.1%、0.9%和0.5%;
(4)经过8个月的热恢复期,岩土能够基本恢复至初始温度.当r=0.3 m,埋管深度为1 200 m、1 600 m、1 800 m和2 000 m的岩土所对应的热恢复率分别达98.7%、97.9%、97.9%和98.2%.