混凝土的本构模型是进行有限元分析的基础.目前,常用韩林海^[11]提出的约束混凝土本构模型,钢管与核心混凝土之间的相互作用通过套箍系数ξ来表达,表达式为

ξ=A_sf_y/A_cf_c (1)

式中:A_s为钢管横截面面积,mm²; A_c为混凝土的横截面面积,mm²; f_y为钢材屈服强度,MPa; f_c为混凝土轴心抗压强度设计值,MPa.

UHPC剔除了粗骨料,在材料组成上与普通混凝土有较大不同,这使得UHPC的材料性能与普通混凝土相比有较大差异,所以约束普通混凝土本构模型并不能完全适用于钢管UHPC构件的数值分析.课题组通过钢管UHPC短柱轴压试验,对钢管约束UHPC轴压本构模型进行了研究^[12],结合UHPC的材料性能试验结果,对约束UHPC的峰值应变ε₀、抗压强度f_c和弹性模量E₀特征参数进行了推导,其表达式为

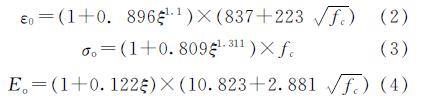
在韩林海本构模型的基础上进行了一定的修正,建立了钢管约束UHPC轴压本构模型,适用性较好,其表达式为

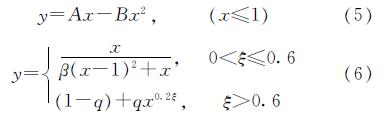
式中:x=ε/ε₀,y=σ/σ₀; A=2-k,B=1-k,k=0.434ξ; β=0.015ξ^2.176; q=0.434ξ/(22.957ξ-9.081).

钢材本构通常采用二次塑流模型,将应力—应变曲线简化为五段直线,如图1所示.应力—应变关系式见式(7).

图1 钢材本构模型
Fig.1 Constitutive model of steel

式中:f_y为钢材抗拉强度设计值; ε_p=0.8f_y/E_s; ε_y1=1.5ε_p; ε_y2=10ε_p; ε_u=100ε_p; A=0.2f_y(ε_y1-ε_p)2; B=2Aε_y1; C=0.8f_y+Aε²_p-Bε_p.分析中设钢材为各向同性材料,采用Mises屈服准则,各向同性强化.

通过使用位移控制,将单向轴荷载施加到柱端部.为了便于计算,耦合点位于柱底部中心处,并限制参考点的所有自由度.如图2所示.钢管采用壳(Shell)单元,UHPC和上下端板均采用三维六面体八节点(C3D8R)实体单元.为减少有限元模拟时间,在保证计算精度的同时调整计算样本,计算出适合本文模型的种子分布和网格划分网格单元大小划分为10 mm.

图2 边界条件和网格划分
Fig.2 Boundary conditions and element meshing

钢管与UHPC的接触面设置为完全接触,法向方向采用硬接触(Hard Contact),钢管做主表面,UHPC做从表面.在切向行为中,库伦摩擦(Coulomb Friction)模型能有效模拟钢管与UHPC之间的相对滑动摩擦力,摩擦公式选用“弹性滑动”的罚函数(Penalty),本文通过对钢管UHPC短柱进行了多次试算发现,将摩擦系数值μ取为0.6可以取得与实验值整体符合较好的计算结果,因而本文计算中取μ=0.6.

对文献[10]和[13]中共28个方钢管UHPC轴压短柱试验试件进行有限元模拟,选取其中8个ξ不同的试件,有限元计算得到的荷载—位移曲线与试验结果比较如图3所示.由图可知:两者吻合较好,跨中截面位移和峰值荷载基本一致.但是,有限元模拟没有考虑到试件在制作过程中,钢管中UHPC的分布不均匀,以及试件在试验过程中钢管焊缝开裂的影响,导致有限元计算结果与试验结果有一定差异,部分试件的模拟曲线的整体弹性模量稍大于试验曲线,且下降段的承载力有略微提升现象.

图3 荷载—位移曲线
Fig.3 Load-displacement curves

将28个试件的极限承载力试验值与本文有限元模拟的计算值列于表1.由表1可知,有限元计算值与试件试验值之比的平均误差4.96%,总体上有限元计算结果与试验结果吻合较好.

表1 试件参数及峰值荷载对比
Tab.1 Comparison of specimen parameters and peak loads

试验试件的破坏形态主要包括剪切型破坏和腰鼓型破坏两种^[9],针对这两种类型的破坏分别取典型试样,并将数值分析得出的破坏模式与试验结果进行比较,发现试件破坏形式的主要影响因素是套箍系数ξ.图4和图5显示了两种破坏的整体变形、钢管峰值应力云图和最终破坏时x轴截面的塑性拉伸应变云图.由图可知,当套箍系数较小时,发生剪切型破坏.随着荷载的增加,UHPC内部产生斜裂缝并不断延伸至其形成上下错动两部分; 达到极限荷载时,钢管内核心UHPC部分被压坏,局部钢管产生一定的突起,并且向附近截面扩展.当套箍系数较大时,发生腰鼓型破坏.随着荷载的增加,试件中部区域发生严重压缩变形; 加载结束时,试件中部四面突起且相互贯通,形成一道或者多道褶皱环,且方钢管的角部出现应力集中现象,发现钢管对核心UHPC的角部约束强,中间约束差.

综上可见,利用有限元模拟的结果与试验试件的破坏形态吻合较好.本文使用的建模方法、材料本构、边界条件、网格划分和接触条件等设置能够有效的模拟方钢管UHPC短柱轴心受压力学性能,可用于实际工程中的结构分析与计算.

图4 剪切型破坏
Fig.4 Shear type damage

图5 腰鼓型破坏
Fig.5 Girdle type damage

通过对方钢管UHPC短柱的轴压试验数据和的大量有限元模拟结果进行统计分析,得到典型的轴向荷载—位移曲线,如图6所示.方钢管UHPC轴心受压短柱试件的受力过程可概括为三个阶段:弹性工作阶段、弹塑性工作阶段和塑性流动阶段.

(1)弹性工作阶段(oa段):本阶段的荷载—位移曲线基本呈直线状态,钢管的外形变化不明显,UHPC也没有开裂,试件的初始刚度基本保持不变.钢管对核心UHPC还没有起套箍作用,钢管和核心UHPC近似于单独受力.

(2)弹塑性工作阶段(ab、ac、ad段):随着轴压荷载的不断增大,核心UHPC内部的微裂缝开始扩展延伸,此时钢管对其的套箍作用开始发挥,钢管对核心UHPC的四个角部出现不同程度的应力集中现象,核心UHPC可以划分出有效约束区和弱约束区.

(3)塑性流动阶段阶段(be、cf、dg段):对文献[10]和[13]共28个试验数据和大量有限元模拟结果进行统计分析,发现在不同套箍系数ξ下,钢管对核心UHPC的约束作用不同,可分为三种类型.当套箍系数ξ≤2.50时,曲线先出现明显的下降段,而之后进入平稳工作阶段; 当套箍系数2.50≤ξ≤3.48时,试件表面变形继续膨胀,但轴压荷载基本维持不变; 当套箍系数ξ≥3.48时,轴压荷载随试件表面变形增长而缓缓增加.

图6 试件的典型荷载—位移曲线
Fig.6 Typical load-strain curves of specimens

本文以文献[10]中的A1T5试件作为基本研究对象,进一步研究试件在不同宽厚比、钢管强度和UHPC强度下,其对有限元模拟得到的荷载—位移曲线的影响规律,如图7所示.可以观察到:

(1)当其他因素保持不变时,试件的承载力随着宽厚比的增大呈非线性下降.随着截面宽厚比的降低,试件的荷载—位移曲线下降段的斜率降低,初始刚度增大,残余承载力也随之提高;

(2)当其他因素保持不变时,试件的承载力随钢管屈服强度的增大呈线性增长,延性得到改善.钢管强度的变化对初始刚度的影响较小,对试件整体的荷载位移曲线影响规律较为一致;

(3)当其他因素保持不变时,试件承载力的增长基本上与UHPC强度的增长呈线性关系.试件在弹性变形阶段,试件的初始刚度受UHPC强度的影响不大; 试件承载力与UHPC强度的提高呈线性增长,但是在荷载—位移曲线的下降段斜率逐渐增加,说明延性在逐渐变差.

图7 不同因素对荷载-位移曲线的影响
Fig.7 Effect of different factors on the load-displacement curves

采用极限平衡法推导方钢管UHPC短柱的轴压承载力,本文计算基于以下假设:

(1)柱竖向荷载由钢管和核心UHPC承担,方钢管UHPC柱可视为由钢管和核心UHPC组成;

(2)当试件破坏时,钢管屈服,核心UHPC达到极限抗压强度.

Varma等^[14]提出将方钢管对核心混凝土的约束可以分为有效约束区和弱约束区,如图8所示.图8中,L为方钢管边长; t为钢管厚度; θ为约束界限边切角.假定有效约束区与弱约束区的边界视为二次抛物线,取θ=45°.

图8 核心混凝土的有效约束区
Fig.8 Effective constraints of core concrete

核心混凝土有效约束系数k_eq表达式如下.

k_eq=k₁·k_e (8)

式中:k₁为横截面侧面有效约束系数,取k₁=1; k_e为横截面有效约束系数,k_e=A_e/A_c, A_e为有效约束区混凝土截面面积,A_c为核心混凝土截面面积.

弱约束区混凝土面积A_e1=2(L-2t)²/3,有效约束区混凝土面积A_e=A_c-A_e1=(L-2t)²/3,代入式(8)可得k_e=k_eq=1/3.

设核心混凝土对方钢管内表面提供的侧向压力为σ_r,环向应力为σ_θ.由作用力及反作用力原理可知,核心UHPC所受到钢管的侧向约束应力与核心UHPC对钢管的侧向应力是一对相互作用力,对钢管进行受力分析,受力简图如图9所示.

图9 方钢管受力简图
Fig.9 Forced diagram of square steel pipe

由平衡条件可得

σ_r=(2σ_θt)/(L-2t) (9)

钢管对核心混凝土的等效侧向压应力为

σ'_r=k_eq·σ_r (10)

本文采用Mander^[15]提出的约束混凝土本构能够很好地反映方钢管对核心UHPC的约束机理,表达式为

式中:f_cc为约束混凝土轴压强度; f_c为混凝土轴心抗压强度.

依据静力平衡条件可得

N=A_cf_cc+A_sσ_z (12)

加载过程中σ_r为σ_z的2%左右,计算时可忽略不计,钢管屈服采用Von Mises屈服条件,即

σ²_z+σ_zσ_θ+σ²_θ=f²_y (13)

联立式(8),(9)得

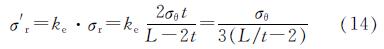
考虑到钢管相对混凝土截面较薄,有

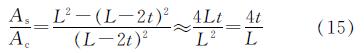
由式(13)～式(15)得

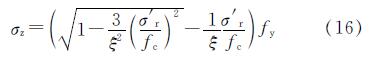
由式(10),(11),(12),(16)得

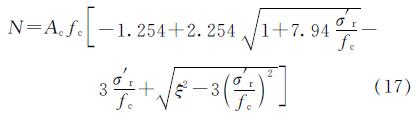
根据极值条件dN/dσ'_r=0,有

N_u=A_cf_c(1+αξ) (18)

将式(18)变换后得N_u/A_cf_c=1+αξ,以套箍系数ξ作为横坐标N_u/A_cf_c作为纵坐标,将文献[10]和[13]的试验数据进行拟合,如图 10所示.可得方钢管UHPC短柱的轴压极限承载力为

N_u=A_cf_c(1+1.12ξ) (19)

图 10 试验数据与拟合曲线
Fig.10 Test data and fitting curves

采用本文公式(20)对文献[16-17]共33根方钢管UHPC短柱试验试件进行承载力计算,将试验值N_e、计算值N_s和N_e/N_s二者的比值列于表2中.由表可知,本文提出的轴压承载力公式的计算值与试验实测值之比的平均值为1.019,标准差为0.073,两者吻合较好.

图 11给出了本文公式计算的结果与试验结果关系图,由图可知本文推导公式在套箍系数ξ为1.25～6.07,UHPC轴心抗压强度在92.5～141.0 MPa范围内,具有较好的适用性.

表2 公式计算与试验结果的对比
Tab.2 Comparison between formula calculation and test results

图 11 公式计算与试验结果对比
Fig.11 Comparison between formula the calculation and test results