基金项目:陕西省社发重点基金项目(2017ZDL-SF-16-5,2017ZDCXL-SF-03-02)
第一作者:王 茜(1996—),女,硕士生,主要研究方向:智能建筑. E-mail:781871461@qq.com.通信作者:于军琪(1969—),男,教授,博导,主要研究方向:智能建筑.E-mail:junqiyu@126.com
(School of Building Services Science and Engineering, Xi'an Univ. of Arch. & Tech., Xi'an 710055,China)
energy consumption forecast; university library; similar day; Levenberg-Marquardt algorithm
DOI: 10.15986/j.1006-7930.2022.03.017
我国有近2 000余所高校, 其能耗在社会总能耗中的占比达到8%[1].在高校内,不同建筑类型的能耗因建筑而异[2].图书馆在高校建筑中必不可少,是学生和教职人员的聚集地,人流量大,这导致了其能耗较高的特点,高彪等[3]以长三角地区某高校为例,发现图书馆建筑在高校建筑中以仅5%的占地消耗了12%的能量.同时,图书馆的节能潜力也很大,有研究表明高校图书馆建筑有6%~29%的节能潜力[4].如何既能保证使用者需求得到满足,又可以减少图书馆的不必要能耗成为一个研究问题.Filho等[5]通过持续跟踪大学能耗数据,研究了解居住者对高校能耗的影响.Wang和Shao对大学图书馆进行了持续一个月的数据收集工作,他们最终发现图书馆具有独特的能耗模式[6].因此,建立高校图书馆能耗预测模型对节能降耗有重要意义.
过去常使用工程学和统计学方法对能耗进行预测[7].在使用工程学方法的基础上,Yik等[8]提出了更加简单准确的建筑的冷负荷模型.2018年来自伊朗的Mohammad Sepehr及其同事在对当地一百多所建筑的能耗数据进行研究时,就通过统计学方法建立了相关预测模型[9].工程学方法建立预测模型通常被认为是较为准确和有效的,但实践中由于需要大量详细信息和参数的支撑,通常实现较为困难.统计学方法出现较早,理论和技术通常被认为更加成熟,但其普适性不够强,并且准确程度也很难达到较高的水平.近些年来,通过人工神经网络(Artificial Neural Network,ANN)建立预测模型的方法逐步完善,相比于传统方法的种种弊端,其模型的普适性较强,可与不同方法组合使用,且预测结果通常具有较高的准确性.国内外一些研究已经证实,神经网络预测模型在很多场景下有较为突出的表现[10-12].
图书馆建筑具有人员数目变化大,影响其能耗影响成因复杂,且不同因素的影响不同等特点.为了对高校图书馆建筑能耗进行相对简单且准确的预测,本文提出一种基于模糊聚类的相似日筛选和列文伯格-马夸尔特(Levenberg-Marquardt, LM)神经网络算法结合的能耗预测模型.同时,为了对模型的预测结果进行评价,引入三种评价指标.将本文所提模型与传统LM能耗预测模型进行比较,验证本文所提方法在预测结果准确性方面的优越性.
通常把多种特征,如日期、温度和湿度等,都近似的几日称之为相似日.由于状态的相似性,这些日期中产生的能耗通常更为趋同.利用这一特性,在能耗预测中使用相似日法可提高预测结果的准确性.
通常使用特征向量来对相似日进行描述.能耗预测中的特征向量一般由对能耗影响较为重要的因素构成.为选取此类因素,使用了数据分析法对能耗数据进行了研究.特征向量确定以后,再制定选取相似日的判断规则.在相似日选取结束后,将筛选出的数据导入预测模型,从而使模型的准确性提高[13].
以往使用相似日法时,由于相似日的界限通常较为模糊,选取过程往往依赖经验.但受制于人主观判断的影响,选取结果可能会存在较大的偏差.为了减少可能存在的结果偏差,同时又由于判断界限不分明的原因,使用模糊聚类的方式对相似日法中相似日的选取进行了改进.
根据某些标准将特定事物的集合进行分类的过程被称为聚类分析[13].早期的聚类分析通常对判定界限有着明确的规定,这种聚类方法简单、快捷,非常适用于构成较为单一且事物界限分明的场景中.然而一旦需要处理界限不明确的复杂问题,传统聚类方法并不适用.在传统方法无法解决的复杂问题中,通常使用模糊聚类的方法.这种方法利用模糊数学的原理,将客观事物的关系通过其特征加以确定,并据此对其进行分类[13-14].
模糊聚类需要建立模糊矩阵:
样本集X={x1,x2,…,xn },特征向量为xi=(xi1,xi2,…,xim).其中,n表示样本数,m为特征向量数.因此,样本集X的特征矩阵表示为

聚类过程中需要对相似度进行确定.相关的方法非常多,距离法就是最为常见的一种.距离法中包含的计算方式也多种多样,用于不同情境下的距离计算,如欧氏距离、夹角余弦等等都是较为常见的距离计算方法.其中欧氏距离计算简便,应用广泛,适用于本研究场景.此次使用此方法计算xi=(xi1,xi2,…,xim)和xj=(xj1,xj2,…,xjm)之间的相似度rij.
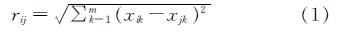
样本集X的模糊矩阵为

其中i,j=1,2,…,n.
中间距离法是一种使用中间距离对类间距进行定位的方法,是系统聚类过程中的常用方法之一.相比于另外两种常见的类间聚类方法(最长距离法和最短距离法),这种方法可以既有保有相同的优势,又去掉了二者的缺陷.因此,在此次模糊聚类过程中使用此方法对类间距进行计算.
梯度下降法和高斯—牛顿法都是神经网络中的常用算法,而列文伯格-马夸尔特算法或称阻尼最小算法[15],是一种将二者进行结合的方法.这种结合算法同时具备两种方法的优势——全局特性和高效收敛.并且由于在解决各类非线性问题上具有优势[16],其应用领域较广,涵盖经济、管理、设计等各个方面.
在传统前馈神经网络的基础上,使用LM算法代替梯度下降法寻求最优化问题的解,这种改进后的BP神经网络一般被称为LMBP神经网络或者简称LM神经网络[7].
与BP神经网络相似,LM神经网络的训练过程也需要进行正向传播过程和反向传播过程.在正向传播过程中,两种神经网络的训练过程基本相同.而在第二步过程中,各层学习参数由LM算法经调整后得到.最终,误差收敛并稳定在合适区间后,停止训练[17].LM算法对学习参数进行修正过程如下:
训练误差ε、系数u0以及权重与阈值向量X(0)均已确定.
目标函数为平方误差函数,其公式如下.
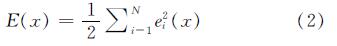
式中:ei(x)为第i个预测值和实际值的误差.
X(k)=X(k-1)+ΔX(k-1) (3)
式中,X(k)表示第k次循环的向量
ΔX的公式为
ΔX=-J(x)e(x)/[JT(x)J(x)+uI] (4)
式中,u表示比例系数,且u>0,I表示单位矩阵,J(x)表示雅可比矩阵
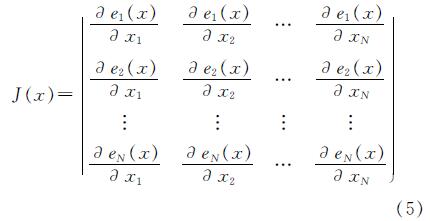
当E(X(k))<ε时完成预测.否则,将权重与阈值向量更新为X(k+1),计算误差函数E(X(k+1)).若E(X(k+1))<E(X(k)),则k=k+1,u=u/β,重新计算E(X(k+1)).反之,则X(k+1)=Xk,u=u/β,再次计算ΔX和E(X(k)).
实例建筑来源于西北某高校图书馆,其室内人员数据根据门禁系统记录计算得到,其能耗数据来自高校内部的能耗监管平台,所使用的当地日均气温数据来自中国气象数据网.
图书馆的暑期时间表由2020年7月13日起实行至当年8月13日止,如表1所示.
表1 暑假图书馆开放时间表
Tab.1 Library opening schedule during summer vacation
表1 暑假图书馆开放时间表
Tab.1 Library opening schedule during summer vacation
图书馆的学期开放时间表由2020年8月14日起开始实行,如表2所示.需要说明的是,在2020年10月1日至10月4日期间,由于节假日的缘故,除公共自习室于8:00—22:00开放外,其他区域关闭.
表2 学期图书馆开放时间表
Tab.2 Library opening schedule during terms
表2 学期图书馆开放时间表
Tab.2 Library opening schedule during terms
考虑可用性数据和研究价值,选取2020年7月14日至2020年11月30日的共6 700多条(包含能耗、气温和人数)数据进行研究.需要说明的是,能耗数据在2020年9月4日至7日出现记录缺失,但由于缺失的数据量很小,该缺失对整体研究结果造成的影响非常有限,因此,将其忽略.
本研究对象为图书馆能耗,为确定其相似日特征向量及预测模型的输入参数,需要筛选出对该建筑物能耗影响较为重要的因素.因此,使用数据分析法对室内人员人数、日均气温与能耗数据进行了研究.
如图1所示,能耗存在三个高峰,包括两个夏季高峰和一个冬季高峰.如图2所示,夏季高峰期间,日平均气温高,而冬季高峰期间,日均气温断崖式下跌.为维持室内温度适宜,空调系统耗能较大.由此可知,气温对图书馆建筑能耗产生的影响不可忽视.
能耗于7月12日后出现快速大幅下跌.此时图书馆由于暑假原因调整开放策略,只图书馆总服务台及自修室开放,其他服务区域等基本全部关闭.由此产生的大量照明系统及其他系统相关设备的关闭导致此时能耗下跌严重.而在8月14日进入学期开放状态后,图书馆建筑能耗逐渐回升.因此,图书馆开放策略的调整会影响图书馆能耗的变化.
拟合度((R-squared,R2)可用来表示关系的线性程度,通常情况下,该值越接近1,则表示线性关系越明显.表3利用R2对室内人员和能耗之间的关系进行了统计.从表3中可以发现,能耗的波动与室内人数的变化存在一定关系,但各月份R2存在较大波动,即室内人员对能耗的影响程度在不同时期存在差别.结合前文对气温和开放策略对图书馆能耗的影响分析可推测,在某些月时期,气温或开放策略对能耗的影响超过了室内人员的影响,而其他时期反之.根据实际数据,R2在7月下半月为0.678 5,在9月下半月为0.912,在11月上半月为0.441 2,均显著高于当月总体R2,且发生时间与气温或开放策略发生显著变化的时间大致吻合.由此可知,室内人数变化对该建筑能耗具有一定影响,但由于存在其他影响因素的相互作用,其影响程度会有所不同.
表3 图书馆室内人员与能耗的R2统计表
Tab.3 R-square value of the occupancy and the energy consumption in the library
表3 图书馆室内人员与能耗的R2统计表
Tab.3 R-square value of the occupancy and the energy consumption in the library
综上所述,室内人员人数、气温和图书馆开放策略都是对能耗影响较大的因素.
相似日LM神经网络预测模型的预测流程如图3所示.
LM神经网络的结构通常是一层输入层、一至多层隐含层和一层输出层.其中,输入层和输出层的节点数由输入和输出的数据类型数决定.
根据2.2节数据分析,图书馆服务区域的逐时开放状况可作为一个参数进行输入.但由于开放状况无法直接以数字形式输入,因此,在进行模型构造前需要对其进行量化处理.将图书馆各区域分别进行参数设定,如表4所示.图书馆某时刻开放数据可由当时图书馆开放区域的参数累计得到,因此具体量化数据需参照表1与表2后获得.
气温也会影响图书馆能耗,但由于逐时气温数据较难取得,所以使用日平均气温作为一个输入量.
表4 图书馆开放区域量化表
Tab.4 Quantification table of library open areas
表4 图书馆开放区域量化表
Tab.4 Quantification table of library open areas
由2.2节可知,室内人员数目的变化对建筑物能耗也具有影响.因此,将图书馆逐时室内人员数作为输入参数之一.
本研究主要针对图书馆建筑的能耗,因此输出参数为图书馆逐时能耗.
数据选择的时间范围从2020年7月13日到至2020年11月30日,剔除了个别缺失数据的部分.
综上所述,本研究中的输入层节点数为3,输出层节点数为1.
由于输入参数之间存在数量级和单位的不一致,为了去除差异,常用的方法就是对参数进行归一化处理,公式如下所示.
y=(x-xmin)/(xmax-xmin) (6)
式中:x代表原始样本数据; y为处理后的数据; xmax为样本数据最大值; xmax为样本数据最小值.
在模型构建中,需要设置训练集和测试集.因此,将归一化处理后的数据按照85%和15%的比例随机划分为两部分,分别作为训练集和测试集.
根据前文分析,已经得出相似日选取的特征向量,即图书馆开放策略x1、气温x2和室内人员x3,构建特征矩阵X={x1,x2,x3}.下面对三个因素的量化进行说明.
首先是图书馆开放情况,其量化如表5所示.该表根据图1与图2的内容,对数值进行了设定.此处量化过程为简化数据处理过程,忽略了夏季与冬季图书馆开放情况的细微差异.这种差异在整体上看非常小,很难对结果造成较大影响,因此选择忽略.
另一个因素为气温,使用日平均气温数据描述当日的气温.
最后是室内人员情况.使用门禁系统记录的室内人员出入数据对日总室内人员数进行计算.用日总室内人员数描述当日室内人员情况.
使用归一化处理消除特性指标间的数量级差异和量纲差异.
计算测试集与训练集的相似度,并对模糊相似矩阵进行聚类.使用系统聚类的方法将测试集对应的训练集分为相似日和非相似日.根据相似日从前一节划分的训练数据中筛选出相应数据作为模型真正的训练数据.
LM神经网络的隐含层层数和隐含层节点数不定.因此需要通过实验确定一个较为合适的数目.
由于本研究中的模型参数构成并不复杂,此类模型的隐含层层数的选取范围不应过大.因此,将其设定范围划定于1至3层.为选择最优设定值,对不同层数的模型进行实验,得到相应的迭代次数和均方误差(Mean Square Error,MSE)其实验结果如图4所示.为确保实验结果的可靠性,各模型的训练结果均为运行10次后的均值.
根据图4可知,使用2层隐含层与使用3层隐含层在迭代次数和准确性上表现较好.同时,考虑到模型的训练速度会随层数增加而下降,因此2层隐含层在此次模型中适用性更高.
隐含层节点数的范围一般可由经验公式获得.
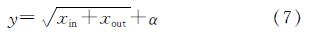
式中:y表示隐藏节点数; xin表示输入节点数; xout表示输出节点数,1<α<10.
输入参数数目为3,因此输入层节点数为3,输出参数为图书馆建筑的能耗,故输出节点数应为1.由经验公式可得隐含层节点数范围为3至12.为确保结果可信度,各相应模型均为10次训练后的均值,其结果如图5所示.由图5可知,隐含层节点为10模型最优.
为对能耗预测模型的性能进行评价,使用三种常用的预测模型评价指标.
平均绝对百分比误差(Mean Absolute Percentage Error,MAPE),其范围为[0,+∞),MAPE也大表示误差也越大,其公式如下.
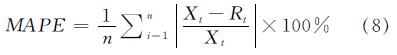
MSE大于0,通常,当MSE越接近0时,模型越好,其公式如下.
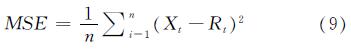
R2的范围为[0,1],一般情况下,R2越接近1时,模型的拟合程度越好,模型越完美.
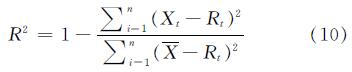
式中:n为预测样本数; Xt为第t个样本的真实能耗; Rt为第t个样本的预测能耗.
利用占数据总量15%的测试集对训练完成后的模型进行测试,将两种预测结果指标进行对比,如表5所示.从各项评价指标的对比可知,使用相似日法改进后,模型的准确程度有较为明显的提高.
为更清晰展示模型改进效果,用9月12日的结果作为例子,将两种模型的拟合度进行对比,如图6和图7所示.
图6 相似日LM神经网络模型拟合情况
Fig.6 The comparison of the fitting value of the optimized LM model and the true value
图7 普通LM神经网络模型拟合情况
Fig.7 The comparison of the fitting value of the general LM model and the true value
从拟合程度对比可知,普通LM神经网络预测结果中存在不少游离点,整体预测精度下降; 而改进后的模型预测结果中,基本没有偏差较大的游离点,预测曲线的拟合程度明显更优.
综上可知,使用相似日法进行改进的LM神经网络模型对于图书馆能耗的预测更加准确,大偏差游离点基本消失,预测曲线拟合程度更好.
针对高校图书馆能耗问题,使用LM神经网络模型进行预测,并使用相似日法改进模型.该相似日方法使用模糊聚类进行相似日选取.通过和普通LM神经网络预测模型结果的实验对比,证明改进后的预测模型可以更准确地对高校图书馆的能耗进行预测.更准确的预测模型不仅可为日后建筑综合能耗系统的研究提供有力的基础,同时也有利于节能策略研究工作的进一步发展.
本次研究主要聚焦于预测模型的改进,因此使用的能耗数据并未细化分类.若进一步针对不同区域及不同系统的特征,建立更加细致的模型,可对相关模型的适用性进行更多研究.