基金项目:十二五国家科技支撑课题合作单位基金资助项目(2011BAJ03B03-5)
第一作者:王 鑫(1996—),男,硕士,主要研究方向为综合能源系统.E-mail:xjd_wangxin@163.com 通信作者:李安桂(1963—),男,博士生导师,主要研究建筑通风空调气流组织、地下空气环境、太阳能建筑一体化等.E-mail:liangui@xauat.edu.cn
(1.西安建筑科技大学 建筑设备科学与工程学院,陕西 西安,710055; 2.太阳能利用工程技术研究所,中国电建集团西北勘测设计研究院有限公司,陕西 西安,710065)
(1.School of Building Services Science and Engineering, Xi'an Univ. of Arch. & Tech., Xi'an 710055, China; 2.Institute of Solar Engineering Technology, Northwest Engineering Corporation Limited, Power China, Xi'an 710065, China)
integrated energy system; load forecasting; construction model; error analysis
DOI: 10.15986/j.1006-7930.2022.05.015
在人类提高环保意识和改变能源结构的呼声中,能源互联网应运而生,为应对能源危机提供了新思路,成为学者研究重点[1].能源互联网主要通过互联网技术,将新能源利用技术、计算机信息技术与新型电力网络相结合,从而实现能量的双向流动[2].该技术改变了电力系统传统的发配输用四个环节,是当前应对能源问题和推动能源系统发生变革的重要方式,而综合能源系统能发挥载体作用,承载能源互联网进行能源整合和高效利用等工作[3].因此,研究综合能源系统对我国改变能源消费结构,提高能源利用效率以及可再生能源消费占比有重要意义.
国内外研究机构和高校在综合能源系统的计算模型与求解方法等研究上已取得大量的成果[4],但是对综合能源系统负荷预测的研究较少,多用负荷模拟软件模拟,这种方法得到的负荷偏差较大且不能用于动态预测,同时,在综合能源系统规划设计计算中,存在风电等清洁能源出力不确定性难题[5].预测风光资源特征量(风速和辐射照度)可以有效预测风光发电设备出力,因此研究预测技术对综合能源系统的规划设计计算以及削减风光发电设备出力不确定性有着重要意义.
负荷预测是综合能源系统设计、运行、控制的基础[6].关于预测方法,以往学者做了很多研究.文献[7]基于模糊理论与时间序列,提出了模糊时间序列方法负荷预测模型,在短期负荷预测上有较好的准确度.文献[8]根据我国20年间逐年的能源生产总量数据,运用ARMA(Autoregressive Moving Average Model,ARMA)模型对我国能源生产进行了预测,预测结果与我国能源生产情况趋势相同,证明了时间序列预测法适用性广泛的特点.文献[9]改进了Elman网络(global feed forward local recurrent,Elman),采用相关系数预处理和样本异常值平均化处理,将Elman网络的输入层变量大幅精简,减少了预测的时间并提高了预测精度.
近年来,大量的研究表明,建立优势互补的混合模型或改进模型能够提高预测的精度.文献[10]提出了由时间序列法和神经网络结合的混合模型,得到了很好的预测结果,并指出,混合模型相对于两个原模型,均方根误差降低了40%,文献[11]基于神经网络和模糊推理提出了新的混合预测模型,综合模型在预测短期负荷时,预测结果更贴合实际.文献[12]基于混沌理论和神经网络构建了混合模型,用混沌理论去优化神经网络,得到预测结果更好的混合模型.文献[13]结合遗传算法和神经网络构建了混合模型,用遗传算法优化人工神经网络相关参数,得到更好的参数设置,再用优化后的神经网络预测负荷,将平均百分比误差降低了2%~4%.文献[14]提出了一种改进的PSO-BP神经网络算法预测大型公共建筑的冷负荷.通过对输入变量与输出结果进行灰色关联度分析,确定影响冷负荷的关键性因素,将其作为输入变量,提高了预测结果的精确度,在算例中使用改进模型,将均方根误差从20%降低至7%.文献[15]提出一种基于相似日LM(Levenberg-Marquardt, LM)神经网络的高校图书馆能耗预测模型,改进后的预测模型与传统预测模型的各项指标进行对比分析.依据对比结果可知,改进后模型的平均绝对百分比误差降低了1.28%达到11%左右,改进模型预测精度有明显提升.
上述研究表明混合模型和改进模型相对于传统模型,通常可以降低一定的预测误差,在负荷预测研究中使用广泛.但是,负荷预测研究中,电负荷预测研究出现较早,热负荷、风光资源数据预测研究起步相对较晚[13].近年来,大量的综合能源系统已经部署完成或者正在部署中,综合能源系统所需要的负荷数据,包括园区热、冷、电、气负荷,且不乏有对风电出力有预测需求的系统,负荷的多样化使得实现综合园区综合能源系统动态管理的关键难题之一就是更通用的负荷预测技术,尤其是综合能源系统在管理时所需的短期负荷预测技术,且需有较好的适用性,能在没有历史运行数据或者运行数据较少时完成预测任务,并需要兼容多元负荷及风光资源特征量(风速和辐射照度)的预测.本文提出了一种新综合预测模型AMIRA-LSTM模型,融合了两种模型各自的优势; 并用算例验证模型在不同负荷类型、不同的训练集下的负荷预测以及风光资源数据预测上的准确性和兼容性.
ARIMA模型全称为移动差分自回归移动平均模型(Autoregressive Integrated Moving Average Model,ARIMA),是用于预测平稳时间序列的最受欢迎的线性回归模型之一[16],且有预测所需数据量较小的特点.LSTM网络全称为长短期记忆网络(Long-Short Term Memory,LSTM),是拥有强大处理非线性数据的模型 [17],它成功的解决了原始循环神经网络梯度消失的问题,能够很好地处理时间序列数据[18].受到这两种模型自身特点的启发,提出了ARIMA-LSTM综合预测模型.
ARIMA模型表示为ARIMA(p,d,q),其中参数p,d和q表示预测模型的结构,该模型可拆分为自回归AR(p),移动平均值MA(q)和差分度d.
AR(AutoRegressive,自回归模型)模型确定当前时间序列观测值,是先前时间序列观测值加上一些噪声项的线性组合.参数p为自回归模型的阶数.
MA(Moving Average,移动平均值)模型中,当前时间序列值是过去误差的函数.移动平均预测模型使用预测误差的误差值来改进当前的预测,参数q为移动平均的阶数.
I代表差分操作,它主要是对等周期间隔的数据进行线性求减.从而使数据变得平稳,ARIMA一般进行一次差分即可稳定,因此d一般取值为0、1、2.
ARIMA(p,d,q)的数学公式可以描述如下.
xi=α0+α1xi-1+α2xi-2+L+αpxi-p+
ε0+β1εi-1+β2εi-2+L+βqεi-q (1)
式中:αp,βq为时间序列的自相关系数.
模型的建立过程:构建ARIMA模型的一般过程涉及三个迭代步骤.
第一步为模型识别和选择模型类型.为了判断最佳拟合模型,固定时间序列必不可少,在该序列中,基本统计属性(例如均值,方差,协方差或自相关)随时间是恒定的.为了构建平稳时间序列,使用了适当的微分度(d).然后,检查自相关函数(ACF)和部分自相关函数(PACF)以选择模型类型;
第二步为参数估计.选择q和p的阶数,在ARIMA模型中,许多学者已经基于Akaikes信息标准(AIC)、最小描述长度(MDL)、贝叶斯信息标准(BIC)或模糊系统等开发了许多方法[19].在本文的研究中使用AIC指标来估计参数;
最后一步为对残值(εt)分析的诊断检查.通过一些诊断统计数据和残差图检查偏差,包括残差白噪声检验,及判断E(εt)是否为零,为零则代表模型通过检验,不同时刻的变量之间不相关,反正则相反,需要修正模型.
LSTM网络是递归神经网络(Recurrent Neural Network,RNN)的扩展.由于LSTM模型在处理大尺寸参数方面具有多功能性,并且在每一层中都使用了非线性激活函数,因此,LSTM模型可以捕获数据中的非线性趋势并长时间记住以前的信息.LSTM已成功应用于许多时间序列问题.LSTM结构的优点是它包含三种类型的门,包括输入,忘记和输出.如图1所示,LSTM解决了RNN消失的梯度问题,并允许长期存储信息.
LSTM单元(图1)的主要信息流可以用数学方式描述.符号+和×表示模型中的加法和乘法,箭头表示信息的流向.存储器门的第一层确定将不必要的信息删除到单元状态,可以表示如下.
ft=σ(Wf×xt+Uf×ht-1+bf) (2)
式中:ft表示在时间忘记门,σ表示sigmoid函数,Wf和Uf表示权重xt表示输入值,ht-1表示在时间t-1的输出值,并且bf表示偏差项.
第二个输入门根据当前输入向量决定应在单元状态下存储哪些信息.同时由tanh层生成新的状态值Ct.具体表达式如下.
it=σ(Wi×xt+Ui×ht-1+bi) (3)
C^-t=σ(Wc×xt+Uc×ht-1+bc) (4)
式中:it表示在时间t的输入阈值,Wi,Ui,Wc,和Uc是重量bc和bi是偏见.为了在时间t更新单元格的状态,表达式如下.
Ct=ft×Ct-1+it×C^-t (5)
第三输出门作为输出信息生成,可以表示如下.
Ot=σ(Wo×xt+Uo×ht-1+bo) (6)
式中:Ot表示在此时的输出值,Wo和Uo是权重,并且bo是偏差项.然后,该单元的输出值可以表示如下.
ht=Ot×tanh(Ct) (7)
式中:表示时间t单元的输出值,tanh表示激活函数,并且Ct表示在时间t的单元状态.数据通过三个门之后,将输出有效信息,并会忘记无效信息.
综合能源系统中的多元负荷数据及资源数据(风速和太阳日辐射量)为时间序列数据的形式,多元负荷数据均可假定由线性部分和非线性部分组成,ARIMA方法可以成功地建模时间序列数据中的线性关系,而LSTM可以成功地建模非线性分量.为了达到最佳的预测结果,本文构建了混合模型,如图2所示,它们结合了ARIMA和LSTM方法的优势.即ARIMA-LSTM预测模型,用公式可以表示为
Lp,t=Lap,t+Llp,t (8)
式中:Lp,t为综合预测序列; Lap,t为ARIMA模型预测序列; Llp,t为LSTM模型预测序列.
基于图2中提出的方法的工作流程.
综合模型建模流程可以分为以下几个步骤:
(1)通过数据采集等方法获取历史数据.
(2)平稳性检验,平稳的数据指其基本统计属性(例如均值,方差,协方差或自相关)随时间是恒定的.若数据不平稳,则需要进行差分运算.差分运算是将非平稳的时间序列进行平稳化的运算方法.如果1阶差分不能使序列达到平稳的话,本文还可以继续进行差分运算,直到将序列转换为平稳序列为止.差分公式如下.
1阶差分
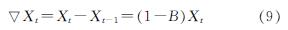
2阶差分
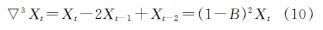
以此类推,可d阶差分为

式中: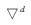 为d阶差分算子.
为d阶差分算子.
(3)模型定阶:
通过差分运算得到了ARIMA(p,d,q)模型中的其中一个参数d,接下来就要确定对参数p和q进行定阶,这里用到的定阶方法就是AIC准则,方法如下.
假设Xt为ARMA(p,q)模型,其中未知参数的个数为p+q+1个,其中包括自回归系数φ1,φ2,…,φp、移动平均系数θ1,θ2,…,θq和σ2ε,那么ARMA(p,q)的定阶准则为
选取适当的p和q,使得AIC值达到最小,AIC计算公式为[19]
AIC=nln(^overσ)2ε+2(p+q+1) (12)
式中:n为样本容量,(^overσ)2ε与p、q有关.
若当p=p',q=q'时,值最小,则认为模型的阶数为p'和q',即为ARMA(p',q')模型.
(4)ARIMA模型的线性预测.应用ARIMA统计模型提取生产时间序列的线性部分Lap,t,并计算拟合误差,这是下一步的输入项.设原始负荷数据集为H=[h1,h2,h3,…,hn],利用ARIMA模型得到H的历史数据拟合序列F和预测序列Lap,t.
F=[F1,F2,F3,…,Fn]
Lap,t=[Lap,1,Lap,2,Lap,3,…,Lap,n]
(5)将拟合序列F与相应负荷实际序列Hf相比较,得到拟合误差序列
ΔF=[ΔF1,ΔF2,ΔF3,…,ΔFn]
(6)LSTM建模的非线性预测.ARIMA模型的残差是LSTM机器学习模型的输入.因此,本文预测非线性数据计算公式为
Llp,t=f(ΔF1,ΔF2,ΔF3,…,ΔFn) (13)
式中:f(…)为LSTM的非线性建模.
(7)耦合和评估ARIMA-LSTM模型的最终结果.通过将ARIMA模型的预测结果与到LSTM网络的预测结果结合,可以获得拟合得出时间序列的最终结果.随后进行预测评价.
为了评估不同实验场景下的预测性能,选择科学的评估指标进行时间序列预测.作为评估指标常用的包括:均方根误差(RMSE),平均绝对误差(MAE),平均绝对百分比误差(MAPE)和相似度(Sim),这些指标用于评估不同模型在预测结果中的性能,并且可以表示如下.
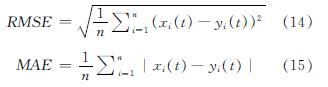
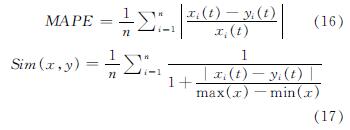
式中:xi(t)表示多元负荷数据值; yi(i)表示通过不同模型预测的产量值; n表示时间序列数.通常,RMSE,MAE和MAPE的值越低,预测任务的性能越好.此外,Sim值在[0,1]区间内,较高的Sim值表示较好的拟合结果.
本文使用某机场能源岛2019年全年8 760 h多元负荷数据以及资源数据集.包括热、冷、电、气负荷、风速、辐射照度等,如图3、图4所示.
其中,1月份数据作为样本数据,样本数据共有720小时的数据,用混合模型预测2月份负荷预测数据,与对比数据对比验证模型可靠性.本文在ARIMA模型中以样本数据(1月份数据)的前50%作为训练集,后50%作为测试集以确定最近模型.在LSTM网络模型中,以确定的ARIMA模型对样本数据的拟合产生的拟合误差(1月份拟合误差)的前50%作为训练集,后50%作为测试集训练最佳模型.
这里以热负荷预测为例,余同.
(1)平稳性检验,检验数据平稳性.热、冷、电样本均值及方差随时间变化均近似趋近于某定值,认为数据平稳,可以建模.而风速数据不平稳,作一阶差分后平稳;
(2)模型定阶,计算使用公式(12)计算最小AIC值,为了节约计算时间,使用编程计算方便节约时间,本文使用Python编程计算.经计算,当p=3,d=0,q=24时,AIC值最小,故时间序列模型确定为ARIMA(3,0,24);
(3)ARIMA模型计算
用确定好的ARIMA模型直接预测能源岛2月份1日到7日的负荷数据,得到能源岛2月份的线性预测负荷Lap,t,并与实际热负荷做对比,如图5所示;
(4)确定ARIMA模型后即可得到拟合误差序列,以拟合误差序列的前50%作为训练集,后50%作为测试集训练最佳LSTM模型.
在多次试验中,训练LSTM神经网络时,本文设置的初始学习率为0.005并且训练125次后学习率下降,衰落因子为0.2时,网格效果最好.图6显示了LSTM网络的训练过程.可以看出,在最后一次迭代完成后,RSME和Loss基本不再变动并且与0非常接近,认为模型已经训练完成.其中,不同的数据集要设置不同的学习率.
用训练好的模型预测2月份负荷,得到2月份的非线性预测负荷Llp,t.
(5)用公式(8)得到ARIMA-LSTM模型综合预测序列Lp,t,至此,热负荷综合预测完成.用同样的方法的得到电负荷、风速预测序列(冷负荷为零).
将模型综合预测结果与对比数据进行对比,如图7所示,其中,热负荷、电负荷和风速数据均为2月1日到7日的逐小时数据.
为比较不同模型的预测效果,本文采用ARIMA 模型、LSTM 模型、Elman模型[9]与ARIMA-LSTM 组合模型,分别对该能源岛2月1日至7日为期一周的热电负荷及风速进行逐时预测,并计算日相对平均误差MAPE.各模型的预测结果误差曲线如图8所示.
由图8可知,电负荷的预测效果相对较为理想,热负荷和风速由于其本身的特点误差相对更大,但基本控制在一定范围内.同时,相对于其他模型,本文的混合模型在大多数情况下相对平均误差MAPE更小,预测效果最理想,而ARIMA模型的预测效果在这几种方法中效果最不理想.组合模型相比于其他三种模型在负荷预测方面表现得更出色.
为了比较训练集对预测结果的影响,以一种负荷为例,测试了训练集为一周、一月、一年所得预测结果的误差,如下表所示.
表1 不同模型在不同训练集长度下对应的热负荷预测误差
Tab.1 Thermal load prediction errors corresponding to different models under different training set lengths
根据表1分析可知.LSTM模型作为当下比较流行的模型[17],其预测精度高、仅需历史数据即可进行预测的特点受到极大的关注.而本文建立的ARIMA-LSTM组合模型,不仅有相比LSTM模型更好地预测精度,同时保证了运算时长相差不大; 而且该模型在训练集更少时将更可靠.
本文基于ARIMA以及LSTM网络构建了用于综合能源系统多元负荷预测及风光资源数据预测的ARIMA-LSTM混合模型,介绍了模型的建模过程以及运算流程.
该模型结合了线性预测和非线性预测,能更充分的提取历史数据的规律,能有效的减少预测误差,削减风光等设备由于出力不确定性造成的负面影响.
该模型在训练集较少时预测表现更加可靠,同时计算时间能控制在合理的范围内,对综合能源系统在运行初期的调控计算分析有更好的适用性.