基金项目:国家自然科学基金(52078408、U20A20311); 陕西省杰出青年基金项目(2020JC-43)
第一作者:高 阳(1996-),女,硕士生,主要研究太阳能供暖集蓄热系统设计方面研究.E-mail:1298938497@qq.com 通信作者:王登甲(1984-),男,博士,教授,主要从事可再生能源供暖领域的研究.E-mail:wangdengjia@xauat.edu.cn
(1.西部绿色建筑国家重点实验室,陕西 西安,710055; 2.西安建筑科技大学 建筑设备科学与工程学院,陕西 西安,710055)
(1.State Key Laboratory of Green Building in Western China, Xi'an 710055,China; 2.School of Building Services Science and Engineering, Xi'an Univ. of Arch. & Tech., Xi'an 710055, China)
solar heating; collection system; solar fraction; heat storage systom; matching method
DOI: 10.15986/j.1006-7930.2022.06.020
我国西北及高原地区太阳能资源丰富,以太阳能替代或部分替代常规能源供暖是降低一次能源消耗的有效技术途径[1].目前,对于太阳能供暖系统的设计方法主要有平均参数法、图表公式法及仿真模拟法等方法.
平均参数法是一种稳态计算方法,以集热器效率方程为基础,利用气象参数平均工况计算集热系统年平均效率,弱化了动态参数在设计过程中对系统效果的影响,例如国家标准《太阳能供暖工程技术规范》GB50495—2019其设计过程是先计算集热器面积,再根据推荐范围确定蓄热容量,最终确定太阳能系统规模.图表公式法将系统测试或数值模拟的结果整理成可供查看的图表或直接使用的计算公式,作为太阳能供暖系统的设计工具,其核心是以图形和方程的形式展示的太阳能供暖系统无量纲变量和性能的关系,如F-chart是图表公式法的典型应用,该方法主要考虑了集热面积对于系统性能的影响[6].仿真模拟法[7]是一种动态计算方法,主要用于集热系统面积、蓄热容积、辅助加热规模等系统优化匹配研究,通过设置目标函数,经过系统优化算法计算得到满足目标函数的自变量,该方法准确度较高,但是需要使用者具有扎实的软件基础,因此,该方法很难直接应用于工程设计和推广.
综上所述,不同的太阳能供暖系统设计方法具有不同的适用条件.本文在上述研究方法的基础上,利用模拟软件TRNSYS建立太阳能供暖系统动态模型,模拟得到不同设备容量参数下的太阳能供暖系统性能,探究太阳能供暖系统设备容量关联关系.确定出太阳能供暖集热、蓄热系统设备容量相互影响关系,给出两者同时确定方法,提出了太阳能资源不同地区主要城市的设计参数推荐范围,为太阳能供暖系统在工程上的准确设计提供指导作用.
太阳能供暖系统的原理[13]如图1所示,系统主要由太阳能集热、蓄热系统、辅助热源系统及末端用户等构成,本研究内辅助热源采用电加热.集热循环泵P1采用温差控制法,蓄热循环泵P2采用温度控制法,启闭条件如表1所示:
表1 集热系统循环泵P1、P2启闭控制
Tab.1 Circulating pump P1, P2 open and close control
辅助热源的启闭条件如表2所示.
上述系统,热量平衡方程如公式(1)所示.
∫qsolardt+∫qauxdt=∫qloaddt+∫qlossdt+∫Δqtankdt (1)
式中:qsolar为集热器有效集热量,kW; qaux为辅助热源加热量,kW; qload为用户热负荷,kW; qloss为系统热量损失,包括集热系统热损失、蓄热水箱热损失和管道热损失,kW; Δqtank为蓄热水箱瞬时蓄热量,kW.
太阳能集热系统瞬时集热量qsolar用公式(2)表示为
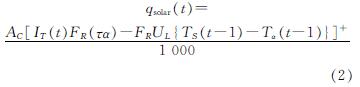
式中:AC为集热器面积,m2; +表示只有当集热量为正时,来自集热器的热量才会传递给水箱; IT为入射到集热器倾斜表面的总太阳辐射强度,W/m2; FR(τα)为集热器的性能系数; UL为集热器热损失系数,W/m2·K; Ta为环境温度,℃.
蓄热水箱和辅助热源提供给末端的热量由式(3)和(4)计算.如果蓄热水箱供水温度高于末端供水管所需最低供暖温度时,则末端用户完全由蓄热水箱提供热量,辅助热源不开启; 否则,开启辅助热源,由辅助热源加热到所需供暖温度后再提供给末端.
TS(t-1)≥TS,Min时,qload(t)=qtan,k,s(t) (3)
TS(t-1)<TS,Min时,qload(t)=qaux(t)+qtank,s(t) (4)
式中:TS为蓄热水箱供水温度,℃; T(S,Min)为末端供暖所需最低温度,℃; qtank,s为蓄热水箱提供给末端的热量,kW.
随着太阳能集热量的增加,储热水箱中储存的热量积累,其热损失量也随之增加,储热水箱损失的热量可通过式(5)和(6)计算,即
qloss(t)=USAS([TS(t-1)-Tα(t-1)])/(1 000) (5)
AS=1.845(2+h/d)V2/3 (6)
式中:US为水箱的热损失系数,W/m2·K; AS为水箱的表面积m2; h/d为圆柱形储罐的高径比; VS为蓄热水箱容积,m3.
供暖期蓄热水箱瞬时蓄热量Δqtank可通过式(7)来确定,即
Δqtank(t)=qsolar(t)-qtank,s(t)-qloss(t) (7)
太阳能供暖系统年累计集热量Qsolar,kW·h; 通过蓄热水箱提供给末端的总能量Qtank,s,kW·h; 总辅助加热量Qaux,kW·h; 可以用式(8)~(10)表示.
Qsolar=∑qsolar(t) (8)
Qtank,s=∑qtank,s(t) (9)
Qaux=Qload-Qtank,s=∑qaux(t) (10)
依据前述数学关系指导建立该系统的动态仿真模型[10],如图2所示.
太阳能具有不稳定的特点,通常为了提高太阳能保证率,往往需要增大系统设备容量,初投资相应增大,初投资高是阻碍太阳能供暖系统推广的主要原因之一.因此,合理的设计方法应能在保证系统节能性的前提下,提高其经济性能.
采用均热成本Levelized Cost of Heat(LCOH)对经济性进行评价,根据多数地区太阳能系统施工实际情况,不考虑政府补贴与土地租金,系统生命周期内每产生1 kW·h能量的成本由系统初投资,运行和维护费用及系统总供暖量构成,可以表示为[5]
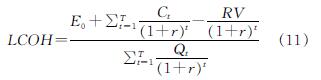
式中:E0为整个系统的初投资,CNY; Ct为第t年运行与维护总费用,CNY; RV为系统的剩余价值,CNY; Qt为系统第t年放热量,kW·h; r为折现率,%.
式(11)中,太阳能供暖系统初投资E0主要包括太阳能集热场、蓄热水箱、辅助热源三大部分[8].则E0可以表示为
E0=Ecoll+Eaux+Ev (12)
式中:Ecoll,Eaux与Ev分别为集热场、辅助热源与蓄热水箱的初投资,CNY.
太阳能集热场初投资Ecoll可以由集热器面积AC(m2)来计算[9].
Ecoll=500(1-1.652·10-5AC+2.26·10-10A2C-5.738·10-16A3C) (13)
蓄热水箱初投资与其容积相关,初投资可以表示为
Ev=pv·Vs (14)
式中:Vs为蓄热容量,m3; pv为单位蓄热容积的价格,一般[5]取138 CNY/m3.
辅助热源容量需满足供暖季最大热负荷,因此辅助热源初投资Eaux可以表示为
Eaux=C·pc (15)
式中:C为辅助热源容量,kW; pc为单位容量辅助热源的价格,CNY/ kW.
系统的维护费用取初投资的1%,运行费用cr可以表示为
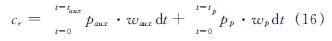
式中:paux为辅助热源单位功率使用价格,CNY/kW; waux为辅助热源功率,kW; pp为电价,CNY/kW; wp为水泵运行功率,kW.
太阳能保证率是评价太阳能供暖系统设计优劣的重要指标,表示由太阳能提供的热量占所需总热量的百分比,可由公式(17)表示[12].
F=(Qsolar)/(Qload)=(Qcoll-Qloss)/(Qload)=(Qcoll)/(Qload)-(Qloss)/(Qload) (17)
式中:Qsolar为供暖期内系统总供热量, kW·h; Qload为供暖期内建筑总热负荷,kW·h; Qcoll为供暖期内系统总集热量,kW·h; Qloss为供暖期内系统总热损失,kW·h.
从式(17)来看,太阳能保证率大小主要与两个无量纲参数密切相关,第一个是与太阳能供暖系统的增益有关,第二个是与系统的热损失有关.分别用X和Y代表,即公式(18)和(19).
无量纲参数X,即系统热损失与建筑热负荷的比值.
X=Qloss/Qload (18)
无量纲参数Y,即系统集热量与建筑热负荷的比值.
Y=Qcoll/Qload (19)
基于此,下面针对无量纲参数X、Y及太阳能保证率F三者间的关系进行分析.
以拉萨地区为例,随机选取多种建筑面积条件下的供暖热负荷(热负荷1~6),改变设备容量进行多次模拟,将模拟结果进行无量纲化处理,结果发现,工况各不相同的太阳能供暖系统其无量纲参数X、Y与系统太阳能保证率F表现出良好的一致性,结果如图3和4所示.
图3 太阳能保证率F随无量纲参数X的变化趋势
Fig.3 Variation trend of solar guarantee rate F with dimensionless parameter X
图4 太阳能保证率F随无量纲参数Y的变化趋势
Fig.4 Variation trend of solar guarantee rate F with dimensionless parameter Y
图3表示,对于同一地区,太阳能保证率F与无量纲参数X、Y构成三维空间中的一条曲线,采用回归分析的方法表示该曲线如式(20)所示.
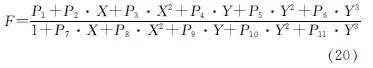
式中:X为系统热损失与热负荷的比值; Y为系统集热量与热负荷的比值; P为回归系数,如表3所示.
以相关系数R2来评价回归模型,评价指标为式(21)[13].
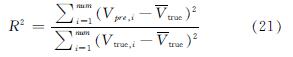
式中:Vtrue,i为动态模拟得到的太阳能保证率值; Vpre,i为该设计方法计算得到的太阳能保证率值; V^-true,i为动态模拟得到的太阳能保证率平均值.
针对太阳能资源不同区域,以拉萨、西宁、西安为例[9],对回归方程进行评价,如表4所示.表中各地区回归模型R2为0.95~0.97之间,表明所选变量集热器面积、蓄热水箱与太阳能保证率相关性较好.
对于供暖期动态室外气象条件,为方便工程计算,采用平均参数法来近似替代动态模拟结果.以下对平均参数法与动态模拟法的所得结果一致性进行了证明.
太阳能供暖系统集热量可用式(22)进行计算.
Qcollection=a·A·G·η0·τ (22)
式中:Qcollection为计算得到的供暖期系统集热量,kWh; a为单个太阳能集热器有效集热面积与总面积的比值; G为水平面12月的月平均时刻辐照量,kW/m2; η0为集热器的效率参数; τ为供暖时长,h.
太阳能供暖系统的热损失Qloss主要由集热系统热损失Qloss1、蓄热系统热损失Qloss2和管网热损失Qloss3三部分的热损失组成.
集热系统热损失为
Qloss1=(A·FR·UL·(Tref-Ta))/(1 000)·τ (23)
蓄热系统热损失为
Qloss2=Utank·AS·(Ts-Ta)·τ (24)
AS=1.845·(2+h/d)·V2/3 (25)
管网热损失为
Qloss3=m·Qcollection (26)
式中:Qloss1为集热系统总热损失,kW·h; FR为集热器换热器效率系数; UL为集热器热损失系数,W/m2·K; Tref为供暖期内集热器内的平均温度,℃; Utank为蓄热水箱热损失系数,W/m2·K; Ta为计算采暖期室外平均温度,℃; Qloss2为蓄热系统总热损失,kW·h; AS为蓄热水箱的表面积,m2; h/d为蓄热水箱的高径比; VS为蓄热水箱容积,m3; Qloss3为管网总热损失,kW·h; m为管网热损失率,取0.2[2].
将回归值与模拟值进行对比,如图5、6所示.并求两者平均值,系统集热比均值为0.856,系统热损失比均值在1.246,因此,可采用平均参数计算的方法近似替代动态系统模拟输出的系统性能参数.
上述公式(20)是关于太阳能保证率F与集热面积Ac和蓄热容积Vs构成的是二元隐式方程式,需转化为一元方程后方可求解.因此,引入集蓄热比VS/AC,可将上述方程式转化为仅含有集热面积Ac作为未知数的一元方程进行求解[2,12].以下将给出典型城市集蓄热比VS/AC和基于经济性的太阳能保证率F的推荐范围.
以拉萨地区为例,依据前述建筑热负荷1~4,计算出不同设计太阳能保证率下的系统均热成本LCOH,如图7所示.
从图7中可看出,对于同一系统,太阳能保证率在60%~80%的时候,系统的均热成本最低,这是因为太阳能供暖系统具有初投资高运行费用低的特点,当太阳能保证率低于60%(f1),太阳能供暖带来的节能效果小于初投资所占的费用; 而当太阳能保证率大于80%(f2)时,由于极端天气的存在,增加太阳能保证率就意味着增大设备容量即更高的初投资,因此,在拉萨地区太阳能供暖系统设计过程中,太阳能保证率选择60%~80%更经济.
采用同样的方法,可得各个太阳能资源不同地区典型城市的太阳能供暖系统设计推荐值如表5所示.
对模拟结果分析发现,不同集蓄热容量组合可实现相同的太阳能保证率,对比它们的均热成本如图8所示.
可以看出,随着Vs/Ac的增加,不同工况下的太阳能供暖系统均热成本LCOH都呈现先剧烈后缓慢的减小趋势.该变化过程可分为三个阶段,首先,集蓄热比值很小时,系统几乎不蓄热,为达到供暖要求需增大集热面积,系统均热成本较高; 紧接着,随着集蓄热比值增加,集热面积可适当减小,系统均热成本明显降低; 最后,因为太阳能保证率一定时,集热面积的取值范围也一定,再增大集蓄热比值,即增大蓄热容积,其初投资增加对系统均热成本影响较小,故而均热成本呈现平缓趋势.综合考虑经济与节能性,在拉萨地区太阳能供暖系统的设计过程中,推荐Vs/Ac的比值为0.15~0.25.
采用同样的方法,可得各个太阳能资源不同地区典型城市的太阳能供暖系统设计推荐值如表5所示.
现采用本研究的集蓄热简化设计方法与规范设计方法对比分析太阳能保证率和系统经济性.选择拉萨市某办公建筑(建筑面积3 700 m2,采暖期11.15~3.15)为分析对象.
分别采用规范推荐方法(先计算集热面积再确定蓄热容积,用M表示)及本设计方法(解方程同时获得集、蓄热设备参数,用N表示)得到该系统的集蓄热设备参数,比较两者实际太阳能保证率F和均热成本LCOH的大小,如图9所示.
从图9中可以看出,规范方法得到的太阳能保证率偏差范围在3%~14%,且设计保证率越高,太阳能供暖系统的实际保证率与设计保证率偏差越大; 而采用本设计方法得到的太阳能保证率偏差范围在2%~8%,与规范设计方法得到的太阳能保证率偏差相比波动范围更小,同时所对应的LCOH普遍低于规范方法.因为相较于现有规范提出的先计算集热器面积再根据推荐范围确定蓄热容积,本研究提出的设计方法考虑到了集蓄热系统间协同作用对于太阳能保证率和系统经济性的影响,设计方法中包含参数更加全面,推荐值范围更加明确.
通过仿真软件TRNSYS编制了太阳能供暖系统动态模型,基于大量的模拟结果,归纳总结出了太阳能供暖系统集热量、系统热损失、建筑热负荷和太阳能保证率间的内在联系,并进一步分析了系统设备容量与系统经济性和节能性的关系,得到结论如下:
(1)本研究提出无量纲参数X表示系统热损失与建筑热负荷之间的关系,无量纲参数Y表示系统集热量与建筑热负荷之间的关系,通过回归分析的方式建立无量纲参数X、Y和太阳能保证率F间的数学关系,确定了太阳能供暖系统在不同工况下都具有的共同特性,为简化设计方法的提出奠定了理论基础;
(2)以太阳能保证率F作为评价系统节能性的主要指标,以太阳能供暖系统全生命周期内的均热成本作为评价系统经济性的主要指标,基于大量的模拟结果,给出了不同太阳能资源地区的参数推荐范围,在此推荐范围内,可通过计算得到最佳系统设备参数(集热面积和蓄热容量),使得系统均热成本最小;
(3)本研究给出了太阳能集热面积和蓄热容积更为明确的配比范围,提出了太阳能集热面积和蓄热容积两部分的简化配比设计方法,为太阳能供暖系统工程设计应用提供指导作用.