基金项目:国家自然科学基金资助项目(51979225; 51679199)
第一作者:党发宁(1962—),男,教授、博导,主要从事岩土工程数值分析、计算力学等方面的教学与研究工作.E-mail: dangfn@mail.xaut.edu.cn 通信作者:王海洋(1996—),男,硕士生、主要从事基坑数值模拟研究.E-mail:610146338@qq.com
(1.西安理工大学 西北旱区生态水利国家重点实验室,陕西 西安 710048; 2.中铁第一勘察设计院集团有限公司,陕西 西安 710043; 3.陕西建工第九建设集团有限公司,陕西 榆林 719000)
(1.State Key Laboratory of Eco-hydraulics in Northwest Arid Region, Xi'an University of Technology, Xi'an 710048, China; 2.China Railway First Survey and Design Institute Group Co., Ltd., Xi'an 710043, China; 3.Shaanxi Construction Ninth Construction Group Co., Ltd.,Shaanxi Yulin, 719000,China)
fine sand foundation pit; creep model; creep parameters; extended service
DOI: 10.15986/j.1006-7930.2023.01.006
我国西北地区存在大量粉细砂深基坑工程,随着城市化建设的快速发展,地下空间开发规模不断扩大,出现了越来越多有关粉细砂土的蠕变现象[1-4],粉细砂土地区深基坑工程施工具有显著的时间效应[5-8].工程建设期间由于各种原因,部分基坑工程在支护体系施工完成、土方开挖到一定深度后施工工期严重滞后,由此形成超期服役粉细砂深基坑.由于粉细砂土的强度低,施工扰动对地基土力学性能影响较大,因此,超期服役大型粉细砂深基坑工程具有更大的危险性,随着基坑开挖深度的增大,砂土的蠕变特性使护坡桩的变形也不断增大,施工停止过程过长就可能导致基坑工程事故的发生[9-10].
大型建筑物的长期沉降、基坑开挖临空面长期暴露引起的位移变形等都是目前工程中的蠕变问题,梅涛涛[11]对某港口码头进行研究,发现砂土地基在长期时间作用下会发生沉降变形,给地基的施工处理带来了影响.陈阳、廖庄等[12-13]对某砂土地区基坑的位移变形进行监测,发现在基坑开挖施工过程中桩顶、桩体位移和周边土体沉降会随开挖深度和时间发生变化.杨瑞意[14]在分析开挖后长期暴露的基坑变形特点的基础上,建立GM-BP神经网格模型,科学预测基坑后期的变形范围,以此判断基坑未来保持安全状态的时长.高洲、刘国彬等[15-16]依托某深厚淤泥层基坑,考虑其变形时间效应,利用三轴蠕变仪对土体进行卸载蠕变试验,引入能表达淤泥应力、应变以及时间之间关系的经验本构模型,并用于实际模拟,计算并分析淤泥基坑开挖暴露时的变形规律.Syiril Erwin[17]认为在研究基坑变形时需要考虑时间影响,采用数值模拟软件PLAXIS研究分析软土深基坑的时变特性,建立相应的软土蠕变模型,科学模拟随时间变化的墙体变形和地表沉降.葛海芳[18]结合某地铁站基坑开挖工程,考虑其时间效应,建立相应数值模型,引入指数蠕变法则,计算分析地层蠕变效应下,基坑随着时间变化过程,预测基坑延迟支护时对自身以及周边稳定的影响,为工程提供参考.
综上所述,目前,对基坑开挖过程中土体蠕变变形研究虽有不少,但都没有考虑到超期服役情况下粉细砂土体的蠕变变形.在实际基坑开挖中,开挖后长期暴露的粉细砂深基坑护坡桩存在侧向变形超标,桩前、后土体应力松弛,影响邻近基坑的道路与建筑的安全.因此,开展粉细砂深基坑超期服役时的蠕变变形对基坑稳定性影响研究是十分重要的.
经典的土体弹性、弹塑性模型无法反应基坑施工的时间效应,所以有必要采用合适的塑性与蠕变耦合的模型,对砂土地区基坑施工过程以及停工超期服役时的变形进行模拟计算及预测分析.本文首先确立适宜粉细砂土的时间硬化蠕变模型,根据砂土层蠕变试验结果对蠕变参数进行拟合.依托某大型粉细砂深基坑工程建立有限元计算模型,利用护坡桩侧向变形监测数据通过反分析调整蠕变参数,使计算结果更加贴近实际值.模拟计算了粉细砂场地大型基坑工程的施工过程,重点分析了超期服役对基坑土体变形的影响.最终实现对超期使用基坑变形随时间变化的预测.
陕北某市博物馆、图书馆和展览馆“三馆项目”场址原为明珠广场工程,在2013年已进行开发建设,场地的东部、北部、西部已全部进行了支护,支护结构设计安全有效期限为18个月.到2018年三馆项目基坑施工时,基坑支护体的运行环境已经超期服役5 a,早已超出支护结构设计的安全有效期限,给新工程的地质勘察、基坑支护、地基承载力设计、桩基施工带来很多困难.
据钻孔揭露,勘察深度范围内场地地层自上而下主要由少量杂填土、粉细砂以及粉质黏土等砂类土组成.此场地的砂土具有蠕变特性,超期服役会给基坑带来极为不利的影响.首先,基坑长期暴露引起坑底较大的回弹变形,降低了护坡桩前土的抗剪强度.其次,桩后土体应力松弛,增加护坡桩的下滑力,桩后土体失水干缩,抗滑强度降低.再次,长期暴露的粉细砂深基坑护坡桩侧向变形超标,喷护层脱落空鼓,桩间土流失,支护体结构强度降低等.这些均影响临近基坑的道路与建筑安全.因此,超期服役会对基坑的安全产生重要的影响.
为了对三馆项目粉细砂深基坑超期服役时的变形情况展开研究,需利用一种土体蠕变本构模型来描述基坑土体的应力、应变、时间之间的关系,既可以反映出粉细砂土的蠕变特性,又能应用于三馆项目等实际基坑开挖工程中.在蠕变模型的发展过程中,学者通过对土体的力学理论推导或蠕变试验,针对不同土体提出了许多蠕变模型,主要分为元件模型和经验模型[19].本文采用ABAQUS软件中的时间硬化蠕变模型来模拟计算粉细砂深基坑超期服役时变形情况,该模型能较好地反应土体的非线性特性,而且所需的参数较少,相对较简单[20].时间硬化函数可以表示为

式中: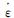 为等效蠕变应变率; σ为等效偏应力.以上公式对时间t求积分得
为等效蠕变应变率; σ为等效偏应力.以上公式对时间t求积分得
ε=1/(m+1)A(σ)ntm+1(2)
将上式左右两端取对数形式,得
lnε=lnA/(m+1)+nlnσ+(m+1)lnt(3)
下文引用文献[21]中粉细砂土的室内三轴蠕变试验曲线,对公式(3)中的A、m、n三个参数进行拟合,确定出粉细砂土的蠕变参数.范厚彬[21]对某粉细砂场地进行勘察钻孔,将钻孔中的粉细砂土作为三轴蠕变试验的土样,粉细砂土的物理力学性能指标如表1.
试验仪器采用三轴蠕变试验仪.有5个试样,由于开采的土样为受扰动土,因此,它的受力状态与地层原始位置的受力状态存在差异.为了克服这一误差,所以,在进行三轴蠕变试验前需要对土样进行预压,然后再进行加载,试验采用分级加载,即在5个相同侧压力均为90 kPa围压试验基础上.分别对5个试样施加不同的竖向载荷.加载情况如表2,试验时间设置为5 d.
序号 围压σ3/kPa 轴向力σ1/kPa 偏应力(σ1-σ3)/kPa1 90 106.7 17.72 90 124.5 35.53 90 136.3 47.34 90 148.1 59.15 90 168.3 79.3
图1是5个试样在90 kPa围压下三轴蠕变全过程试验曲线图,从图中可看出砂土的蠕变变形随着应力水平的增大而增大,整体为衰减蠕变.
图1 90 kPa围压土样的三轴蠕变全过程试验曲线
Fig.1 Triaxial creep test curve of soil samples under 90 kPa confining pressure
做出围压为90 kPa下的lnε~lnt曲线,将曲线线性拟合为直线,如图2所示.
由公式(3)可得直线斜率K=m+1.从图2 拟合直线中,可以得出在轴向应力分别为106.7 kPa、124.5 kPa、136.3 kPa、148.1 kPa以及168.3 kPa下拟合直线的斜率K分别是0.307 7、0.142 1、0.156 7、0.134 0、0.098 9.对上述斜率求取平均值得m+1= 0.167 9,m=-0.832 1.
同理,做出围压为90 KPa下的lnσ~lnε曲线,并将曲线线性拟合为直线,如图3所示.图3中横坐标为不同偏应力下的对数值.
由图3中lnσ~lnε拟合直线的斜率可知公式(3)中的参数k=n,在蠕变时间分别为3 585 min、4 301 min、6 468 min、5 021 min以及7 149 min下拟合直线的斜率分别是2.153、2.146、2.098、2.081、2.054,求取平均值得n=2.106.
将上文计算的m、n代入公式(1),再利用图1可拟合出A=1.583 99×10-14.则90 kPa围压下粉细砂土的蠕变应变率方程为

三馆项目采用了三种基坑支护设计方法,分别是Ⅰ型护坡桩、Ⅱ型护坡桩以及Ⅲ型护坡桩,由于Ⅲ型护坡桩是最危险工况,本文建立有限元三维计算模型,考虑土体蠕变特性,对三馆项目粉细砂深基坑Ⅲ型护坡桩进行蠕变模拟.
选取Ⅲ型护坡桩剖面地段建立计算模型,模型尺寸参考三馆项目工程并加以简化,尺寸为85 m×67 m× 35 m,基坑设计开挖深度为16.66 m,地下水位于地表以下20.50~25.50 m处.计算模型图如图4所示,采用桩径为0.8 m,净距为1.5 m的护坡桩,桩长为30 m.在距离桩顶为4.5 m、8.5 m、12.5 m处设置三排抗拉锚索,锚索长为18 m,锚固段长度为12 m,自由端为6 m.冠梁高度为0.9 m,宽度0.6 m.
三馆项目基坑支护结构采用护坡桩与冠梁、锚索结合支护形式,其中,支护结构设计参数如表3~表4所示,有限元ABAQUS中线弹性本构参数主要是弹性模量E和泊松比μ,其中,支护结构中冠梁、护坡桩及锚索的强度参数如表5所示.架设锚索时施加450 kN的预应力,使用降温法模拟锚索预应力的施加,锚索的膨胀系数为1.2×10-5.
ABAQUS在Drucker-Prager模型中加入了时间硬化蠕变模型,不用再通过子程序进行定义.当同时激活蠕变和Drucker-Prager塑性模型,ABAQUS可以自动进行耦合计算.
所以本文采用Drucker -Prager模型基础上的时间硬化蠕变模型对地基土层进行蠕变定义.其中地基土层分为3层:分别为杂填土、粉质黏土以及粉细砂,土层的力学参数见表6.
土体蠕变参数取上文确定参数,为A=1.583 99×10-14, m=-0.832 1,n=2.106.
建立三维计算模型,土体、冠梁以及护坡桩等均采用三维实体单元C3D8(8节点六面体单元).锚索采用T3D2单元(2节点桁架单元),网格划分如图5.
计算的边界条件为,在有限元模型底部施加全约束,四周施加法向约束,模型顶部是荷载边界,基坑外地面荷载为15 kPa,支护体系剖面图如图6所示.
按照三馆项目工程现场的施工规划,基坑开挖施工工序如下:(1)护坡桩、冠梁浇筑施工;(2)开挖第一层土至深度4.5 m;(3)架设第一道锚索、喷射混凝土;(4)开挖第二层土至深度8.5 m;(5)架设第二道锚索、喷射混凝土;(6)开挖第三层土至深度12.5 m;(7)架设第三道锚索、喷射混凝土;(8)开挖第四层土至深度16.7 m;(9)喷射混凝土;(10)停工56个月.
为了分析基坑土体蠕变变形随基坑暴露时间的变化,选取了长边方向某一截面护坡桩桩身以及桩后土体表面的10个特征点进行研究,其中1、2、3、4和5号点距离桩顶分别为1 m、5 m、16 m、24 m、31 m,6、7、8、9和10号点距离基坑边界分别为4 m、13 m、23 m、30 m、45 m,如图7所示.
图8为基坑长边方向剖面以及基坑整体土体不同时刻水平侧向位移云图,其中“-”号表示向坑内方向变形.可知,桩后土体由于蠕变效应,其侧向变形在基坑开挖完成后增加明显,从开挖完毕停止施工,5 a时间内,桩后粉细砂土水平位移最大值从15.9 mm增加到40.8 mm,最大变形位置在开挖面附近. 通过对图9、10分析可知,处于护坡桩中部的2、3、4号点水平蠕变量较大.其中位于开挖面附近的特征点3号蠕变量最大,最大值达到22.5 mm,其蠕变速率减小的最慢.桩顶和桩底附近的1、5号点变形较小,3 a蠕变量不到14 mm,由图9可看出桩后不同位置点的水平蠕变变形速率基本都在两个月左右趋于平稳.
图8 不同时间基坑土体水平位移云图(单位:m)
Fig.8 Horizontal displacement cloud diagram of foundation pit soil at different times
图9 各特征点水平蠕变变形随时间变化曲线
Fig.9 Curve of horizontal creep deformation at each characteristic point with time
基坑桩后土体各特征点位置不同,其蠕变变形值、蠕变速率也有所差别.取变形最大值3号点以及较小值1号点进行分析.护坡桩桩顶附近的特征点1在前三个月内的平均水平蠕变速率为0.125 mm/d,一年内的平均水平蠕变速率为0.035 mm/d.开挖面附近的特征点3在前三个月的平均水平蠕变速率为0.213 mm/d,一年内的平均水平蠕变速率为0.058 mm/d.在同一时刻,基坑开挖面附近水平蠕变量以及蠕变速率较大,桩顶附近的水平蠕变量和蠕变速率较小.以0.1 mm/d作为蠕变稳定标准,特征点在1a内变形基本达到稳定.
以基坑长边方向为算例,研究护坡桩随着基坑停止施工变形趋势,图 11为护坡桩水平位移变化曲线:
由图 11可知,在基坑开挖完毕后,护坡桩会出现向坑内方向水平位移变形,并且位移随着时间的发展不断增大,最大变形在桩体中下部位置处,这是由于随着开挖的进行,锚索的架设可以有效限制桩身上部的侧向位移,对桩身整体侧向位移有明显的约束作用.
分别研究在不同停止施工时间时,基坑护坡桩水平变形趋势,计算停止施工时间为30 d、90 d、180 d以及365 d时护坡桩水平位移变形情况,统计最大变形位置处结果,见表7、图8:
由表7、8可知,从停止施工时间和护坡桩变形之间的关系可以看出,随着停止施工时间的增加,护坡桩水平变形逐渐增大,变形速率在不断减小,在前1个月内,护坡桩变形增量和变形速率都是最大的,变形量占总变形60%,180~365 d这段时间变形增量以及变形速率逐渐减小,当停止施工365 d时,变形速率为0.014 mm/d.这是由于在基坑停止施工前期时,护坡桩桩后粉细砂土体处于初始蠕变阶段,发生较大弹性蠕变变形,使得护坡桩位移增大并以较快的速度增长,随后粉细砂土蠕变速度逐渐降低.即护坡桩水平变形分为3个阶段,阶段一是快速初始变形,阶段二是稳定变形,阶段三是加速破坏变形,通过对表8的分析可知,护坡桩的主要变形发生在阶段一,该阶段持续时间较短,在1个月之内.稳定变形阶段持续时间较长,该阶段变形速率逐渐趋于0,变形量不断增加,当桩后土体变形过大导致护坡桩变形急剧增加时,护坡桩变形进入加速破坏变形阶段.
图 12为基坑长边方向剖面以及基坑整体土体竖向位移云图,其中“-”表示向下沉降,“+”表示向上隆起.在基坑长期暴露下,桩后土体由于蠕变效应其竖向沉降变形明显增加,从开挖完毕停止施工,5 a时间内,桩后地表沉降最大值从19.9 mm增加到42.5 mm,最大沉降变形位置在距基坑边13 m左右.
图 13、14分别为不同暴露时间下基坑长边与短边方向地表竖向沉降位移变化曲线.当基坑开挖至坑底瞬时,桩后地表沉降变化明显,最大值为12.88 mm,位于距基坑边13 m附近.1个月后该位置由于粉细砂土蠕变效应沉降达到23.64 mm,蠕变作用引起的变形占总变形的45.5%.3 a后该位置相比于1月蠕变增量达到5.86 mm,占总变形的19.9%.
图 12 不同时间基坑土体竖向位移云图(单位:m)
Fig.12 Cloud diagram of vertical displacement of foundation pit soil at different times
图 13 基坑长边方向地表竖向位移变化曲线
Fig.13 Curves of vertical surface displacement along the long side of foundation pit
图 14 基坑短边方向地表竖向位移变化曲线
Fig.14 Curves of vertical surface displacement along the short side of foundation pit
由地表竖向沉降位移变化曲线可以看出,曲线呈现凹槽型变化规律.随着时间的发展,无论是长边方向还是短边方向,地表沉降位移变化曲线趋势是大致相同的,基坑长期暴露状态下并未改变地表沉降变形最大值的位置.在基坑停止施工期间,地表竖向沉降还在继续增加,表现出时间效应.
通过对图 15、16分析可知,距坑边13 m左右位置的特征点7的沉降位移较大,其竖向蠕变速率减小较慢.特征点7附近位置为桩后地表沉降最大位置点,该点从基坑开挖结束至暴露1a内蠕变增量达到15.35 mm.远离坑边位置的特征点9、10号点的沉降位移最小,1a内蠕变增量分别为5.56 mm与4.36 mm,其竖向蠕变速率减小较快,该两点蠕变速率在1个月后逐渐趋于稳定.
图 15 各特征点竖向蠕变变形随时间变化曲线
Fig.15 Curve of vertical creep deformation at each characteristic point with time
基坑桩后土体各特征点的位置不同,其蠕变量、蠕变速率也不同,但各特征点竖向蠕变稳定时间相差不大.7号点前3个月内的平均竖向蠕变速率为0.14 mm/d,1 a内的平均水平蠕变速率为0.04 mm/d.特征点9、10前三个月的平均竖向蠕变速率为0.035mm/d与0.024 mm/d,1 a内的平均竖向蠕变速率为0.015 mm/d与0.012 mm/d,即最远离坑边位置处土体竖向沉降蠕变量以及蠕变速率最小.如以0.1 mm/d作为蠕变稳定标准,5个特征点在1 a内基本达到稳定.当基坑开挖支护完毕,随着暴露时间的增加,地表沉降变形在不断增大,但其平均蠕变速率在逐渐下降.
将数值模拟计算结果与沉降监测点6、7的实测数据进行对比.图 17的沉降时程曲线表明,基坑外地表沉降的有限元计算结果与实测数据变形趋势相同,规律一致,说明此蠕变模型可以较准确反映基坑长期暴露时的蠕变变形规律.
护坡桩桩身的水平位移能够较好地体现基坑的变形程度,图 18给出护坡桩桩身的水平变形的监测结果,图中4个监测点是在停工时期对护坡桩水平位移增量的监测结果,监测时长为80 d(即从基坑停止施工第160天起开始监测).
根据基坑护坡桩水平位移观测点的实测观测结果来看:在停工前期,由于基坑后续加固支护还未完成,基坑整体不够稳定.粉细砂土的蠕变变形表现明显,导致护坡桩水平位移随时间的推移有增长的趋势.随着时间的不断推移,水平位移增量有所缓和,后期变形增量有所减小.因此,在停止施工中要充分考虑时间效应,加强对基坑蠕变变形的观测.
图 19给出基坑长边方向,某一护坡桩桩身不同位置的水平变形时程曲线的计算值与监测值的对比,监测工作是从停止施工第160天起进行的水平位移增量测量,从图中可以看出,护坡桩桩身不同位置的水平位移计算结果在变形大小和趋势上都与实测结果都有一定的吻合性以及相似的规律,证明了在参数反演过程中,最终确定参数的准确性.
因此,通过参数反演利用实测数据调整蠕变参数,生成蠕变模型对超期使用下基坑蠕变变形预测是可行的.ABAQUS软件中采用的时间硬化蠕变模型可以较好地对基坑未来稳定性进行合理预测,其预测结果为超期服役基坑工程进度安排及后期管理提供依据.
本文利用时间硬化蠕变模型反映粉细砂土超期服役下的蠕变效应,通过室内三轴不排水蠕变试验结果拟合蠕变参数A、m、n,利用ABAQUS软件建立粉细砂基坑三维数值计算模型,模拟实际粉细砂深基坑工程超期使用下护坡桩侧向蠕变变形范围及趋势,对基坑未来稳定性进行合理预测.得到以下主要结论:
(1)粉细砂土由于蠕变效应引起基坑土体水平变形随时间不断发展,最大变形位置在开挖面附近.其水平蠕变速率不断减小,但变形会持续发展,累计变形量较大.桩后不同位置点土体水平蠕变变形速率基本在两个月左右时间趋于平稳;
(2)基坑在停止施工长期暴露的情况下,坑外地表会发生沉降,随着时间的推移沉降变形会不断发展.其竖向蠕变速率前期较大,后期不断减小.最大沉降变形位置在距坑边13 m左右位置.土体竖向蠕变量随着距坑边距离的增大呈现先增大后减小的分布规律;
(3)监测数据与数值模拟计算结果均说明粉细砂土具有蠕变特性,因此深基坑在超期服役下会表现出时间效应,超期服役状态下基坑变形不可忽视;
(4)时间硬化蠕变模型合理地模拟了某市三馆项目粉细砂土基坑开挖支护以及超期服役的变形规律.利用监测数据通过参数反演,修正的蠕变参数使计算结果更加贴近实际情况.成功地预测了基坑未来稳定性,为超期服役基坑工程进度安排及后期管理提供依据.