基金项目:中国高校产学研创新基金(2021DZ023); 潍坊市科学技术发展计划(2021GX005)
第一作者:李志强(1972—)男,副教授,主要从事隧道工程、路基工程方面的研究,E-mail:wfulzq@163.com 通信作者:刘路路(1990—),男,博士后,助理研究员,主要从事路基工程方面的研究,E-mail:believeliululu@163.com
(1.潍坊学院 建筑工程学院, 山东 潍坊 261061; 2.东南大学 岩土工程研究所,江苏 南京 211189; 3.长安大学 特殊地区公路工程教育部重点实验室,陕西 西安 710064)
(1.School of Civil Engineering and Architecture, Weifang University, Shandong Weifang 261061, China; 2.Institute of Geotechnical Engineering, Southeast University, Nanjing 211189, China; 3.Key Laboratory of Special Area Highway Engineering, Ministry of Education, Chang'an University, Xi'an 710064, China)
Tunnel in cold region; Similarity relation; Temperature field; Model test
DOI: 10.15986/j.1006-7930.2023.01.009
许多寒冷地区隧道出现在加拿大、挪威、中国、俄罗斯和日本[1-3].在中国西北和东北地区,在通风条件下,寒冷地区隧道衬砌与空气之间发生强烈的热传递,导致结构开裂、漏水、冰覆盖和冰堵塞排水沟[4-5],甚至,一些隧道每年最多不能使用8~9个月,这对交通产生了负面影响.温度场对分析围岩冻结膨胀具有重要意义,是保温层计算的重要参考.因此,保温层设计成为解决寒冷地区隧道抗冻问题的一个紧迫重要问题[6-8].
为了研究运营寒区隧道衬砌、围岩温度场变化规律及保温层保温效果,需要在隧道衬砌及内部围岩埋设一定数量测试传感器,但是考虑到运营隧道防排水体系、混凝土结构体系、通风照明体系等已完成[1, 3],传感器的埋设往往存在较大困难,目前,针对通风条件下寒区隧道温度场建立的数学模型计算参数的选取上,未能建立起一个具有参考价值的标准,尤其是数值模型参数的选取主要局限在前人研究成果[9-11, 13],并且不少学者采用有限元模拟得到的结果差异性较大[6, 7, 12, 14].缩尺物理模型试验可以研究不同工况条件下隧道温度场分布变化特征,并且可以为寒区运营隧道的数值模拟提供计算参数.
大阪山隧道长度1 530 m,采用纵向变率模型(3 m)模拟隧道全长[15],按照断面相似比1/37进行缩放,将围岩及衬砌相似材料搭建成一个模型小山,借助多排冷冻管将模拟的大气低温传递给围岩及隧道洞口,以便达到模拟隧道温度场的目的
模型试验采用的冷冻仪器为安徽理工大学大学煤矿深井建设技术国家工程实验室XT5710冻土模型试验冷冻系统,冷冻系统分为主机动力系统与外循环系统,制冷剂采用95%工业酒精,温度可调范围为-40~60 ℃.
模型试验设计如果满足相似第三定理规定的全部相似条件往往是比较困难的,所以一般采用近似相似方法,使得主要相似条件得到满足,从而获得工程需要的近似相似条件.本文主要研究通风条件下的传热模型,主要考虑热学相关参数,而对于力学相关参数关系不大.
寒区隧道围岩传热微分方程为
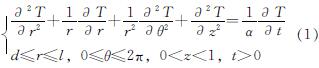
式中:T为隧道围岩温度,℃; α为岩石的热扩散系数,m2/s; r为围岩径向深度,m; l为温度场影响半径,m; z为围岩冻结深度,m
洞壁围岩与洞内气体发生对流换热,影响范围以外的围岩温度以及围岩初始温度设为等于原始地温,将多心圆隧道断面简化为圆形,并且采用极坐标形式表示传热方程,即

在冻结锋面上有
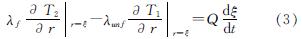
初始条件与边界条件为
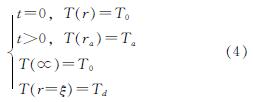
式中:T0为冻土和未冻土中r处的温度,℃,下标n=1为未冻土,n=2为已冻土; t为时间,d; αn为热扩散系数,m2/d; r为柱坐标,m; λunf为未冻土的导热系数,kJ/(m·d·℃); λf为冻土的导热系数,kJ/(m·d·℃); ξ为冻结壁边界位置坐标,m; Q单位土体冻结时放出的潜热量,kJ/m3; Tn为隧道内空气温度,℃; Td为冻结温度,℃.
为了分析参数的影响,设与之相似的试验模型数学表达式为
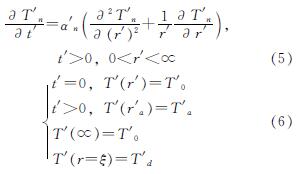
经过相似转换,可得到相似准则为
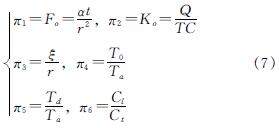
式中:π1~π7为相似准则; F0为傅里叶准则; K0为科索维奇准(C=α/λ); π3~π5均是温度准则,统一用θ表示; π6为几何准则,用R表示,整理后准则方程为
F(Fo·Ko·R·θ)=0(8)
为浇筑方便,本次隧道模型定为单心圆隧道,考虑到冷冻实验室的占地面积、隧道模型加工性及经济性、隧道模型试验中可操作性等因素,最终确定隧道断面几何比为1:37,大阪山隧道全长1 530 m,按照几何比1:37,得到模型长度41 m,这个长度远远超出了冷冻系统尺寸,是不可取的.
对于隧道细长比较大结构,若对整体进行缩尺模型试验,则需要采用变率模型,其中,变率参数的选取对模型试验结果的可信度及修正性起着重要作用,参考长安大学谢永利课题组[12-14]港珠澳海底隧道通风模型试验,根据隧道通风物理试验的经验,可取长度方向变率k=4,则隧道模型长度为10.25 m.
由于室内试验条件限制,10.25 m的长度仍然存在操作困难.根据尼古拉兹试验结果[15-16],黏性流体本身具有自模性,当雷诺系数Re增加到某个程度,原型隧道雷诺数Re处于自模区[16]以内,沿着程阻力相似不一定使得雷诺系数相等,称之为“自模化状态”,在此区域中,由于沿程阻力系数不受雷诺数影响,因此,只要是原型与模型同处于同一自模区就能自动保证流动相似.几何相似的封闭系统中不可压缩流体,只需两个系统雷诺数相同就能满足所有相似条件.黏性流体流动时,只有确保所研究的区域进入自模区,才可保证研究的正确性.
原型雷诺数为
Re=(ρvD)/u=(1.225×3.0×9.15)/(1.66×10-5)=1.35×106(9)
原型沿程阻力系数为0.025.
式中:ρ表示空气密度,取值1.225 kg/m3; v表示风速,取洞内外自然风压在洞内产生的风速,取值3 m/s; D表示隧道直径,m; u表示空气黏质系数,取值1.66×10-5 m2/s.
模型隧道表面粗糙度K的测量采用内径千分尺测量,在隧道进口与出口分别选取10个测点,进行测量,计算得出K=0.000 324.
模型雷诺数为
Re=(ρvD)/u=(1.225×4.8×0.4)/(1.66×10-5)=1.417×105(10)
模型相对粗糙为
K/D=(0.000 324)/(0.4)=0.000 81
由莫迪图可知,模型进入自模区.
所以模型与原型在隧道断面流动上是保持相似的[12],考虑冷冻设备尺寸问题,模型隧道长度定为3 m,由《大阪山病害处治施工图设计》可知,进洞段地址条件较差,进口段为Ⅱ类围岩且储水较大,对于Ⅱ类围岩,C25初支混凝土≥40 cm,路面变形缝沉降围岩为绢云母绿泥石钙质片石,主洞二次衬砌为68 cm后模筑C25混凝土,隧道原型与模型主要设计参数如表1.图1为隧道模具,图2为养护成型隧道模型.
根据科索维奇准则Ko=(Qp)/(TpCp)=(Qm)/(TmCm),可得

因为模型与原型衬砌材料都采用C25混凝土,材料相同,故CC=1,CQ=1,得CT=1即Tp=Tm.所以模型中衬砌混凝土各点的温度与原型中对应几何相似点的温度值相等.模型围岩材料内部温度分布值要结合围岩材料的测试导热系数,具体计算过程参考2.3围岩材料配置.
大阪山隧道的衬砌为C25混凝土,由《大阪山病害处治施工图设计》可知,C25初支混凝土≥40 cm,主洞二次衬砌为68 cm后模筑C25混凝土,经过几何缩尺之后,初衬厚度为1.84 cm,二衬厚度为1.08 cm.由于混凝土中粗骨料效应,模型试验中无法采用常规的混凝土进行浇筑,拟采用C25细粒混凝土进行代替,细粒混凝土的选取主要参考其导热系数与C25混凝土的接近程度.
对于细粒混凝土的配置,主要考虑到衬砌之间需固定5 mm保温层,保温层与模板之间距离缩短为17.5 mm,根据粗骨料不能超过浇筑厚度的1/2的原则,采用8 mm方孔筛对粗骨料进行筛分,然后冲洗,晾晒.并且要保证所选用石子在水中浸泡不少于24 h直到含水量基本没有变化,所有冲洗并晾晒石子中的含水量对配比没有太大影响.
细粒混凝土的配合比:
水:水泥:砂子:石子=0.38:1:1.11:2.72
试验相关材料参数见表2.
经查阅资料,标准C25混凝土导热系数为2.461 W/m·K,对模型衬砌混凝土的导热系数进行10组测试,取平均值2.410 W/m·K,与模型标准C25混凝土导热系数近似相等.
根据1/37几何缩比,若采用现场聚氨酯保温材料,则模型衬砌表面与内部保温材料厚度为1.35 mm,该厚度在模型试验操作性差,误差大,并且聚氨酯保温材料具有较高的脆性,与模型隧道的密贴程度较差,增加了接触热阻的影响,对试验结果的影响程度较大.所以考虑采用代替材料,通过查阅相关材料,并进行相应的试算,橡塑保温材料柔软度较高,导热系数小,裁剪方便.其铺设方式与现场隧道一致,衬砌表面1 cm橡塑保温层,衬砌内部0.5 cm橡塑保温层.
采用热阻法进行保温层厚度的相似计算,计算模型按照圆筒壁导热方式进行,在圆筒壁的稳态导热中,不同半径处的热流密度与半径成反比.但是,通过整个圆筒壁面的热流量为常量,不随半径而异,所以得到热流量方程为
Φ=2πrlq=(2πλl(t1-t2))/(ln(r1/r2))(12)
式中:Φ热流量,W; r1、r2为圆筒壁内外半径,m; t1、t2为圆筒壁内外壁面温度,℃; Φ为圆筒长度,m; Φ为导热系数,W/m·K.
根据热阻定义,得到整个圆筒壁的导热热阻为
R=(Δt)/Φ=(ln(r2/r1))/(2πλl)(13)
对衬砌表面保温材料而言:
设聚氨酯保温材料导热系数为λj,衬砌表面保温材料内半径为λj1,衬砌表面保温材料外半径为γ0,长度为l,则热阻Rj为
Rj=(ln(r0/rj1))/(2πλjl)(14)
式中:λj=0.018 W/m·K; γj1=12.2 cm; γ0=12.335 cm; l=300 cm.
设橡塑保温材料导热系数为γx,衬砌表面保温材料内半径为γx1,衬砌表面保温材料外半径同为γ0,长度同为l,则热阻Rx为
Rx=(ln(r0/rx1))/(2πλxl)(15)
式中,λj=0.034 W/m·K; γj1=12.2 cm; γ0=13.2 cm; l=300 cm.
经计算得
(Rx)/(Rj)=(0.133)/(0.033)=4.03(16)
在平壁导热中,与之对应的表达式为
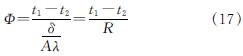
为了保证代替保温材料与按照几何缩比得到的1.35 mm聚氨酯保温层具有相同的保温效果,必须保证两者具有相同的热阻,从热阻效果来看,1 cm橡塑保温层1.35 mm聚氨酯保温层的保温效果高出4.03倍.
根据能量守恒定理,在外界热量不发生损失的情况下,通过两种保温材料下的热流量相等,最终得到1.35 mm聚氨酯(原型几何缩比后的模型厚度)保温层背后的温度分布,可得
tj1=tj2+(tx1-tx2)/(Rx)Rj(18)
式中:tj1为聚氨酯保温层表面温度,℃; tj2为聚氨酯保温层背后温度,℃; Rj为聚氨酯保温材料热阻,m2·K/W; tx1为橡塑保温层表面温度,℃; tx2为橡塑保温层背后温度,℃; Rx为橡塑保温材料热阻,m2·K/W.
对衬砌内部保温层而言:
Rj=(ln(r0/rj1))/(2πλjl)(19)
式中:λj=0.018 W/m·K; γj1=14.04 cm; γ0=14.175 cm; l=300 cm.
Rx=(ln(r0/rx1))/(2πλxl)(20)
式中:λj=0.034 W/m·K; γj1=14.04 cm; γ0=14.54 cm; l=300 cm.
经计算得
(Rx)/(Rj)=(0.055)/(0.028)=1.96(21)
在平壁导热中,与之对应的表达式为
Φ=(t1-t2)/(δ/(Aλ))=(t1-t2)/R(22)
从热阻效果来看,得出0.5 cm橡塑保温层比1.35 mm聚氨酯保温层的保温效果高出1.96倍.
同衬砌表面保温层计算方法相同,最终可获得按照几何缩比得到的1.35 mm聚氨酯保温层背后的温度分布.
由《大阪山病害处治施工图设计》可知,大阪山隧道一带广泛分布片岩类、灰岩类、大理岩类等地层,固定某一类岩石的导热系数存在较大误差,所以采用主要岩石导热系数的平均值作为现场隧道围岩的导热系数,取值为2.641 W/m·K.
拟采用配置材料来代替围岩材料,要求配置围岩材料导热系数尽可能接近现场围岩.如图3所示
围岩材料配合比:
水:砂子:石灰:石子:黏土=0.35:1.5:0.2:0.6:2.0.
相关材料参数见表2.
根据科索维奇准则Ko=(Qp)/(TpCp)=(Qm)/(TmCm),可得

因为模型与原型围岩材料不同,原型围岩导热系数为2.523 W/m·K,热扩散系数为0.114 m2/d,模型围岩导热系数为1.551 W/m·K,热扩散系数为0.034 m2/d,得
CC=(Cp)/(Cm)=(αp/λp)/(αm/λm)=(23.17)/(45.62)=0.51(24)
CC=0.51,CQ=1,得CT=1.96即Tp=1.96Tm.所以模型中围岩材料各点的温度分布与原型中对应几何相似点的温度值为1.96倍关系.
将模型试验得到的温度数据进行如下处理:将纵向温度数据采用归一化法及径向温度数据按照几何比还原到现场隧道,与现场实测数据对比分析.
大阪山隧道出口风速大于进口风速,且出口温度低于进口温度,与模型的温度分布类似,为了方便与模型试验数据对比分析,作图中将大阪山出口位置记作0 m,进口位置记作1 30 m.大阪山11月、12月洞口温度和试验空气温度在-8.4 ℃、-10.6 ℃下与模型隧道洞口温度接近.经现场实测,大阪山隧道11月、12月洞口风速2.0~3.0 m/s,取模型试验通风风速2.6 m/s下试验数据,故对这两组数据进行对比分析.
由图4~5可以看出:模型与现场洞内气温变化曲线都呈二次抛物线型规律,对现场与模型温度数据分别拟合得到方程为
T=al2+bl+c(25)
式中:T为温度,℃; l为隧道进深,m; a、b、c为方程系数.表3为大阪山11月、12月下方程系数a、b、c的取值.
现场隧道洞口温度变化温差较大,洞内温度变化幅度较小,虽然洞口模型数据与现场数据接近,但是洞内气温明显高于现场,存在一定误差,所以采用修正系数对隧道模型洞内气温方程进行修正,修正方程为
T=[mal2+bl+c]-n(26)
式中:11月份模型方程修正系数m、n分别为-4.78×10-6、2.51; 12月份模型方程修正系数m、n分别为-5.96×10-6、4.12.
将修正好的模型数据与现场数据进行Pearson相关性分析,如图6~7所示,11月、12月现场数据与修正模型数据相关系数r分别达到0.987、0.808,属于高度相关,说明在一定程度上可以通过试验空气温度-8.4 ℃、-10.6 ℃下隧道模型洞内气温来预测现场隧道洞内气温分布.
虽然开展低温气流对模型山体进行降温试验,但效果还是低于实际工况下的大气环境,毕竟模型山体会与周围环境进行热交换,导致实际降温效果远远低于实际环境,这就导致模型洞内温度和现场温度存在差别.
将按照断面几何相似比反推的模型围岩冻结深度与吴紫汪等[17]现场测试的大阪山11月、12月围岩冻结深度进行对比分析.为了方便与模型试验数据对比分析,作图分析时将大阪山出口位置记为0 m,进口位置记为1 530 m.
由图8~9可以看出,大阪山隧道11月洞内650~1 500 m范围内未出现冻结区域,模型隧道550~1 170 m范围内未出现冻结区域; 大阪山隧道12月全长出现冻结区域,而模型隧道洞中仍存在约250 m的未冻结区域.
提取图8~9冻结深度数据,进行非线性回归分析[18],可以看出,进、出口围岩冻结深度随着隧道进深增加成二次抛物线型衰减,回归方程见图8~9.通过相似比反推的模型隧道冻结区深度明显低于现场隧道,但是,冻结深度的变化规律与模型隧道相似,现场数据与反推模型数据存在近似的倍数关系,所以,我们采用修正系数对模型隧道冻结深度进行处理,两种工况模型的修正系数分别为1.35、1.2,模型修正数据见表4~5.
对修正好的模型数据进行Pearson相关性分析[19-20],11月、12月现场数据与修正模型数据相关系数r分别为0.955、0.993,属于高度相关,说明在一定程度上我们可以通过试验空气温度-8.4 ℃、-10.6下模型隧道围岩冻结深度来预测现场隧道11月、12月围岩的冻结深度.
表4 大阪山隧道11月及修正模型边墙围岩冻结深度
Tab.4 Freezing depth of surrounding rock of side wall of Osaka mountain tunnel in November and revised model
(1)基于相似理论,推导出寒区运营隧道温度场模型试验相似指标,得出模型的几何、温度等相似比,配置一定的相似材料,建立了寒区运营隧道模型试验平台验.
(2)采用纵向归一化及径向几何比还原法,结合现场实测数据,从隧道洞内气温,围岩冻结深度方面与模型试验数据进行了对比分析,修正的模型试验结果与现场实测数据比较符合,说明本次相似关系的拟定是合理的.研究结果能够为从事寒区运营隧道方面的模型试验研究提供指导,并且可以为数值计算参数的选取提供一定的参考依据.