基金项目:国家自然科学基金项目(51968058),内蒙古科技大学建筑科学研究所开放基金项目(JYSJJ-2021M01)
第一作者:高春彦(1978—),女,博士,副教授,主要从事组合结构及结构抗震性能研究. E-mail:gao-197844@163.com 通信作者:樊 荣(1997—),女,硕士,主要从事组合结构性能研究.E-mail:1461523125@qq.com
(1.内蒙古科技大学 土木工程学院,内蒙古 包头 014010; 2.中钢设备有限公司包头分公司,内蒙古 包头 014010; 3.上海宝冶集团有限公司,上海 201900,4.包钢西北创业建设有限公司,内蒙古 包头 014010)
(1.School of Civil Engineering, Inner Mongolia University of Science and Technology, Inner Mongolia Baotou 014010, China; 2.Sinosteel Equipment & Engineering Co., Ltd. Baotou Branch, Inner Mongolia Baotou 014010, China; 3.Shanghai Baoye Group Co., Ltd., Shanghai 201900, China; 4.Baogang Northwest Venture Construction Co., Ltd., Inner Mongolia Baotou 014010,China)
compact reinforced composite(CRC); steel fiber volume content; confinement coefficient; bearing capacity
DOI: 10.15986/j.1006-7930.2023.01.011
CRC(全称Compact Reinforced Composite),即密实增强混凝土,属于超高性能混凝土的一种.其优点是具有超高抗压强度、高弹模、高韧性和优良的抗震、抗冲击性能以及耐久性等,由此,CRC目前广泛应用于土木工程、军事领域、海上工程等领域[1-9].
CRC是由水泥基体材料加上大掺量细短钢纤维组成,与目前研究和应用广泛的RPC(Reactive Power Concrete)的区别是钢纤维掺量通常在3%~6%之间,纤维长度为6 mm左右,直径≤0.2 mm.而后者是由中等长度钢纤维与基体组成,钢纤维长度一般为13 mm,体积掺量不大于2%.目前国内仅梁兴文教授的团队对CRC材料的基本力学性能、CRC混凝土梁的受弯及受剪性能进行了研究,取得了一定的研究成果[10-14].由于CRC与高强混凝土相似,在高应力下会呈现爆裂式脆性破坏,延性较差.若将CRC填充至钢管形成钢管CRC柱,可以大大增强核心CRC的延性,这就使得这种构件用于超高层建筑的底部或重要建筑物的关键部位成为可能.目前,国内外学者对钢管CRC柱的研究鲜见于报端,但Wang[15]、Portolés[16]、颜燕祥[17]、王杨[18]、戎芹[19]、罗华等[20]等对钢管RPC柱的破坏机理、承载能力、应力-应变全曲线方程以及影响构件力学性能的控制指标和参数等取得了一些重要的研究结论,为钢管约束CRC轴压力学性能的研究奠定了理论和试验基础.
本文拟对18根方钢管约束CRC棱柱体试件进行轴压试验,分析变化参数(钢纤维体积掺量、套箍系数)对轴压短柱的破坏形态、承载力以及变形的影响,同时制作了6根非约束CRC对比试件,研究方钢管约束CRC试件的荷载-变形关系以及钢管横向变形系数的发展规律,以期为研究钢管约束 CRC的轴压力学性能提供参考.
采用42.5R普通硅酸盐水泥; 硅灰中SiO2含量为94%; 采用白色石英砂,粒径分别为:10~20目、20~40 目、40~70 目、70~120 目、325目; 钢纤维采用镀铜微丝钢纤维,直径0.205 mm,长度6.7 mm,抗拉强度为2 876 MPa,长径比为33; 采用聚羧酸系减水剂.CRC立方体试块边长为100 mm,棱柱体试件尺寸为100 mm×100 mm×300 mm; 不同钢纤维体积掺量的核心CRC采用了不同的配合比,CRC的配合比以及基本力学性能见表1.
钢管边长为100 mm,分别由壁厚为10 mm、 12 mm、14 mm、高度为300 mm的钢板拼焊而成.钢材物理力学特性见表2.
共设计制作3组6根非约束CRC试件和9组18根方钢管约束CRC试件,变化参数为套箍系数(直接变化参数为钢管壁厚,分别为10 mm,12 mm,14 mm)和钢纤维体积掺量(4%,5%,6%).所有试件边长均为100 mm,高度均为300 mm.非约束试件的命名方法以CRC-4-1为例,CRC表示Compact Reinforced Composite(密实增强混凝土),4表示钢纤维体积掺量为4%,1表示同组第一个试件.方钢管约束试件以CCRC-4-10-1为例,CCRC表示Confined Compact Reinforced Composite,10表示方钢管壁厚,其余两个数字的含义与非约束试件相同.
基于试验目的,即钢管仅对核心CRC提供侧向约束作用,因此,浇筑CRC前在钢管内壁涂上润滑剂,CRC浇筑完毕后,用保鲜膜将试件密封,静置24 h,然后放入标准养护室进行养护.待试件养护成型后,磨平试件上端,将盖板放于试件上端进行焊封,试件制作完成.
非约束CRC试件的破坏过程基本相同.加载初期试件外形并无明显变化,随着荷载的增加,伴随着少量混凝土碎渣掉落,试件表面出现若干细微裂缝; 当荷载增加至某一值时,试件突然碎裂,同时发出“嘭”的巨大声响,出现一条或者多条斜向裂缝贯穿试件表面,试件典型破坏形态如图2所示,为沿斜截面的剪切滑移破坏.
不同参数方钢管约束CRC试件的破坏过程也基本相同,由于核心CRC的高弹模特性,在达到峰值荷载的85%之前,试件外形没有明显变化,在此阶段荷载-变形关系呈直线变化,试件处于弹性受力阶段.当超过峰值荷载后,绝大多数试件基本在中部以上钢管焊缝被撕裂,在焊缝撕裂范围内核心CRC被压碎.这是由于轴向压力仅施加在钢管内的CRC上,CRC在纵向受压的同时,横向膨胀并挤压钢管,而由于钢管的焊接质量问题,最终导致出现不同程度的焊缝撕裂破坏.图3(a)、(b)、(c)为9组方钢管约束CRC试件的破坏形态.图3(d)给出试件CCRC-4-12在钢管剥离后核心CRC的破坏形态.可以发现,核心CRC的破坏主要发生在钢管焊缝撕裂范围内,除了不规则的压碎开裂,主裂缝仍为沿斜截面的剪切滑移裂缝.说明尽管核心CRC受到钢管的约束,间接提高了其抗剪强度,但抗剪强度仍远远低于约束CRC的抗压强度,故发生沿斜截面的剪切滑移破坏.
由试验过程可知,随着钢纤维掺量和套箍系数的增加,试件的破坏形态没有明显变化.
图4所示为试件的荷载-纵向变形曲线,图5所示为试件的荷载-钢管横向变形系数U(εh/εv)曲线.图5中实心圆点表示钢管屈服时的位置.由于本文试验试件的套箍系数ξ均较大,各试件在加载时不存在明显的峰值荷载点,当变形Δ>5 mm 之后,试件的荷载会趋于稳定.鉴于此,取轴向荷载—纵向变形曲线Δ=4~5 mm左右对应的荷载作为方钢管约束CRC的受压极限荷载[10].
由图4可知,试件的轴向荷载—纵向变形曲线基在峰值荷载的85%之前呈线性变化.在该阶段钢管泊松比在0.49~0.64之间(图5),呈现出近乎垂直的直线,且钢管泊松比大于钢管单轴受力时的泊松比,说明从加载开始方钢管就对其内部CRC产生了约束作用.钢管屈服后,试件由弹性阶段进入弹塑性阶段,此时随荷载的增加U值增长的速度加快(图5).
加载至峰值荷载后,核心CRC内部微裂缝逐渐发展,但由于试件套箍系数较大,在钢管约束下变形增大的同时荷载没有下降,此时轴向荷载基本不增加而钢管的横向变形系数U持续增加,当U>1时,钢管中以环向拉应力为主,对核心CRC的约束更大.
表3给出所有试件的主要特征点参数.其中,ξ为套箍系数,ξ=fyAs/fcAc,式中:fy、fc分别为钢管屈服强度和无约束CRC的抗压强度; As、Ac分别为钢管和核心CRC的截面面积; εp为无约束CRC的峰值应变; Pu为试件的轴压极限荷载; σ0、ε0分别为方钢管约束CRC试件的峰值应力及对应的峰值应变.
由表3可知,钢纤维体积掺量为4%时,套箍系数增加时,σ0分别提高了17%和45%,ε0分别提高了15%和26%; 钢纤维体积掺量为5%时,σ0分别提高了15%和34%,ε0分别提高了18%和31%; 钢纤维体积掺量为6%时,σ0分别提高了15%和40%,ε0分别提高了19%和26%.钢管厚度为10 mm时,钢纤维体积掺量增加时,σ0分别提高了9%和10%,ε0分别提高了4%和3%; 钢管厚度为12 mm时,σ0分别提高了7%和8%,ε0均提高了6%; 钢管厚度为14 mm时,σ0分别提高了1%和6%,ε0分别提高了8%和3%.钢纤维体积掺量为4%,5%和6%的约束CRC的σ0较非约束CRC平均增大了1.44倍,ε0增大了2.1倍.由此可知,CRC在方钢管约束下,脆性得到了改善,试件的承载能力和变形能力显著提高.钢纤维体积掺量和套箍系数的增大都会使方钢管约束CRC的峰值应力和峰值应变有一定程度的提高,其中套箍系数对方钢管约束CRC的影响最显著.
基于韩林海提出的本构模型[21],综合上述试件的特征点参数,得到方钢管约束CRC轴向应力-应变关系表达式,即
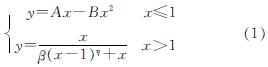
式中:y=σ/σ0、x=ε/ε0.结合试验数据,拟合得到的A、B、β、η值见表4.
由表中数据发现,A、B是近似等于2.016和1.135的曲线上升段修正系数,如图6所示.
β、η是与试件套箍系数ξ相关的曲线下降段修正系数.β与ξ间的关系如图7所示.
通过拟合得到β与ξ之间的关系式:
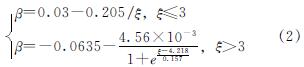
采用同样的方法得到η与ξ间的关系如图8所示.通过拟合得到η与套箍系数ξ的关系式为
η=1.128+0.186/ξ(3)
方钢管约束CRC本构模型计算曲线与试验曲线对比结果如图13所示.由图可以看出,模型计算曲线与试验曲线吻合较好,可以有效反映在钢纤维体积掺量为4%~6%,套箍系数为2.5~4.2范围内,方钢管约束CRC的应力-应变曲线的特征及规律.
(1)方钢管约束CRC棱柱体短柱的典型破坏形态为钢管焊缝撕裂破坏,焊缝撕裂范围内核心CRC被压碎; 钢管剥离后核心CRC的破坏形态为沿斜截面剪切滑移破坏;
(2)由于试验试件的套箍系数较大,方钢管约束CRC轴压短柱的荷载—变形曲线没有明显的下降段,在峰值荷载的85%以前,试件基本处于弹性阶段,钢管屈服后横向变形系数U随荷载的增加逐渐呈水平向发展,钢管对核心CRC的约束不断增强;
(3)套箍系数的变化对试件轴压力学性能的影响最为显著,使核心CRC轴压强度最大提高了45%,纵向变形最大提高了31%.相比较而言,钢纤维体积掺量对核心CRC的轴压强度和纵向变形影响较小,分别最大提高了10%和8%;
(4)建立了方钢管约束CRC轴心受压应力—应变本构关系模型,计算结果与试验结果吻合较好.