基金项目:国家自然科学基金资助项目(51578225)
第一作者:吴 曦(1987—),男,博士,讲师,主要从事结构工程抗震方面的研究.E-mail: wuxi_ce@163.com 通信作者:汪梦甫(1965—),男,博士,教授,主要从事结构工程抗震方面的研究.E-mail: wangmengfu@126.com
(1.湖南城市学院 土木工程学院,湖南 益阳 413000; 2.湖南大学 土木工程学院,湖南 长沙 410082)
(1.College of Civil Engineering, Hunan City University, Hunan Yiyang 413000, China; 2.College of Civil Engineering, Hunan University, Changsha 410082, China)
DOI: 10.15986/j.1006-7930.2023.01.015
收缩和徐变是混凝土的固有特性,两者引起的微观层次变形会导致混凝土截面开裂、水平构件挠度过大、预应力结构应力松弛、结构内力重分布等现象[1],这些都有可能影响混凝土结构正常使用.考虑混凝土的收缩徐变效应,并准确计算其变形是高层建筑、大跨度桥梁和大体积混凝土工程等混凝土结构设计和施工中必须解决的问题.预制叠合剪力墙是一种半预制结构体系,最近几年已作为主要承重结构构件在我国大量高层住宅项目中得到应用.该竖向承重结构体系由预制工厂制作的预制墙身和现场浇筑的夹心层部分组成,各叠合层混凝土龄期、配筋情况、环境温湿度条件差异,都可能影响混凝土收缩徐变反应.目前,众多学者和工程技术人员围绕预制叠合剪力墙的宏观受力性能展开了大量试验和理论研究,研究内容主要集中于结构抗震性能提高、结构计算分析、施工方法改进等方面[2-6],但针对微观层次的收缩徐变效应缺乏认识.
通常,混凝土构件主要由受拉性能良好的钢筋和抗压特性较好的混凝土组成,但两者在弹性模量、变形特性上存在差异,钢筋对混凝土收缩和徐变效应产生约束作用,在长期外荷载作用下混凝土结构构件内部存在内力协调效应.目前,混凝土收缩和徐变模型比较成熟的有ACI209、B3、GL2000、CEB-FIP2010等[7-10],这些多基于大量一维素混凝土试验构件观测数据统计得到,并不直接适用于配筋混凝土结构的长期收缩徐变效应预测.基于实际工程应用,一些研究人员通过试验测定钢筋混凝土结构的收缩徐变效应,并结合混凝土随时间变化效应对混凝土结构的长期收缩徐变效应进行了预测分析.其中,曹国辉等[11-12]通过对比试验发现配筋混凝土圆柱体徐变系数比素混凝土柱低,并比较了加载龄期对徐变效应的影响,提出了考虑配筋因素的徐变预测修正模型; 潘钻峰等[13]通过试验观察得到不同配筋情况下混凝土方柱收缩徐变情况,并建立了不同配筋率下收缩和徐变效应的理论计算公式,该公式可以用于预应力混凝土梁桥中截面应力计算; 丁敏等[14]在考虑钢材对构件截面内力重分布情况下,建立了钢管混凝土组合柱的长期徐变预测模型; Zou Dujian等[15]通过试验观测了普通剪力墙的收缩和徐变情况,并且基于B3模型,比较了框架-剪力墙结构中框架柱和剪力墙的变形差异; Huang Dunwen等[16]通过建立考虑混凝土时效性的混凝土收缩徐变增量计算微分方程,计算得到的型钢混凝土组合梁应力结果与试验结果吻合良好; Tu Bing等[17]基于AEMM法预测桥梁扩宽工程中新旧混凝土收缩徐变效应,并以此为基础建立有限元模型分析了T型梁桥的应力情况.
为研究预制叠合剪力墙在长期竖向荷载作用下的微观收缩徐变效应,本文设计制作一片小尺寸叠合剪力墙试件,对其施加竖向荷载,进行长期收缩徐变观测.结合试验得到的数据,建立考虑截面内力重分布的徐变预测模型,并通过参数分析研究混凝土强度等级、纵向钢筋配筋率、环境湿度、初始加载龄期和轴压比等参数变化对预制叠合剪力墙的收缩徐变效应的影响.
本次试验制作的预制叠合剪力墙试件尺寸为1 000 mm×1 450 mm×160 mm,墙体截面设置分别为预制层厚40 mm,夹心层厚80 mm.作为比较,本次试验设置了3个100 mm×100 mm×400 mm棱柱体试块同步进行素混凝土的收缩情况观测.试件的墙身水平向和竖向分布筋分别为Φ10@200和Φ10@150,暗柱纵向钢筋为4Φ12,暗柱箍筋为Φ6@150,剪力墙试件纵向钢筋配筋率为0.86%,配筋均满足《建筑抗震设计规范》GB50011—2010[18]三级抗震剪力墙构造要求,具体钢筋布置情况如图1所示.
试件制作按照预制叠合剪力墙的施工顺序进行:先制作钢筋骨架,其下端预留350 mm插筋,用于后锚入地基梁部分.先后分两次浇筑预制墙身,先浇筑第一面预制墙身,待第一面墙身混凝土强度达到75%设计强度,拆除模板,再浇筑另一面预制墙身,在达到75%设计强度后拆模,将预制墙身直立并锚固于混凝土基座上,浇筑夹心层和基座梁混凝土使得预制叠合剪力墙试件形成整体.
本次试验为文献[19]后续研究,试件所采用自密实混凝土配合比和工作性能参数与之相同.每批次混凝土留置立方体和棱柱体试块,与剪力墙试件放置在相同的正常实验室环境条件下养护,测得的自密实混凝土强度和弹性模量[20]如表1所示.通过钢筋拉拔试验测得试验所用钢筋强度和弹性模量[21]如表2所示.
收缩徐变是一个相对缓慢的长期变化过程,要求测试设备和试验环境具备较好的稳定性,本次试验采用振弦式应变计,其原理为通过应变计里的钢弦物理变化反应测点的应变变化.试件预制层采用表粘式振弦应变计,编号分别为A1~A11,在第二面预制墙身达到拆模强度后,通过嵌入混凝土内部的支架固定应变计.夹心层采用埋置式振弦应变计,编号为B1~B5,在制作钢筋骨架时将其固定于夹心层位置.作为比较的三个棱柱体安装表粘式振弦应变计,编号为C1~C3,在浇筑第二面预制墙身混凝土时同步留置.本次试验应变计布置如图2所示.
当试件夹心层混凝土达到28 d龄期,对试件施加竖向荷载开始徐变变形观测.按照图3所示,采用两个50 t螺旋千斤顶对试件施加竖向荷载,按照0.3轴压比(竖向荷载690 kN)施加竖向荷载.为保证顶部施加荷载均匀,试件顶部截面进行打磨处理,铺设金刚砂并设置散力钢板,试验过程通过力传感器对竖向荷载进行监控,并保证试验过程中其变化幅度不超过1%.为避免人为扰动和过大的环境条件变化,本次试验在湖南大学工程楼地下实验室进行.试验观测周期为12个月,试件加载初期的一个月时间内,观测频率为每天一次.第二个月观测频率调整为两天测量一次,最后十个月观测频率为每个星期测量一次.测量内容包括测点应变数据、力传感器竖向压力值、实验室温度和湿度.
通常,混凝土在外荷载作用下的变形主要分为因外力导致的瞬时弹性应变εe(t0)和徐变应变εc(t,t0)(如图4所示),长期徐变与瞬时弹性应变比值称为徐变系数φ(t,t0)(如式(1)所示)[10].但在开放环境条件下,混凝土在长期外荷载作用下会伴随收缩效应,混凝土的应变组成如图5所示.
φ(t,t0)=(εc(t,t0))/(εe(t0))(1)
图5 开放环境条件竖向荷载作用下混凝土应变组成
Fig.5 Strain composition of concrete under axial load in a normal environment
由图6可以看出,观测周期内,实验室内环境湿度相对稳定,相对湿度范围主要在80%~90%内波动.作为对比的三个棱柱体试件,收缩应变变化曲线发展趋势接近,应变随龄期的增长逐步增大,到后期增长趋于平缓,观测周期内最终收缩应变值为-126~-143 με.
图7为沿竖向荷载方向,预制层和夹心层各测试点的应变变化情况,所有测点应变随龄期不断增长,并随龄期的发展,应变增长速率放缓.夹心层各测点应变变化均比相应位置的预制层测点结果小.由表3可知,在竖向荷载作用下,预制层测点瞬时弹性应变值为-125~-146 με,夹心层测点B1、B4、B5为-119~-126 με,夹心层瞬时弹性应变接近预制层,表明预制层和夹心层接近完全粘结状态,整体协同工作性能良好; 夹心层收缩徐变增量范围为-188~-204 με,预制层应变增量范围为-202~-237 με,在相同应力状态下,预制层应变变化比夹心层大,这可能是因为与大气接触的预制层收缩变形更大所致; 夹心层和预制层测点应变比(应变增量与瞬时弹性应变比值)平均值分别为1.61和1.60,两者较为接近.
由图8可以看出,由于暴露于大气环境,水平方向预制层测点A2、A3应变曲线变化波动比较大,夹心层测点B2、B3应变曲线则相对稳定,但都呈现加载初期应变变化较快、后期应变变化曲线平缓趋势.根据表3,由于外力作用下竖直方向压缩,试件水平向瞬时弹性应变呈现拉伸状态,预制层测点A2、A3瞬时弹性应变为14 με和17 με,夹心层测点B2、B3瞬时弹性应变值为10 με和18 με,水平向瞬时弹性应变与竖直方向瞬时弹性应变比值约为0.12,略低于混凝土材料弹性泊松比[22]; 加载周期内,由初期的瞬时弹性受拉逐渐转变为收缩状态,水平方向收缩应变值随加载龄期增长不断增大,预制层与夹心层最终应变增量约为-140 με,与相同环境条件下棱柱体(C1、C2、C3)收缩应变变化值接近,这表明竖向荷载作用下预制层和夹心层混凝土横向应变变化以收缩作用占主导.单轴荷载作用下,垂直于荷载方向混凝土徐变效应较小.
剪力墙作为钢筋与混凝土共同受力的非均质结构,混凝土会随龄期增长产生收缩变形,相应地,与混凝土粘结良好的钢筋会因混凝土收缩协调变形,应力增大.长期收缩徐变效应下的剪力墙内部会产生变形协调与内力重分布.当预制叠合剪力墙满足以下假设:(1)忽略钢筋的松弛;(2)钢筋和混凝土有效粘结;(3)预制叠合剪力墙内部混凝土密实,各叠合层无滑移效应.恒定竖向荷载作用下剪力墙结构的截面受力特征如图9所示,可主要分为初期瞬时弹性和长期非线性阶段.
如图9(a)所示,在外力荷载加载初期,剪力墙符合平截面假定,混凝土与纵向钢筋协同作用,共同承担竖向荷载,根据平衡方程可知
εe(t0)=N/(Ec(t0)Ac+EsAs)=N/(Ec(t0)A0)·1/(1+nρ-ρ)(2)
混凝土和钢筋的弹性应力分别为
σc(t0)=Ec(t0)εe(t0)=N/(A0)·1/(1+nρ-ρ)(3)
σs(t0)=Esεe(t0)=N/(A0)·n/(1+nρ-ρ)(4)
式中:N为竖向荷载; A0、As和Ac分别为剪力墙截面面积、纵向钢筋面积和混凝土面积; t0为初始加载龄期; Ec(t0)和Es分别为混凝土和钢筋的弹性模量; ρ=As/A0为剪力墙竖向钢筋配筋率; n=Es/Ec(t0)为钢筋与混凝土弹性模量比.
图9 收缩徐变作用下剪力墙的变形协调
Fig.9 Deformation coordination of shear wall under the effect of shrinkage and creep
如图9(b)所示,长期荷载作用下,混凝土产生收缩和徐变效应导致混凝土应力松弛,钢筋应力增大,即剪力墙内部出现内力重分布,根据内力平衡关系
ΔσcAc+ΔσsAs=0(5)
同时,在满足钢筋无粘结滑移条件下,根据钢筋与混凝土变形协调
Δεc=Δεs(6)
Δεc=φ(t,t0)εe(t0)+εsh+(Δσc)/(Eφ)(7)
Eφ=(Ec(t0))/(1+χ(t,t0)φ(t,t0))(8)
上式中:Δεc和Δεs分别为混凝土和钢筋的应变变化,σc和σs分别为混凝土和钢筋应力,εsh是混凝土的收缩应变; Eφ是考虑混凝土时间效应的弹性模量.在混凝土应力不大于0.4倍混凝土抗压强度条件下,混凝土收缩徐变引起的内力应变变化满足Boltzman叠加原理,Tröst和Bazant通过引入χ(t,t0)老化系数概念,求得恒定荷载作用下混凝土结构中钢筋和混凝土的应力和应变变化(公式(9~11)),这种方法叫AEMM法[23].

最后,经过内力重分布之后,混凝土和钢筋的即时应力表达式为
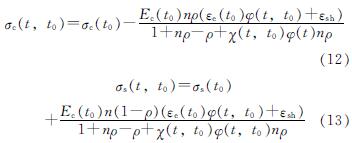
根据文献[12]建议,选取混凝土老化系数χ(t,t0)=0.8,基于上一节建立的考虑剪力墙应力重分布效应的收缩徐变分析模型,利用ACI209、B3、GL2000、CEB-FIP2010理论计算得到的结果与试验结果(取各竖向应变测点平均值)比较如图 10所示.各理论模型计算曲线与试验结果曲线变化趋势接近,其中,GL2000模型计算结果和试验曲线最吻合.
图 10 收缩徐变预测值与试验值比较
Fig.10 Comparison of shrinkage and creep strain between calculation and test results
图 11为根据上述截面内力计算模型得到的剪力墙内部钢筋和混凝土的应力随加载时间变化曲线,365 d加载时间内,混凝土应力由4.12 MPa降至3.79 MPa,应力松弛幅度为8.0%,钢筋应力由25.75 MPa增至64.41 MPa,增长幅度为150.1%,混凝土收缩徐变对纵向钢筋的受力状态有显著影响.
影响混凝土结构长期收缩徐变效应的因素较多,既包括混凝土力学性能、配筋率等结构内部因素,也包含加载龄期、荷载大小、环境湿度条件等外部因素,见表4.为比较这些参数对预制剪力墙长期收缩效应的影响,基于上文提出的竖向荷载作用下剪力墙收缩徐变计算模型,对十年服役期内剪力墙的应力应变变化进行了一系列计算分析比较.
分别对采用C30、C35、C40、C45四种不同强度等级混凝土的试件进行参数分析,其他的参数均为如表4所示基准参数.恒定竖向荷载作用下采用不同混凝土强度等级的剪力墙应变增量变化曲线如图 12所示,加载初期的三年时间内,剪力墙应变变化显著,随后计算周期内,剪力墙应变变化趋于平缓.随着混凝土强度等级的提高,由于高强度混凝土产生的收缩变形更小,相同周期内剪力墙的应变增量变化值呈现下降趋势.由表5可以看出,随着混凝土强度的提高,混凝土和钢筋的初始应力不变,混凝土应力变化不明显,钢筋的应力增长幅度减小.不同混凝土强度等级对应试件的应变比比值为1:0.933:0.883:0.840.因此,提高混凝土强度等级,可以一定程度上改善收缩徐变效应.
表5 不同混凝土强度试件混凝土和钢筋应力值
Tab.5 Strains of concrete and reinforcement of SRCSW with different strength concrete
以表4中的纵向配筋率0.5%作为基准值,分别比较纵向配筋率为1.0%、1.5%和2.0%的剪力墙的长期收缩徐变效应.由图 13和表6可以看出,在荷载恒定的情况下,配筋率增大,混凝土的初始应力降低; 经过长期收缩徐变,混凝土应力松弛幅度增大,0.5%配筋率试件混凝土应力下降幅度为7.2%,2.0%配筋率的试件混凝土应力下降30.8%; 不同配筋率构件应变比比值为1:0.957:0.918:0.883,钢筋应力终值比为1:0.963:0.929:0.897,试件应变增量随配筋率增大呈现减小趋势,这说明增大配筋量可以抑制剪力墙的收缩徐变变形.
根据表4中RH=85%环境湿度作为基准值,其他参数保持一致,分别比较75%、65%和55%环境湿度条件下剪力墙的长期收缩徐变变化.由表7和图 14可知,55%~85%环境湿度条件下对应的收缩徐变增量范围为-732.9~-340.8 με,环境湿度是混凝土试件收缩徐变变形的敏感因素,环境湿度越低,试件产生的收缩徐变效应越显著,相对应的钢筋应力增长幅度变化更加明显.值得注意的是55%环境湿度条件下,十年计算周期内,钢筋应力终值为169.9 MPa,增长幅度达548.5%.过大的应力增长可能使得剪力墙纵向钢筋突破设计强度值.因此,工程应用中需重点关注环境湿度对混凝土构件内力的影响.
表7 不同环境湿度下试件混凝土和钢筋应力值
Tab.7 Strains of concrete and reinforcement of SRCSW under different environmental humidities
保持其他参数与基准参数表4一致,初始加载龄期为14 d、28 d、60 d和90 d的受压剪力墙试件的应变及应力变化如图 15和表8所示,随着加载龄期的增大,剪力墙试件的收缩徐变效应减弱.由于龄期的增长,混凝土内部水化作用不断进行,收缩变形逐渐趋于平缓,相对收缩变形量逐渐减小导致试件应变增量减小.不同初始加载龄期试件对应的最终应变比比值为1:0.885:0.751:0.671,钢筋应力终值为1:0.915:0.815:0.757.因此,对于预制结构,预制构件在工厂内合理的前期养护对减少结构服役过程中收缩徐变效应有一定促进作用.
保持其他参数与表4一致,分别比较轴压比为0.1、0.2、0.3和0.4剪力墙的收缩徐变效应,对比分析结果如表9和图 16所示,各轴压比参数对应的瞬时弹性应变和应变增量分别呈现递增趋势,两者同竖向荷载变化成正相关关系; 当竖向荷载较小时,因瞬时弹性应变较小,长期荷载作用下的应变以收缩变形为主,较大的截面应力导致较大的瞬时弹性应变,应力水平提高,产生的应变增量更大,相应地,应变比比值呈下降趋势.
表8 不同初始加载龄期试件混凝土和钢筋应力值
Tab.8 Strains of concrete and reinforcement of SRCSW with different initial loading ages
表9 不同轴压比试件混凝土和钢筋应力值
Tab.9 Strains of concrete and reinforcement of SRCSW with different axial load ratio
(1)竖向荷载作用初期,预制叠合剪力墙预制层和夹心层竖向瞬时弹性应变接近,剪力墙整体工作性能良好.水平向瞬时弹性变形呈现轻微膨胀状态,预制层和夹心层瞬时弹性泊松比约为0.12,略低于混凝土材料的弹性泊松比;
(2)恒定竖向荷载作用下(12个月观测周期内),预制层和夹心层竖向徐变相近,应变增量与瞬时弹性应变比值约为1.6,与荷载方向垂直的水平向受拉徐变作用不明显,应变增量主要由混凝土收缩效应占主导;
(3)考虑长期竖向荷载作用下混凝土收缩徐变效应导致的剪力墙截面内力重分布,推导了剪力墙钢筋和混凝土应力应变计算公式,基于GL2000预测模型计算得到的剪力墙收缩徐变变形与试验结果最接近; 经过计算,试验周期内因长期收缩徐变效应引起剪力墙截面内力重分布,混凝土应力松弛幅度为8.0%,钢筋应力增长幅度为150.1%;
(4)通过参数分析,比较了混凝土强度等级、配筋率、环境湿度、初始加载龄期和轴压比变化对预制叠合剪力墙收缩徐变效应的影响.提高混凝土强度等级、配筋率可以降低收缩徐变作用; 随着龄期增长,混凝土收缩作用逐渐减弱,初始加载龄期越大,服役周期内结构的收缩徐变效应越弱; 因荷载作用导致的混凝土长期收缩徐变应变增量与轴压比增长呈递增关系; 环境湿度对收缩徐变效应影响最明显,环境湿度越低,收缩徐变变化越大,工程应用中需要重视较低环境湿度下混凝土结构中钢筋应力增长情况.