基金项目:国家自然科学基金(51778489); 国家科技支撑计划课题(2015BAK17B04); 科技部国家重点实验室基础研究资助项目(SLDRCE19A-02)
第一作者:陈 曦(1998—),男,博士生,主要从事工程结构抗震.E-mail: 2210009@tongji.edu.cn
通信作者:陈清军(1963—),男,教授,主要从事工程结构抗震.E-mail: chenqj@tongji.edu.cn
(1.同济大学 土木工程防灾国家重点实验室,上海 200092; 2.同济大学 结构防灾减灾工程系,上海 200092)
(1.State Key Laboratory of Disaster Reduction in Civil Engineering, Tongji University, Shanghai 200092, China; 2.Department of Disaster Mitigation for Structures, Tongji University, Shanghai 200092, China)
near-fault ground motions; pulse-like motions; vertical component; stochastic model; parameter identification
DOI: 10.15986/j.1006-7930.2023.02.002
近断层脉冲型地震动被认为是一类特殊的破坏性地震动,其时程内长周期速度脉冲包含大量能量,能在短时间内输入建筑结构并引发强烈振动,进而对结构产生巨大的破坏作用[1].虽然在过去的几十年中,国内外已采集到大量实测地震记录,但记录中具有脉冲特性的近断层地震动数量依然匮乏,现有近断层地震动记录难以满足近场工程结构抗震分析的需求[2].因此,许多学者开展了近断层地震动的模拟工作,并取得了诸多成果.贾路等[3]采用谱表示随机函数,提出了一种参数化的近断层脉冲型地震动降维模拟方法; Amiri等[4]提出了一种基于粒子群算法的神经网络和小波分析相结合的近断层地震动模拟方法; Dabaghi和Der Kiureghian[5]基于修正的M&P等效脉冲模型,提出了一种双向正交水平方向近断层地震动模拟方法.尽管如此,现有的研究成果仍然存在两个问题:一是为合理描述近断层地震动的特征,往往需要借助诸多参数,这给模拟方法的推广应用带来了诸多不便; 二是上述模型均为模拟水平地震动而进行校准,不适于竖向地震动分量的模拟.
已有研究表明,在结构抗震分析中不考虑地震动竖向分量可能会严重低估需求和高估能力,从而危及整体结构安全[6].近断层地震动往往具有较大竖向和水平峰值加速度比值,一般大于规范规定的2/3,甚至可以达到或超过1[7],所以对于近断层区域,更不能忽视竖向地震动作用.李宁等[8]从PEER中选取890组近断层强地震动,研究了地震动竖向与水平加速度峰值比与震级、断层距、场地条件间的统计规律; 潘毅等[9]以近断层竖向地震动为研究对象,开展了近断层区竖向抗震设计谱的研究.这些研究主要关注近断层竖向地震动的幅值及反应谱特征.
本文将首先从PEER强震数据库中选取100条典型近断层脉冲型地震动记录,形成近断层脉冲型地震动数据库.然后,将基于小波包变换的随机地震动模型与速度脉冲模型相结合,建立一种考虑竖向分量的脉冲型地震动随机模型.在此基础上,利用非线性规划方法进行模型参数识别,拟以NGA#1519地震动为例给出模型参数的识别过程,并选取典型走滑断层和逆断层地震动记录各一条,将模拟结果与实测记录进行对比以验证模型有效性.
本文采用Zhai C等[10]提出的基于能量的脉冲型地震动识别方法,从PEER强震数据库中选取了100条典型的近场脉冲型地震动记录.一条地震动时程被判定为脉冲型地震动需满足两个条件:一是地震动峰值速度PGV≥30 cm/s; 二是提取的速度时程的脉冲相对能量Ep>0.3.所选记录均具有完整的三向地震动时程,共由27次地震事件组成,包括了中强地震到高强地震(5.74≤Mw≤7.90)的地震震级,地震记录所在场点破裂距离均不超过30.2 km(Rrup≤30.2 km),断层机制包括走滑断层(SS)和逆断层(RV/RO)两类,同时为保证合理的样本数量,没有对选取记录所在台站的场地等效剪切波速VS30做限制.图1给出了所选地震动断层机制、Mw、Rrup和VS30的分布关系,表1给出了数据库内地震动记录的基本信息.
图1 脉冲型地震动记录与断层机制、Mw、Rrup和VS30的分布关系
Fig.1 Distribution of pulse-like ground motions with respect to type-of-faulting, Mw、Rrup和VS30
基于简化速度脉冲模型和随机性模型组合的混合模型,是目前国内外学者广泛采用的脉冲型地震动模拟方法.确定性的简化速度脉冲模型可充分描述近断层地震动低频脉冲特性,随机性方法较好的考虑了地震动时域和频域的非平稳特性,可有效实现地震动高频分量模拟.
本文采用Dickerson和Gavin[11]提出的脉冲模型,该脉冲模型数学表达式为
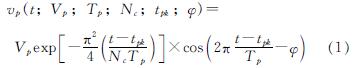
式中:vp表示所提取的速度脉冲时程.它由五个参数完全定义:脉冲幅值Vp、脉冲周期Tp、脉冲所含半波循环数Nc、脉冲发生时刻tpk以及脉冲相位φ.该模型数学表达式相对简单,且模型参数具有明确物理意义.
剔除脉冲后的近断层地震动残余时程通常为一宽频时间序列,具有缓慢演化的时间和频谱特征.Li YN等[12]提出的基于小波包变换的随机地震动模型可用于模拟这些宽频运动.模型通过三个时间非平稳参数Td、ε、η,两个频率非平稳参数μ、σ和一个幅值调整参数APGA,共计6个参数实现了时频全非平稳地震动的模拟.图2给出了模拟方法的基本流程:(a)生成一段时间长度为Td的高斯白噪声序列;(b)采用Saragoni函数加窗,生成强度非平稳加速度时程;(c)对时间序列进行小波包分解获得小波包系数矩阵;(d)假定真实地震动时变频率服从对数正态分布密度函数(LNDD),并使用不同的LNDD对小波包系数矩阵列向量进行调整;(e)利用小波包重构将小波包系数矩阵变换回时域,并将加速度幅值按照APGA进行调整.
本文在最大水平脉冲方向上ah(t)和垂直方向av(t)建立了脉冲型地震动模型,ah(t)内共包含两个子模型:一个模型用于模拟低频脉冲apul(t),另一个模型用于模拟剩余时程ares(t),即总时程减去脉冲时程.apul(t)使用参数为Vp、Tp、Nc、tpk、φ的Dickerson-Gavin脉冲模型进行模拟,由于每一条脉冲时程均满足Nc=1以及φ=0的条件[15],因此最终仅需Vp、Tp、tpk三个参数便可以实现对apul(t)的模拟; ares(t)使用参数为Td、ε、η、μ、σ、APGA的小波包随机模型进行模拟.
通过对脉冲型地震动竖向分量的观察与统计分析,数据库内74%的竖向地震动被判定为不含速度脉冲,其中,73%的竖向地震动不满足PGV>30 cm/s的条件,26%的竖向地震动不满足脉冲相对能量Ep>0.3的条件.尽管如此,统计结果也表明竖向地震动中包含了较多的低频成分,在模拟过程中是不能忽略的,采用Dickerson-Gavin模型仍然可以进行较好的提取与模拟.所以,为保证水平及竖向地震动模型形式的一致性,av(t)采用与ah(t)相同的两个子模型分别模拟低频成分与高频成分,并定义低频加速度时程用aver1(t)表示,高频加速度时程用aver2表示.因此,本文所使用的多分量脉冲型地震动模型采用表2所示的18个参数完全定义,分别表示为αi,t=1,…,18.
表2 多分量脉冲型地震动模型参数αi,i=1,…,18
Tab.2 Model parameters of multi-component pulse-like ground motion
首先对模型参数Vp、Tp、tpk和Vv、Tv、tvk进行识别,并计算出相应的剩余时程.在拟合过程中,Vp认定为与最大峰值速度(PGV)在时域内重合且相等,脉冲发生时刻tpk也因此确定; 同时定义脉冲时程为一个完整的循环脉冲,即Nc=1,并认为大多数情况下符合脉冲相位φ=0的假定,最后依照拟合时程与实际速度脉冲波形间平方差最小化原则识别脉冲周期Tp,采用最小二乘法实现这一过程.图3中以1999年台湾集集地震TCU103台站(NGA#1530)E-W方向和垂直方向的两条地震波时程作为目标地震动,给出了模型参数的识别过程,该地震事件基本信息为:Rrup=6.08 km,VS30=494.1 m/s,Mw=7.62.
为消除实际记录初始噪声和尾部噪声对模拟结果的不良影响,Thd和Tvd分别取为高频时程ares(t)和aver2(t)的1%和99% Arias强度水平对应时刻的差值.此时,1% Arias强度水平对应时刻t1%为模拟时程的初始时刻,因此需对已识别参数tpk和tvk做相应调整.根据Saragoni窗函数的Arias强度曲线与目标记录的Arias强度曲线的最佳拟合,确定参数ε、η的取值.一组模型参数ε、η所对应模拟记录的强度曲线可根据以下公式计算.
Iα(t)=∫t0α2(τ)dτ(2)
Ariassim(t,ε,η)=E[Ia(t)]=∫t0E[a2(τ)]dτ
=∫t0w(τ,ε,η)2dτ(3)
式中:a(τ)为目标地震动加速度时程,w(τ,ε,η)为使用ε、η定义的Saragoni窗函数.将目标函数定义为模拟和目标Arias强度差的平方,得到
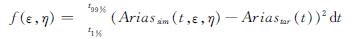 (4)
(4)
利用MATLAB函数“fmincon”和序列二次规划(SQP)算法求出ε、η的最优解,使f(ε,η)最小.图4(a)给出了NGA#1519地震动水平向模拟时程和目标记录的Arias强度曲线.
通过选择与实际地面运动功率谱相匹配的适当值进行μ、σ的参数识别.对于随机方法,每次产生的高斯白噪声是不同的,所以使用相同的μ、σ生成的功率谱也会略有不同.获得参数ε、η后,生成若干样本时程并计算相应的小波包系数矩阵.利用调幅后的小波包系数矩阵估计功率谱密度并定义如下目标函数.
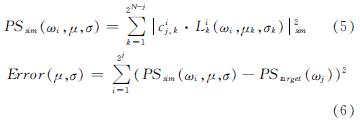
式中:cij,k表示在第j层分解时小波包系数矩阵第i行中的第k个小波包系数; Lik(ωi,μk,σk)表示对第k列向量进行归一化的LNDD函数.上述过程同样采用SQP算法求出使Error(μ,σ)取最小值时μ、σ的解.图4(b)给出模拟时程和目标记录的功率谱曲线.
参数APGA定义为剔除低频时程后剩余时程的加速度幅值而非实测地震动的加速度幅值,该参数的识别可方便通过编程实现,因此不再赘述.
为展示采用该模型进行地震动模拟的有效性,图5、图6分别选取NGA#170和NGA#1480作为典型走滑断层和逆断层地震动记录,给出了模拟时程与原始记录水平及竖直方向的加速度时程、速度时程与加速度反应谱的对比图.表3给出了两条地震动的基本信息.模拟的时间序列的步长dt=0.01 s,小波包分解层数j=8,以保证对低至0.2 Hz频率的合理控制.结果表明本文模拟方法能准确捕捉实际记录的时频特征,同时较好的匹配了实际记录的加速度反应谱.
本文选取典型近断层脉冲型地震动记录,形成近断层脉冲型地震动数据库; 将小波包变换的随机地震动模型与速度脉冲模型相结合,建立了一种考虑竖向分量的脉冲型地震动随机模型.利用非线性规划方法进行模型参数识别,并选取典型走滑断层和逆断层地震动记录各一条,在加速度时程、速度时程与加速度反应谱等方面将实际地震动与模拟结果进行对比,验证了模型有效性.
本文建立的考虑竖向分量的脉冲型地震动随机模型,在水平向和竖向各使用9个参数、共计18个参数对近断层地震动时频特征、非平稳性及脉冲特性进行合理表达.分析结果表明:这一模型可以对近断层区域的水平向及竖向地震动进行有效模拟; 本文给出的模型参数识别方法可在时域上和频域上均获得与目标地震动相匹配的结果.这为后续开展基于地震场景的模型参数回归和指定震源特征的近断层地震动模拟等相关研究奠定了基础.