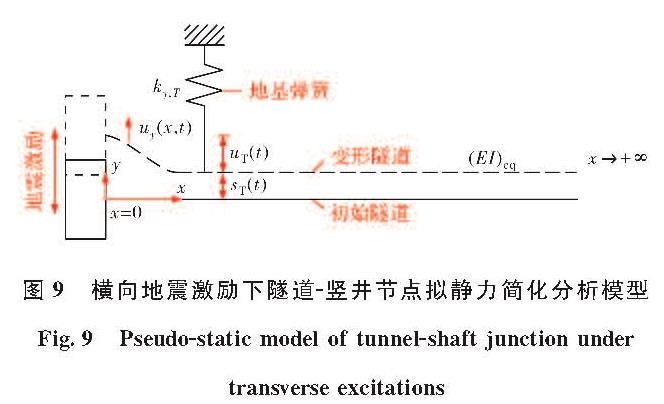
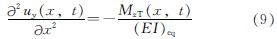1.1 试验方案
本试验利用同济大学地震工程馆多功能振动台系统,台面长10 m,宽6 m,额定输出加速度1.5 g,额定荷载140 t.工程原型盾构隧道外径15 m.考虑试验中隧道模型与模型箱侧壁应留出大于10倍隧道直径的宽度以消除边界效应,可初步选定试验缩尺比例为1:60.试验中拟采用上海人工波为地震激励信号,考虑台面额定输出加速度限制,可初步选定惯性加速度相似比为4:1.
隧道地震动力响应主要受土-结构动力相互作用控制[10].因此,模型场地的动力特性相似,是试验方案设计的首要内容.已知连续固体动力运动方程如下[11].
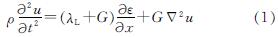
式中:ρ为密度; u为位移; t为时间; λL为Lame常数; G为剪切模量; ε为应变; x为位置坐标.由此,可选定密度ρ,位移u,剪切模量G为模型场地相似基本变量,并由量纲分析可得如下相似关系为
SG/(Sl·Sρ)=Sa(2)
在几何相似比Sl和惯性加速度相似比Sa已选定的前提下,剪切模量相似比SG和密度相似比Sρ符合上述方程的材料可用于制作本试验中的模型场地.已知工程原场地等效均一重度为19.1 kN/m3,等效最大动剪切模量为116 MPa.因此,可选用锯末和干砂按1:2.5质量比配置而成的人工土模拟隧道原场地[12].由此可得本试验相似关系如表1所示.
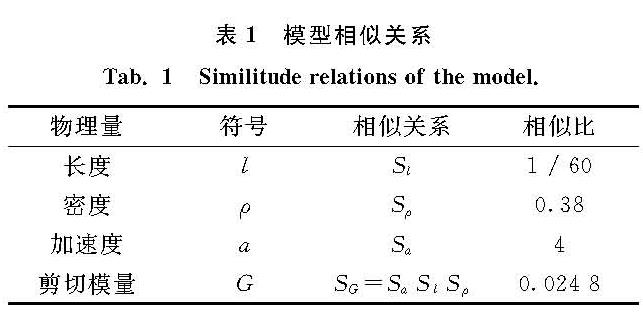
表1 模型相似关系
Tab.1 Similitude relations of the model.
地下结构抗震分析的特点在于其地震响应主要受土-结构动力相互作用的控制[10],其中土-结构相对刚度比为隧道地震响应的关键控制变量[13-14].因此,本试验选取土-结构相对刚度为控制指标进行隧道模型的设计,即原状土和原型结构的土-结构相对刚度比与模型土和模型结构的土-结构相对刚度比保持一致,可使模型系统与结构原型的土-结构动力相互作用尽可能一致.圆截面隧道的土-结构相对弯曲刚度比如下[10].
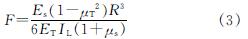
式中:F为隧道横断面土-结构相对弯曲刚度比; Es为土体弹性模量; μT为隧道泊松比; R为隧道半径; ET为隧道弹性模量; IL为单位长度隧道横断面相对隧道轴线的惯性矩; μs为土体泊松比.由方程(3)可得隧道模型相似比控制方程为
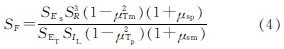
式中:μTm为隧道模型泊松比; μsp为原场地泊松比; μTp为原型隧道泊松比; μsm为模型土泊松比.已知隧道原型采用C60混凝土浇筑,弹性模量为36 GPa,泊松比为0.167.原状土泊松比为0.38,模型土泊松比为0.40.因此,可选用聚乙烯材料制作隧道模型,其弹性模量为790 MPa,泊松比为0.41.又SR=Sl=1/60,可得SF=0.95,接近目标值1.此外,聚乙烯材料还有价格低廉,易于高精度加工等优势.
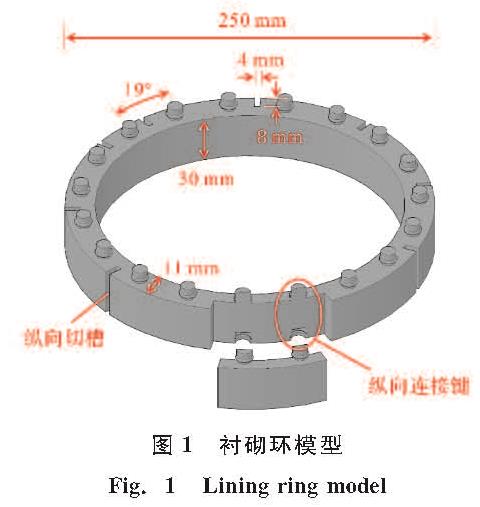
为模拟盾构隧道管片拼装的效果,本试验隧道模型由独立衬砌环模型拼装而成.如图1所示,每个衬砌环宽30 mm,外径250 mm,厚11 mm.衬砌环间通过纵向连接键互相咬合,以此模拟环缝和纵向螺栓连接.在原隧道纵缝位置处,设置纵向削减槽,以此模拟纵缝和环向螺栓连接.为精确还原竖井内部构造,采用3D打印快速成型技术,按1/60缩尺比例制作竖井模型,如图2所示.
图1 衬砌环模型
Fig.1 Lining ring model
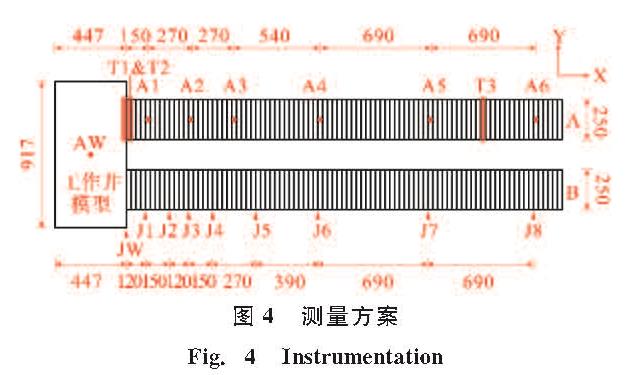
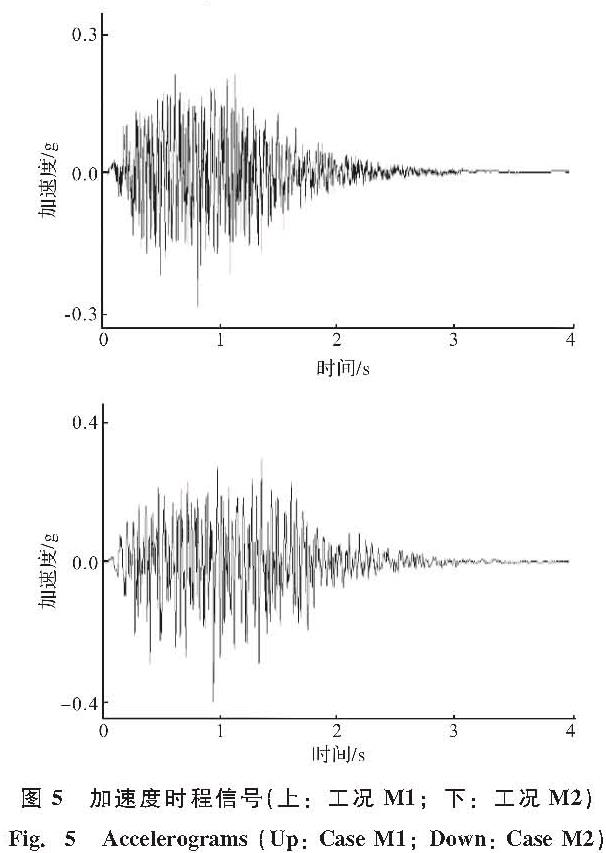
本试验采用刚性箱为模型容器.如图3所示,模型箱长10 m,宽4.5 m,高1.5 m.试验测量方案如图4所示,隧道模型A上设置A1~A6共6个加速度测点,竖井模型上设置AW加速度测点,均用于测量沿隧道横断面方向的加速度响应.隧道模型B上共设置9个环缝张开量测量面,即图4中JW和J1~J8.以上海人工波为台面输入激励,振动方向沿隧道横断面方向.工况M1中,台面峰值加速度0.3 g,50年超越概率10%.工况M2中,台面峰值加速度0.4 g,50年超越概率3%.加速度时程信号见图5.
图3 振动台试验
Fig.3 Shaking table test
图4 测量方案
Fig.4 Instrumentation
图5 加速度时程信号(上:工况M1; 下:工况M2)
Fig.5 Accelerograms(Up: Case M1; Down: Case M2)
1.2 试验结果及分析
分别提取两工况中各测点加速度响应峰值,如图6所示.竖井测点AW均记录到相应工况中加速度响应最大值,图中曲线从左到右沿远离竖井方向均逐渐减小.为了更准确地定量描述隧道和竖井间的差动响应,采用统计学方法,计算工况M1中不同测点加速度信号相关系数为
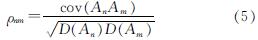
式中:An和Am分别为n测点和m测点记录到的加速度时程信号; cov(An,Am)为An和Am的协方差; D(An)和D(Am)分别为An和Am的方差; ρnm为An和Am的相关系数.采用以上公式算得相关系数矩阵如图7所示,矩阵中各元素对应各测点加速度信号相关系数.例如,矩阵中第一行第三列元素为AW测点和A2测点的加速度信号相关系数.相关系数取值范围为-1~ +1,其中-1代表严格负线性相关,+1代表严格正线性相关,0代表不相关.由定义可知,所有相关系数矩阵均为对称矩阵,且对角线元素为1.
图6 加速度响应峰值
Fig.6 Peak acceleration responses
图7 工况M1加速度信号相关系数
Fig.7 Correlation coefficients of acceleration in Case M1
图7中,所有相关系数均大于0.79,说明隧道-竖井整体响应相似.其中最小元素为竖井测点AW和隧道测点A6间的加速度响应相关系数.并且,所有小于0.90的相关系数,仅出现在矩阵的第1行(列),而隧道测点A2~A6间的相关系数均不小于0.96.由以上分析可知,尽管隧道-竖井整体跟随地层运动,但两者仍有明显的差动响应,不仅加速度响应峰值有差异,且加速度信号整体相关性较弱.
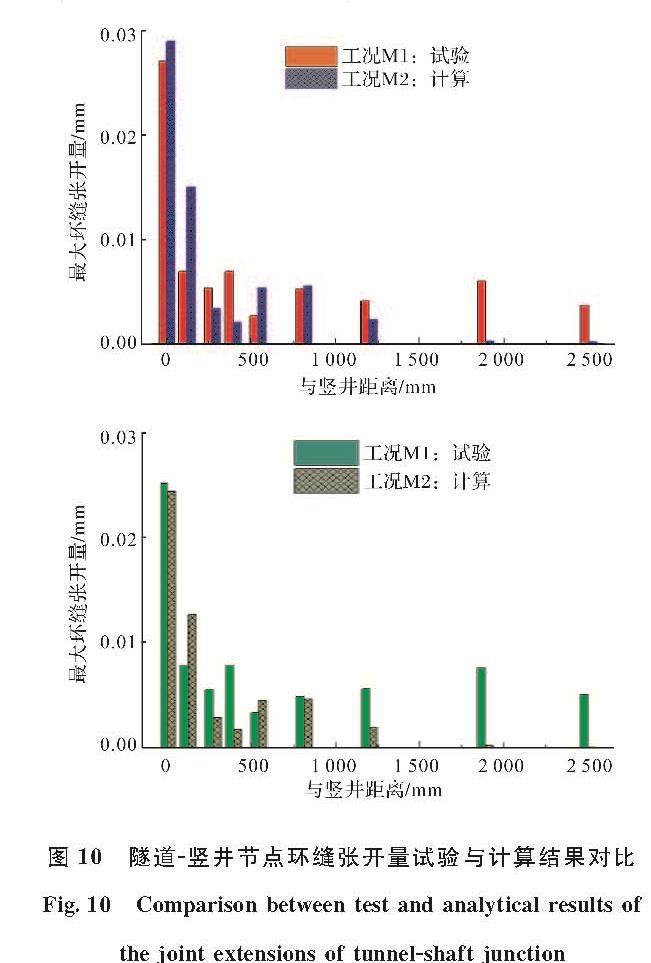
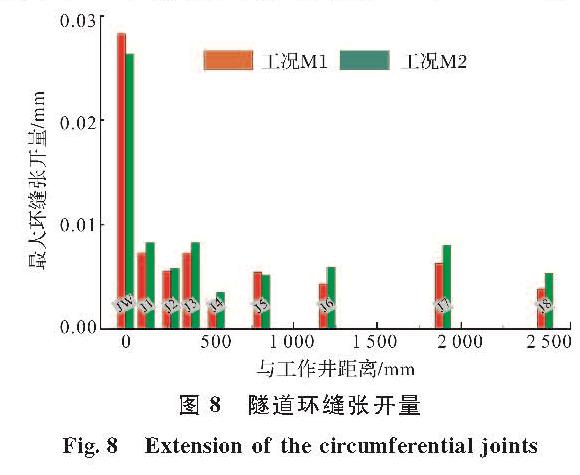
分别提取两工况中各环缝测量面记录到的峰值张开量,如图8所示.其中,隧道与竖井对接环缝JW均记录到张开量最大值.从JW到J8,沿远离竖井模型方向,环缝张开量呈现明显的下降趋势.与距离竖井模型最远的J8相比,M1和M2工况中,JW环缝张开量分别增加642%和396%.
图8 隧道环缝张开量
Fig.8 Extension of the circumferential joints
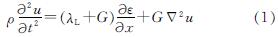
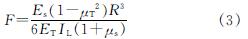
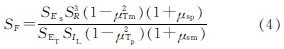


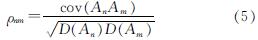


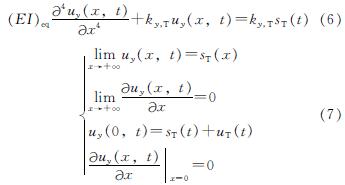
 (8)
(8)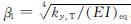 .又欧拉-伯努利梁有如下挠度-弯矩关系,即
.又欧拉-伯努利梁有如下挠度-弯矩关系,即