基金项目:国家自然科学基金(U1710111 & 51878426); 中国博士后基金面上资助项目(2021M700096); 中央高校基本科研业务费专项资金项目
第一作者:周裕洲(1994—),男,硕士,工程师,主要从事工程结构抗震研究.Email: SCUyuzhou@outlook.com
通信作者:王健泽(1990—),男,博士,副研究员,主要从事工程结构抗震研究. E-mail:jzwang@scu.edu.cn
(1.四川大学 土木工程系,四川 成都,610065; 2.彭州市住房和城乡建设局,四川 成都 611930; 3.四川二八二核地质工程公司,四川 成都 618000)
(1.Department of Civil Engineering, Sichuan University, Chengdu 610065,China; 2.Pengzhou Housing and Urban-Rural Development Bureau,Chengdu 611900,China; 3.Sichuan 282 Nuclear Geological Engineering Company,Chengdu 618000,China)
elevated steel storage silo; silo storage; nonlinear floor response spectrum; shaking table test; spectrum standardization
DOI: 10.15986/j.1006-7930.2023.02.005
建筑结构中包含的非结构构件与安装在结构中的附属机电设备统称为非结构构件[1].随着建筑工程结构防灾减灾学科研究的快速发展,现行设计标准与规范足以确保建筑结构主体的安全,但作为建筑主体结构以外的非结构构件,在地震中的损害尤为严重[2].储仓结构是广泛应用于工业生产材料贮存的通用性构筑物,尤其在煤炭、建材、冶金等系统中应用较为普遍.重型储仓具有体积大,且储仓质心与储料存储量相关的特点,在地震作用下对其支承结构产生较大惯性力效应,易对主体结构造成破坏.1995年发生在日本兵库县的7.2级地震,导致一钢板筒仓局部屈曲倒塌,1999年发生在土耳其北部的7.2级地震,导致一水泥储仓倒塌[3].因此,从以往震害经验来看,对含重型储仓的工业结构进行合理的抗震设计与防护尤为重要.
楼面反应谱方法是非结构构件抗震设计常见的方法,通常获取楼面反应谱的做法是将与目标谱相匹配的地震动输入结构,采用时程分析方法得到楼层对应位置的绝对加速度时程,按照经典反应谱理论生成对应楼层的楼面反应谱,即反应谱-时程-楼面反应谱的方法,此方法可以计算出目标结构在地震作用下较为准确的动力响应,但需要对每一积分步进行迭代计算,故该方法计算耗时较长.楼面反应谱生成的另一种方法是通过输入结构的地震设计谱直接生成对应楼层的楼面反应谱,即反应谱-楼面反应谱方法,该方法避免了复杂的时程计算,但是难以考虑非线性响应的影响[4-5].从已有研究来看,关于楼面反应谱生成方法的研究发展主要经历了两个阶段,即传统楼面反应谱和新型楼面反应谱.传统楼面反应谱是强行将结构与设备解耦,得到设备所在楼层位置处的楼面反应谱并用于设备抗震设计,前提要求是设备与所在楼层的质量比小于0.1%,且互相不发生调谐,而解耦的处理方法使分析结果忽略了设备自身的动力特性以及与结构之间的相互作用.随着楼面反应谱研究的发展与科学计算能力的提高,新型楼面反应谱分析要求合理考虑设备自身的动力特性以及两者之间的相互作用等因素的影响[6].
早期楼面反应谱的提出是由于核电设备需要寻找合理的地震输入源.有学者根据经验得到地震动力放大系数,直接生成对应楼层的楼面反应谱,但该方法计算得到的结果偏于保守[7].有学者基于随机振动理论生成楼面反应谱,但是计算方法较为复杂,故该方法目前没有广泛应用到工程中[8-12].Suarez[13]等基于模态叠加理论,考虑主结构与附属设备之间的相互作用,得到对应楼层的楼面反应谱.Yasui[14]等提出了一种基于特定假设条件下所得到的楼面反应谱近似算法.蒲武川[15]等基于Yasui的理论对该方法进行修正,通过引入修正参数得到单自由度/多自由度结构楼面反应谱的直接计算方法.
然而,已有文献对于本研究涉及的这类层间设备与结构质量比较大,且质量比变化严重影响结构自身动力特性的重型设备楼面反应谱研究甚少,部分研究考虑了非结构构件各类参数变化对楼面反应谱的影响.因此,本文主要对工业建筑中常见的含重型储仓设备结构的楼面反应谱进行研究,建立了设备-结构耦合模型,通过对比研究储仓在不同装载量下的非线性楼面反应谱的特点,提出了适合重型储仓楼面反应谱的标定方法,同时结合振动台试验验证其合理性,为今后非线性楼面反应谱近似求解提供理论基础.
本研究以某实际800 MW燃煤机组火电厂中65.8 m高的高架式燃煤储仓结构为研究对象.主体结构与储仓的几何信息和各层荷载质量分布如图1所示.储仓上圆段高25.5 m,内径8.8 m,下部漏斗段高9.2 m,总容积为1 713 m3,大约是常规百万机组储煤量的2倍,由《钢筒仓技术规范》GB50884—2013[16]定义可知,该筒仓属于深仓式.该储仓放置于建筑标高31.4 m位置处.不同装载量下储仓质量与结构总质量的比值差异较大,如表1所示.根据《建筑抗震设计规范》(GB50011—2010)[1]进行抗震设计,该厂房所在场地设防烈度为8.5度,设计地震加速度为0.3 g,所在场地为III类,地震分组为第二组.
图1 储仓-主体结构几何信息与有限元模拟示意图
Fig.1 Schematic diagram of silo-main structure geometric information and finite element simulation
本研究采用大型通用有限元软件ANSYS进行建模计算,其中梁、柱、支撑均采用Beam188单元模拟,通过Mass21单元将布置的恒荷载与活荷载转化为节点质量.梁和柱构件采用共享节点的方式实现刚性连接.为模拟支撑受压屈曲特性,通过在支撑中点位置设置长度为1/1 000初始构件长度的面外初始缺陷[17].对于储仓设备部分,储仓壁板采用Shell181进行模拟,储仓加劲肋采用Beam188模拟[18].加劲肋的梁单元与储仓壁板的壳单元之间采用刚性连接.通过MPC184建立主结构与储仓之间的连接[18].主体结构与储仓均采用Q345钢,屈服强度为345 MPa,模型材料密度取8 000 kg/m3,材料杨氏模量取200 000 MPa,泊松比为0.3.数值模拟中,采用双线性等向强化模型模拟材料非线性,其中屈服后刚度为屈服前刚度的0.01倍.
根据研究需要共建立了空仓、20%装载量、50%装载量、60%装载量、70%装载量、80%装载量、90%装载量、满仓共8个不同装载量的设备-结构一体化模型开展模态分析,如表2所示.通过对设备-结构一体化模型振型的研究发现,八个模型一阶振型(Mode 1)为Y方向平动,二阶振型(Mode 2)为X方向平动,三阶振型(Mode 3)为扭转,说明储仓装载量变化对结构主要振型基本没有影响.通过对不同装载量的设备-结构一体化模型自振周期的研究可知,储仓中装载量的变化明显改变储仓-结构耦合模型的自振周期,其中一阶自振周期与二阶自振周期改变明显,分别从1.33 s变化到1.84 s和1.18 s变化到1.72 s,而扭转振型对应的自振周期变化相对较小,从0.78 s变化到0.92 s.此外,储仓装载量的增加对结构前三阶模态所对应的质量参与系数影响不大.
根据《建筑抗震设计规范》(GB50011—2010)生成的加速度设计反应谱作为目标谱,通过目标谱在PEER-NGA网站[19]上选取18条地震动.选取地震动与目标谱的匹配情况如图2所示.对于本研究中采用直接积分的时程分析方法,采用基于Newmark的隐式算法求解,通过双线性等向强化模型考虑材料非线性,通过开启软件中的大变形功能考虑结构分析中所存在的所有几何非线性.分析阻尼采用瑞利阻尼,阻尼模型参数按照第一周期与第二周期3%阻尼比进行计算.
提取储仓支承位置的绝对加速度时程,转化为对应支承位置的楼面反应谱,如图3所示,其中图3(a)~(h)为储仓不同装载量下的楼面反应谱.结果表明,8个模型所得到的非线性楼面反应谱具有两个较为明显的峰值平台段.高频段位置的双峰与结构高阶振型和输入地震动平台段有关,且伴随储仓装载量的增加,第一个峰值逐渐向右偏移,峰值从0.16 s增加到0.28 s,而第二个峰值基本保持不变,在0.50 s到0.60 s之间.中低频段峰值受结构第二阶振型影响,且随着储仓装载量增加导致的非线性发展,使结构整体刚度发生退化,该峰值逐渐向右发生偏移,峰值出现位置从1.38 s变化到2.14 s.随着储仓装载量的增加,楼面反应谱的峰值下降明显,高频段第一个峰值从11.94 m/s2下降到5.96 m/s2,第二个峰值从8.85 m/s2下降到5.11 m/s2,中低频段峰值从空仓状态的12.39 m/s2下降到满仓状态的6.68 m/s2.导致峰值呈现下降趋势的主要原因是结构进入非线性程度增加,进一步过滤了地震动高频能量在结构中的传播.
对已有的不同装载量下重型储仓楼面反应谱高频峰段与中低频段分析可知,重型储仓楼面反应谱存在两个较为明显的峰值平台段,本研究基于标准化设计反应谱思路采用最小二乘法进行构建,如公式(1)和图4所示.其中:Te,1与Te,2分别为第一平台段第一与第二拐点; Ts,1与Ts,2分别为第二平台段第一与第二拐点; βmax,1与βmax,2分别为第一平台段与第二平台段的动力放大系数.参考《GB 50267-2019 核电厂抗震设计标准》[20],对于子系统阻尼比小于10%,按照规定可将楼面反应谱削峰15%,同时拓宽峰值对应的频率区间后作为设计楼层反应谱使用,即βmax,1与βmax,2取值为相应峰值的85%,Ts,1和Ts,2分别取第二峰值周期的0.85倍和1.15倍.由于Te,1与Te,2取值与结构高阶振型和输入地震动平台段有关,受储仓装载量变化影响较小,在拓宽峰值频率中发现其数值相对固定,故在实际标定过程中高频双峰对应平台段可直接取0.22~0.58 s.
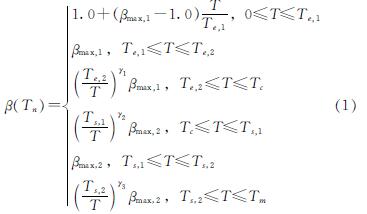
公式(1)中的γ3由第二平台段右侧下降段采用最小二乘法拟合得到.γ1、γ3和Tc需要由第一平台段右侧下降段和第二平台段左侧上升段采用多段函数拟合的方式得到,并且需要合理控制Tc的线性搜索范围在Te,2与Ts,1之间以达到理想的拟合效果.按照上述方法生成拟合的楼面反应谱如图5所示.
本文以不同储料装载量的某高架式钢储仓结构为研究对象,以18组与目标谱匹配的地震动为输入,通过对设备-结构耦合模型开展弹塑性时程分析,分析储仓支承位置的非线性楼面反应谱,并借鉴标准楼面反应谱标定方法,提出重型储仓楼面动力放大系数的标定方法,同时借助振动台试验验证其合理性,主要得出以下结论:
(1)储仓装载量的变化对结构X、Y方向一阶自振周期影响较大,而结构主要振型保持不变,自振周期与其对应的质量参与系数差异较小.
(2)重型储仓楼面反应谱高频段位置的双峰与结构高阶振型和输入地震动平台段有关,且伴随储仓装载量的增加,第一个峰值逐渐向右偏移,而第二个峰值基本保持不变.中低频段峰值受结构第二阶振型影响,且储仓装载量增加导致的非线性发展导致结构整体刚度退化,该峰值逐渐向右发生偏移.
(3)采用最小二乘方法结合标准反应谱的形式,并提出适合双峰、多峰特性的非线性楼面设计谱的标定方法,并采用振动台试验验证了其适用性,同时为今后非线性楼面反应谱近似求解提供理论基础.