基金项目:国家重点研发计划资助(2022YFC3004300); 中国博士后科学基金资助项目(2021M700311); 北京市博士后国际交流培养资助派出项目(2022-PC-03)
第一作者:张 卜(1990—),男,博士,助理研究员,主要从事隧道及地下结构抗震研究. E-mail: zhangbu@bjut.edu.cn
通信作者:钟紫蓝(1986—),男,博士,副研究员,主要从事地下结构抗震研究. E-mail: zilanzhong@bjut.edu.cn
(1. 北京工业大学 城市建设学部,北京 100124; 2. 北京工业大学 城市与工程安全减灾教育部重点实验室,北京 100124)
(1.Faculty of Architecture, Civil and Transportation Engineering, Beijing University of Technology, Beijing 100124, China; 2. Key Laboratory of Urban Security and Disaster Engineering, Ministry of Education,Beijing University of Technology,Beijing 100124, China)
seismic resistance of underground structures; shaft seismic response; shaft lining; elastic foundation rod
DOI: 10.15986/j.1006-7930.2023.02.006
目前,我国地下空间工程发展迅速,且已有地下结构震害表明,地下结构在地震中亦会受到损坏,为保证其安全,需要对地下结构进行充分抗震设计[1-6].地下结构动力响应受到周边土体控制,地基土变形是地下结构震害的主要诱因[7-8].竖井作为地下基础设施工程,是地上与地下结构联系的“纽带”,在调节地下结构的气压、通风换气及防灾救援等方面发挥着重要作用[9-10],其在地震中遭受破坏后会发生衬砌开裂和渗漏水等难以修复的问题,因此,明确竖井初衬和二次衬砌组成系统在地震下的动力响应对竖井结构抗震设计具有重要意义.
竖井与隧道结构分别作为竖直线状与水平线状两种常见地下结构形式,其中隧道抗震研究较为成熟,可为竖井研究提供借鉴意义,隧道的地震响应研究方法主要采用理论解析、数值模拟和模型试验[11].Zhong等[12]研究了隧道在断层运动引起断层裂隙带变形作用下的性能; Kirzhner等[13]分析了隧道围岩在地震作用下的动力响应; Amorosi等[14]建立二维有限元模型研究了黏土中圆形隧道的横向动力响应; Wang等[15]分析了厚膨胀土层中隧道衬砌的地震响应; 袁勇等[16-17]、禹海涛等[18]使用振动台模型试验研究了长大隧道在非一致激励下的地震响应机制.由于数值模拟技术要求相对较高,模型试验周期较长,许多学者通过解析解推导进行分析,Park等[19]研究了圆形隧道衬砌在地震作用下椭圆形变形时的力与力矩解析解; 禹海涛[20]推导了均质地层长隧道纵向地震响应解析解; 张栋梁[21]推导出地震中自由场土体剪应变最大时刻土-结构间不滑移和完全滑移两种接触条件下圆形衬砌动内力的解析解.
对于竖井结构抗震研究,Zhang等[22-24]对线弹性地层中文克勒地基模型下竖井的地震响应提出了理论解析解,基于拟静力法推导了名义柔度比公式评估竖井动力响应特征,并采用三维动力时程分析方法研究了上海软土中的大型竖井地震响应; Zhang等[25-27]提出了在横向荷载作用下竖井与隧道接头处隧道和竖井分别的动力响应解析解,推导了SH波下竖井-隧道接头处的地震响应解析解; Mayoral等[28]对黏性土条件地震作用下竖井结构损伤曲线进行了研究; Kim等[29]采用动力分析方法和拟静力分析方法对竖井及其周围土体之间的荷载传递机理和动力响应进行了数值分析; Guerra等[30]提出一种新数值模型研究大直径混凝土衬砌竖井在地震激励下的响应; 陈向红等[9]针对深水中的隧道竖井,推导了软土地基中结构的动力平衡方程并进行求解; 申玉生等[10]分析了穿越上软下硬地层公路隧道竖井结构抗震性能.结合以上已有隧道和竖井抗震研究发现,已有研究主要集中于单个竖井结构地震响应分析,缺乏同时考虑竖井初衬和二次衬砌相互作用的竖井地震响应研究,亟需推导并建立地震作用下竖井初衬和二次衬砌动力响应解析解.
本文基于分布传递函数法基本理论[31],采用广义位移法的基本思想[32],即竖井的地震响应受到周围地层响应控制,将周围地层与竖井结构初衬和二次衬砌简化为相互作用的文克勒地基杆系统,推导了地震作用下二者竖向动力响应闭式解析解,并将其与有限元法数值解进行对比验证,最后从地基弹簧刚度、二次衬砌刚度和竖井外径的角度出发分别对初衬和二次衬砌顶部位置竖向位移地震响应进行参数化分析,得出一定规律,研究方法和结论可为竖井抗震设计提供一定参考,并为今后竖井的抗震研究提供理论方法和科学依据.
本文将竖井结构初衬及二次衬砌简化为两根平行可竖向振动的杆,初衬周边土层简化为文克勒粘弹性地基,其中均匀分布的弹簧和阻尼器分别模拟竖井周围土体的动切向刚度和辐射阻尼,假设初衬与二次衬砌之间切向为弹性连接,忽略法向作用,将其简化为均匀分布的切向弹性连接层,竖井的初衬与二次衬砌构成了一个文克勒地基杆系统,其简化计算模型如图1所示.其中初衬简化为杆1,二次衬砌简化为杆2.杆1的抗拉刚度为E1A1,等效线密度为ρ1; 杆2的抗拉刚度为E2A2,等效线密度为ρ2; 侧向土层分布弹簧刚度为Ke,辐射阻尼系数为Cs; 杆1与杆2之间切向弹簧刚度为K,竖井的长度为L.在地震动激励作用下,初衬简化杆的竖向位移响应为w1(z,t),二次衬砌简化杆的竖向位移响应为w2(z,t).
计算分析时的简化假定如下:①竖井初衬和二次衬砌为各向同性并且均质的线弹性体; ②初衬与二次衬砌顶部为自由端,底部假设为弹性边界,通过弹簧和阻尼器与场地连接; ③地震激励为垂直入射的P波,在地震激励作用下土层自由场产生竖向位移响应,竖井初衬和二次衬砌在自由场位移作用下随之产生竖向位移响应.
地震波垂直入射引起的自由场位移施加在竖井上,使得初衬与二次衬砌组成的文克勒地基杆系统产生响应,在简化模型中将地震位移作用于粘弹性地基远离结构的一侧,以此模拟文克勒地基杆系统在地震作用下的响应.取系统中微元体进行力平衡分析,容易得到以下两个耦合的微分控制方程为
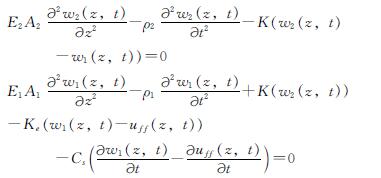 (1)
(1)
式中:w1(z,t)为杆1的竖向位移; w2(z,t)为杆2的竖向位移,E1为杆1的弹性模量; E2为杆2的弹性模量,A1为杆1的面积; A2为杆2的面积,ρ1和ρ2分别为杆1和杆2的等效线密度,K为杆1和杆2之间的切向弹簧刚度,Ke为土层分布弹簧刚度,Cs为辐射阻尼系数,uff(z,t)为自由场随着深度方向的竖向位移.
将(1)式中的自由场位移项移到等式右端,等效为加载在杆1上的荷载,变形后的控制方程为
 (2)
(2)
式中: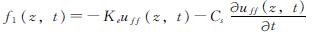 为外加在杆1上的等效荷载.
为外加在杆1上的等效荷载.
将上式进行初始条件为0的拉普拉斯变换,关于时间t的函数可以变换为关于复数参数s的函数,得到下式为
 (3)
(3)
再将式(3)写为状态空间的形式为
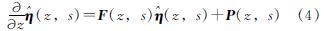
式中的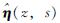 ,P(z,s),F(z,s)可以表示为
,P(z,s),F(z,s)可以表示为

F(z,s)是一个由控制方程中参数组成的4×4矩阵,可以写为
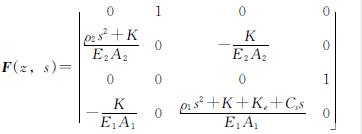 (6)
(6)
根据假设,杆1与杆2顶部为自由端,底部为弹性边界,其边界条件满足以下表达式.
 (7)
(7)
式中kt为弹性边界竖向刚度,c为弹性边界辐射阻尼.
将上述边界条件进行拉普拉斯变换并也写为矩阵的形式为

则矩阵Mb和Nb分别为
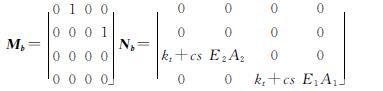 (9)
(9)
根据Liu的分布传递函数法公式[31],在s域内控制方程(3)式的解可以表示为
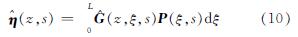
式中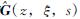 的形式为
的形式为
 (11)
(11)
式中:
Φ(z,ξ,s)为状态转移矩阵,其形式为
Φ(z,ξ,s)=U(z,s)U-1(ξ,s)(13)
式中:
U(z,s)=ezF(s)(14)
杆1上的等效外荷载为 ,在频域中uff(z,t)可以表示为下式.
,在频域中uff(z,t)可以表示为下式.
uff(z,t)=Uff(z)eiwt(15)
式中Uff(z,t)可以进一步表示为[33]
uff(z,t)=cos(ksz)u0eiwt
其中:
式中:u0为土体表面的简谐振动位移幅值; w为圆频率; Gs=Es/2(1+vs)为土层的剪切模量; Es、ρs、βs和vs分别是土层的弹性模量、密度、阻尼比和泊松比.将上式代入到荷载向量P(z,s)中并且把s替换为iw,通过式(10)可以得到系统的解析解向量为
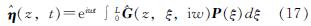
其中P(ξ)表达式为
 (18)
(18)
(6)式中体现场地土层与竖井相互作用的分布弹簧刚度和辐射阻尼系数可以写为[34]
 (19)
(19)
式中:系数a0=wd/Vs,d为竖井外径,Vs=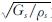 为土层剪切波速,当w≤wc=π×Vs/2L时,Cs=0.
为土层剪切波速,当w≤wc=π×Vs/2L时,Cs=0.
弹性边界的弹簧刚度和辐射阻尼可以表示为[35]

式中:VLa=(3.4)/(π(1-vs))Vs,式中符号含义同上.
通过将土体顶部竖向位移地震动进行快速傅里叶变换,将其分解为一系列频率和复数幅值,代入本文解析解中,计算出地震动每个频率下的系统响应后,再进行快速傅里叶逆变换,将其变为时域解.同时,本文解析解可以同时计算出杆1和杆2任意位置处的竖向位移及其一阶导数值,可以将系统的竖向位移和应变通过向量的形式简易表达,在工程实践中,可以通过简化为文克勒地基杆系统较容易求得竖井初衬和二次衬砌的竖向位移和应变响应.
本文使用大型通用有限元软件ABAQUS验证上述解析解的合理性与可行性.在软件中使用truss单元建模模拟初衬和二次衬砌,采用谐响应分析得出数值模拟结果.
验证工况参数如下:竖井深度L=60 m,初衬和二次衬砌的弹性模量为E1=E2=34.5 GPa,密度为ρ1=ρ2=2 500 kg/m3,泊松比均为0.2,初衬的外径为D=8 m,厚度为t1=0.3 m,二次衬砌的厚度为t2=0.4 m.竖井周围土层密度为ρs=1 800 kg/m3,泊松比为vs=0.2,阻尼比为βs=0.05,弹性模量为Es=160 MPa.切向弹性连接层的刚度取为K=4×107 N/m.在解析解计算中,初衬的等效线密度为ρ1=18 250 kg/m; 二次衬砌的等效线密度为ρ3=22 000 kg/m,初衬的面积为A1=7.3 m2; 二次衬砌的面积为A=8.8 m2.
如图2所示,采用以上参数在ABAQUS中建模分析:分别建立两根长为60 m的杆模拟初衬和二次衬砌,均采用T3D2单元进行模拟计算,各划分为60个单元,初衬和二次衬砌之间采用线性切向弹簧连接,其边界条件均为顶部自由,底部固定.在初衬的每个单元节点上添加弹簧和阻尼,其刚度和阻尼系数使用式(19)进行计算,将位移地震动快速傅里叶变换后的位移复数幅值通过式(16)计算后施加在有限元模型地基分布弹簧远离结构的一端节点上,再将数值模拟结果进行快速傅里叶逆变换为时域解与解析解进行对比.
本文对z=30 m处初衬和二次衬砌的竖向位移和应变响应进行验证,分别绘制其在地震作用下的时程响应曲线,地震波选取El-Centro波,其加速度时程曲线和位移时程曲线如图3所示.
在地震动作用下,z=30 m处初衬和二次衬砌的竖向位移和应变响应曲线对比验证如图4所示.对比本文解析解与数值解可以看出,分析结果较吻合.为了进一步验证解析解的合理性,分别取初衬和二次衬砌的竖向位移和应变最大值进行对比,解析解和有限元模型的对比结果见表1,其中,误差定义为(解析解计算结果/数值解计算结果-1)×100%.结果表明,保留三位小数后位移解析解与数值解的误差为0,吻合程度较高,应变误差在5%以内,误差可以接受,更加验证了本文解析解的合理性.
在以上验证了本文解析解可行性的基础上,从地基弹簧刚度、二次衬砌刚度和竖井外径的角度分别对初衬和二次衬砌顶部位置的竖向地震位移响应进行参数化分析.
图5所示为通过改变土层弹性模量研究地基弹簧刚度对竖井顶部竖向位移响应的影响,分别取土层弹性模量为Es=80 MPa、Es=160 MPa和Es=240 MPa,其分别对应于1倍、2倍和3倍地基弹簧刚度,其余参数与验证工况保持一致.从图中可得出,在竖向地震动作用下,随着地基弹簧刚度的增大,初衬顶部的竖向位移响应在某些时刻会略微增大,二次衬砌响应却会显著减小.原因可能为初衬在软土地层中振动时缓冲作用较大,而二次衬砌在周围初衬振动作用下,仅受底部边界弹簧刚度影响,刚度较大即坚硬地层下顶部位移响应较小.
为了研究二次衬砌刚度对竖井地震响应的影响,本文通过改变二次衬砌的弹性模量进行参数化分析,分别取二次衬砌弹性模量为E2=26.5 GPa、E2=34.5 GPa和E2=39.5 GPa进行计算,其余参数与验证工况保持一致,图6为三种二次衬砌弹性模量下初衬和二次衬砌顶部竖向位移响应.可见在竖向地震动作用下,二次衬砌刚度的变化对竖井顶部竖向位移响应无显著影响,在竖井结构抗震设计中基本可以忽略不计.
图7为从竖井外径影响的角度对初衬和二次衬砌顶部位置竖向位移响应进行参数化分析,保证竖井初衬和二次衬砌的厚度同验证时一致,对竖井外径D=6 m、D=8 m和D=10 m分别进行计算.从图中可以得出,在竖向地震动作用下,随着竖井外径的增大,初衬和二次衬砌顶部竖向位移响应会减小,其中二次衬砌减小更为明显.这是由于竖井外径增大时与底部地层接触面积增大,使得底部边界弹簧刚度增大,引起顶部竖向位移响应会减小.
本文围绕目前缺乏竖井结构抗震研究实际需求,建立了竖向地震作用下场地土层与竖井结构初衬与二次衬砌相互作用力学模型,针对竖井结构初衬和二次衬砌分别推导建立了其在竖向地震作用下的动力响应解析解,并从地基弹簧刚度、二次衬砌刚度和竖井外径的角度分别对初衬和二次衬砌顶部位置的竖向位移地震响应进行参数化分析,结论如下:
(1)基于广义位移法的基本思想,建立了竖向地震作用下竖井初衬和二次衬砌振动控制微分方程,采用分布传递函数法对其位移和应变响应进行了推导,得到了闭式动力响应解析解,通过有限元分析软件验证了其合理性与可行性;
(2)对地基弹簧刚度、二次衬砌刚度和竖井外径这三个不确定性因素进行参数化分析.发现随着地基弹簧刚度的增大,初衬顶部的竖向位移响应在某些时刻会略微增大,二次衬砌响应却会显著减小,在结构设计中应充分关注场地土的弹性模量对竖井结构抗震的影响;
(3)二次衬砌刚度的变化对竖井顶部竖向位移响应无显著影响,在竖井结构抗震设计中基本可以忽略不计;
(4)随着竖井外径的增大,初衬和二次衬砌顶部竖向位移响应均会减小,其中二次衬砌减小更为明显,在竖井结构设计中应重点关注竖井外径对二次衬砌竖向地震响应的影响.
本研究所推导的解析解和参数化分析结论可为竖井抗震设计提供一定参考,并为今后竖井的抗震研究提供理论方法和科学依据.