基金项目:国家自然科学基金项目(51978571); 陕西省杰出青年基金项目(2021JC-41); 陕西省重点研发计划(2022SF-199,2022SF-121)
第一作者:关晓迪(1995—),男,博士研究生,主要从事结构动力学与抗震、减震技术方面的研究. E-mail: 2837867139@qq.com
通信作者:郭宏超(1981—),男,教授,博导,主要从事工程结构抗震、钢结构方面的研究. E-mail: ghc-1209@163.com
(1.西安理工大学 土木建筑工程学院,陕西 西安 710048; 2.中国建筑西北设计研究院有限公司,陕西 西安 710018)
(1.School of Civil Engineering and Architecture, Xi'an University of Technology, Xi'an 710048, China; 2.China Northwest Architecture Design and Research Institute Co., Ltd., Xi'an 710018, China)
steel corridor; genetic algorithm; tuned mass damper; human induced vibration; parameter optimization
DOI: 10.15986/j.1006-7930.2023.02.008
被动控制装置调谐质量阻尼器(tuned mass damper,TMD)在结构减振控制中的应用越来越广泛,除了对于控制高层结构在地震、风等动力作用下的响应,对于大跨度结构在人致激励下产生的振动响应也已被证明有着良好的减振效果[1].结构被动减振设计的关键在于合理地设置减振装置的力学参数和布置方位[2-3],才能达到最为理想和经济的减振效果.1956年,Den Hartog根据定点理论导出了TMD最佳频率比和阻尼比的最优解析公式[4],推导该公式时为了简化计算,假定主结构的阻尼为0; 对于有阻尼主结构,Warburton[5]表明无法继续利用定点理论推导出最佳参数的解析公式,而是利用非线性数学规划的方法进行求解; 薛素铎[6]、李宏男[7]对于阻尼器在结构中的位置进行了分析,表明合理布置阻尼器可显著提高减震控制效率.目前,TMD参数优化多针对于抗震方面,本文针对TMD在结构人致振动控制中的这两类参数,结合遗传算法进行寻优,并将结果进行对比.
优化问题的核心是寻求合理的数学模型,目标函数与约束条件[8],结构被动减振的优化问题可以描述为在一定的约束条件下,充分发挥减振器的性能将结构的振动响应降低到最小值,其一般性的数学模型可以写成如下形式.
minR(x)=[f1(x),f1(c)](1)
kmin<f1(x)<kmax,Lmin<f2(c)<Lmax(2)
式中:f1(x)为减振装置的参数变量; f2(x)为减振装置的位置变量; K、L为相应的约束条件.
对于减振结构来说,其优化问题的目标并不能精确的表示为变量的具体函数,所以在优化过程中并不能依靠变量的导数或梯度信息,这就要求算法能够自适应的在解空间中找到全局最优点.遗传算法作为一种自适应概率搜索方法对于参数的优化问题具有很好的效果,其可以与有限元方法进行结合来分析复杂的结构问题,并不需要对结构进行简化,且对任意形式的目标函数和约束都可以处理,具有较强的鲁棒性[9].
遗传算法原理为模拟生物界的选择、遗传特点以及优胜劣汰法则,对数个个体(待优化参数)进行编码来组成初始群体,按照个体对环境的适应程度(减振效果)施加选择、交叉、变异等操作产生新的种群,如此循环,从而实现参数的寻优.
{0,1}形式的二进制编码作为遗传算法的基本编码方式,便于个体间的交叉、变异等操作,简单易行,应用最为广泛.
本次参数优化的过程包括了结构人致振动的动力时程分析和遗传算法参数寻优,这里采用Matlab编制算法主程序,通过调用有限元程序进行参数验证,并依据算法自动修改模型参数,循环计算.流程如图1所示.
某站站房改造项目中的一幢办公及商业配楼[10],由于规划条件限制,其建筑角部坐落在一条地裂缝上,按照有关规程的要求对地裂缝进行有效避让后,结构被分为了3个单体结构,为了保证建筑功能的连续性,使用钢连廊的形式将结构连接起来,如图2~3所示.连廊跨度纵向45 m,横向9.5 m,为钢桁架结构形式,在结构高度方向上共设置一个单层桁架和一个双层桁架[11],其中双层桁架设置标高为14~22 m,单层桁架设置标高为5~10 m,第一阶竖向自振频率较低为2.5 Hz,与人正常行走步频接近,容易产生共振导致过大的振动加速度,影响结构的使用功能,为了抑制振动加速度,采用调谐质量阻尼器(TMD)对其进行减振控制.利用Abaqus建立有限元模型如图4,结构杆件采用B31梁单元,楼板采用S4R单元,在钢梁下部设置节点,施加点质量,用具有刚度、阻尼属性的Spring单元将节点和钢梁进行连接来模拟TMD减振装置.
工程设计中TMD刚度、阻尼值常采用Den hartog提出的定点理论最优化参数进行计算,根据双自由度体系的动力平衡方程推导出式(3~4),该公式假定主结构的阻尼值为0,但实际结构中多少均存在一定的阻尼值,这就导致由公式计算出的最优参数与实际的最优参数存在一定误差,为了获得最佳的减振效果,采用遗传算法对这两个力学参数进行寻优.
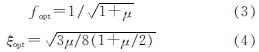
式中:fopt为结构圆频率与激振力频率之比; μ为固定质量比; ξopt为阻尼比.
在进行优化时,采用固定质量比,也就是TMD的质量为常量取4 000 kg,刚度和阻尼系数为变量,为了提高算法的寻优速度,同时排除一些不合理的值,需要指定一个合适的参数取值范围,通常来说结构的阻尼比较小,约为2%~5%之间,最优参数值与利用Den Hartog计算出的参数值相差并不会太大,因此给出待优化参数的取值范围如表1所示.
初始种群为一定数量的个体,每个个体均包含有刚度和阻尼两条染色体,种群越大,越容易找到全局最优解,但消耗的计算时间也越长.本次初始种群数量取为30,采用二进制的编码方式,以原结构和减振结构在共振频率2.5 Hz的人行荷载激励下,跨中节点加速度响应降低的幅度为基础,定义减振率为适应度函数,如式(5).
F(x)=(amin-amax)/amax(5)
式中:F(x)为适应度函数; amax为减振结构加速度响应峰值; amax为原结构加速度响应峰值.
交叉和变异可以使得遗传算法的搜索能力得到提高,同时也是获得新的优良个体的重要手段,采用单点交叉的方法,将种群中任意两个体的染色体编码中任意一位根据交叉概率进行互换,根据变异概率将染色体中的任一位编码进行0~1互换,如图5所示,以此进行交叉、变异操作,达到产生新个体的目的.
选择操作建立在种群中个体适应度评估的基础上,将每代个体按适应度(减振率)大小进行排序,采用末尾淘汰制,每代淘汰适应度排名后5%的个体,用适应度最好的染色体进行代替.
当计算出的适应度在解空间中无对应可行解时,即根据个体约束的取值范围重新随机生成一个个体,相比于罚函数法,使用更加简单.
优化结果过程中适应度随迭代次数变化的曲线如图6所示,可以看出,该算法具有良好的收敛性,当计算到第11代和第17代时,种群中的最大适应度和平均适应度分别达到最大值,说明寻优过程已经结束,提取结果如表2所示,从表中可以看出,遗传算法得到的最优刚度为976 kN/m、阻尼为7.66 kN·s/m,而DH算法计算的最优刚度为966 kN/m、阻尼为7.53 kN·s/m,存在1%~2%的误差.
为了验证优化结果的正确性,计算结构在共振频率2.5 Hz的人行荷载激励下,两种TMD参数时跨中节点的加速度,提取加速度时程曲线[12]如图7所示,可以看出DH算法下的减振结构的加速度响应峰值为0.087 m/s2,非减振结构加速度响应峰值为0.463 m/s2,减振率为81.2%,遗传算法得到的峰值为0.076 m/s2,减振率为83.9%,减振率相比提高了2.7%.
在结构所受激励荷载频率分布较广或主结构自振频率存在偏移时,由多个不同频率TMD组成的MTMD可以扩大减振频带的覆盖范围,相比TMD能获得更好的有效性和鲁棒性[13].当TMD数量较少时,其布置方位可以通过试算来确定,但当TMD数量较多时,位置组合可能多达百种,这时试算已经变得不可能了,通常采用均匀分布的布置方式,但不一定能获得最佳的减振效果,针对这个问题,需要采用遗传算法来对MTMD的位置组合进行优化.
进行优化时,MTMD系统的总质量取为4 000 kg,采用频率呈线性分布的MTMD参数计算方法[14-15],即每个TMD刚度、阻尼相同,质量不同,设置减振频带宽度为2.2~2.8 Hz,个数取为9个,各参数取值如表3所示,通过算法来寻找最优的布置位置.选取各钢梁中点为待选位置,为了减少算法循环优化的工作量且减振器越靠近跨中区域的减振效果越好,设定连廊MTMD的待选位置区域如图8所示,分为上下弦两层,每层17个,共34个待选位置,括号中的数字为下层对应位置编号.
种群数量取为30,种群中的个体为TMD待选位置,每个个体由34个待选位置中随机选出的9个组成,分别对应着m1~m9不同质量的TMD,采用自然数的编码形式,如图9所示.
MTMD系统对减振频段范围内的激励频率均具有减振效果[16],为了评估个体的适应度,定义适应度函数为减振系统在减振区间2.2~2.8 Hz内的总减振率,如式(6).
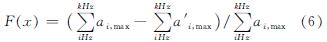
式中:F(x)为适应度函数; a'i,max为减振结构在受到频率为iHz外激励时的加速度峰值; ai,max为原结构在受到频率为iHz外激励时的加速度峰值.
将个体中某个TMD位置与另一个体进行互换,以此来进行交叉操作,将个体中某个TMD的位置改变为解空间中的其他待选位置,以此来进行变异操作,如图 10所示,采用末尾淘汰制,每代淘汰适应度排名后5%的个体,用适应度最好的染色体进行代替,算法参数取值如表4所示.
外荷载为人群以频率为2.2 Hz~2.8 Hz的行走激励,按照上述设定的参数进行遗传算法的寻优计算,迭代过程中种群的最优适应度和平均适应度如图 11所示,当计算到第15代和第21代时,种群中的最大适应度和平均适应度分别达到最大值,说明寻优过程已经结束,得到的MTMD最优布置方位如图 12所示,将结果与均布位置时的结果进行对比,在受到中心频率2.5 Hz的外激励时,最优位置与采用均布位置的加速度时程曲线对比如图 13所示,在减振器均布位置下的加速度峰值为0.099 m/s2,在最优位置时的加速度峰值为0.086 m/s2,减振率提高了13%,对于整个减振频段2.2~2.8 Hz时的加速度峰值如表5所示,总减振效果提高了2.2%.
表5 两种MTMD布置方位下结构加速度峰值(m/s2)
Tab.5 Structural acceleration peaks under two MTMD layout orientations(m/s2)
从对MTMD位置的优化结果来看,采用遗传算法得到的最优布置位置时,可以获得最佳的减振效果,对于中心频率的减振率提升较大,而对频段内的其他频率点提升效果不明显,主要是因为此连廊结构为单阶竖向振型起主要控制作用,而对于各阶模态较为集中,多个振型起控制作用的复杂结构,MTMD位置将对于减振效果影响显著,采用遗传算法进行位置寻优可大大减少由于过多位置组合造成的巨大计算量.
应用遗传算法在对TMD装置控制结构人致振动响应时的参数进行优化分析,具有良好的效果以及收敛性,同时可以得到如下结论:
(1)遗传算法是一种全局性的搜索方法,可以和有限元法联合仿真优化,在TMD参数优化中具有良好的效果,避免了传统优化方法中求全局最优解的困难;
(2)对于连廊TMD减振结构,采用遗传算法得到的最优刚度、阻尼参数可以达到最大减振率,与Den Hartog推导出的最优参数相比,减振率能提高约2.7%,提升的幅度不大,工程应用时DH计算公式应用简单,也能起到很好的减振效果;
(3)对于连廊MTMD减振结构,各质量块的布置位置对于中心频率处的减振效果影响较大,对于减振频段内其他频率点的影响较小,当结构各阶模态较为密集,需对多模态进行减振控制时,MTMD位置对于减振效果影响显著,相比穷举法,采用遗传算法进行位置寻优的优势更加明显.