基金项目:中国地震局地震科技星火计划(XH23055A); 国家重点研发计划(2019YFC1509401); 中国地震局地震应急青年重点任务(CEAEDEM 202223)
第一作者:陈敬一(1990—),女,博士,工程师,主要从桥梁工程抗震研究. E-mail: Chenbjut@163.com
通信作者:周雨龙(1988—),男,博士,助理研究员,主要桥梁工程抗震研究. E-mail: zhouyuong4554@163.com
(1.中国地震灾害防御中心,北京 100029; 2.交通运输部公路科学研究院 旧桥检测与加固交通行业重点实验室,北京 100088)
(1.China Earthquake Disaster Prevention Center, Beijing 100029, China; 2.Key Laboratory of Old Bridge Inspection and Reinforcement Technology Industry, Research Institute of Highway Ministry of Transport, Beijing 100088, China)
Double-deck bridge; rocking structure with yield energy dissipation dampers; dynamic analytical model; seismic response; damper parameters
DOI: 10.15986/j.1006-7930.2023.02.013
双层高架桥因具备有限区域内的交通分流和扩容功能,近年来在我国桥梁工程建设中逐渐得到重视和应用.然而,实际工程中双层高架桥多采用框架墩结构形式,在地震作用下的结构体系受力复杂.基于延性抗震理念设计的双层桥梁结构,利用桥墩塑性铰耗散地震能量以避免结构倒塌,常导致震后桥墩塑性损伤严重,结构难以修复和使用功能丧失,而由此带来的交通中断会严重阻碍震后应急救援和灾后恢复重建的顺利开展[1-4].
摇摆结构体系作为可恢复功能抗震结构体系之一,在限制结构地震损伤的同时具备自复位能力,有望实现减小震后修复成本并缩短桥梁通行功能的中断时间.自1963年Housner首次提出摇摆结构以来,摇摆设计理念在桥梁工程中得到了不断的发展和完善[5].Mander和Cheng[6-7]提出采用无黏结预应力作为提供恢复力元件的摇摆桥墩,并给出了预应力摇摆桥墩结构的抗震设计方法和力-位移简化计算公式.为提高预应力摇摆桥墩的耗能能力,Palermo等[8]提出采用内置耗能钢筋来提高预应力摇摆桥墩的侧向刚度和抗剪能力,随后,学者们针对不同类型的内置耗能装置的预应力摇摆桥墩的抗震性能进行了研究[9-10].为改善内置耗能构件的可更换性、提高桥墩的修复速度,Marriot等[11]提出采用外部可拆卸的耗能构件替代内部配置耗能钢筋的摇摆桥墩,国内学者郭佳等[12]、孙治国等[13]和周雨龙等[14]分别针对外置耗能装置的无粘结预应力摇摆桥墩的抗震性能和设计方法进行研究.目前,关于摇摆结构与双层桥梁结合的研究较少[15-16],其合理构造形式、抗震设计方法等暂无详实依据,其抗震性能还有待深入研究.
本文基于摇摆理念提出一种如图1(b)所示的屈服消能摇摆双层桥梁结构体系.下层桥墩分别与下层盖梁和承台通过无连接措施形成摇摆界面,在桥墩与承台的摇摆界面外侧设置防屈曲阻尼器,上层结构仍为现浇结构.在摇摆墩柱顶端和底端设置钢套筒包裹,盖梁和承台的摇摆界面上设置钢板,以限制摇摆桥墩塑性损伤,并设置挡块来限制桥墩滑动.在横桥向地震作用下,结构通过下层桥墩的摇摆隔震来减小上层结构的惯性力、耗散地震能量,进而避免上层结构的塑性损伤.本文以屈服消能摇摆双层桥梁结构为研究对象,采用拉格朗日方程和动量矩定理建立了该类摇摆框架墩结构的刚体动力反应分析模型,分析了防屈曲阻尼器失效和阻尼器参数对结构地震反应的影响,以期为采用摇摆理念的双层桥梁结构抗震设计提供参考依据.
根据单层双柱式摇摆桥梁结构的振动台试验研究和理论分析可知,具有足够剪力传递机制和变形限制的摇摆桥墩变形模式可简化成桥墩和主梁的刚体运动[17-18].图1(b)所示的双层框架墩结构,其下层摇摆结构的动力行为可近似简化为如图2所示的平面内刚体运动,将上层框架结构简化为一个弹性单自由度体系.图2所示分析模型的变形模式,当施加一个向左地震动激励,摇摆桥墩将初始向右摇摆,此时桥墩转角θ>0; 当地震动激励反向时,桥墩与承台和盖梁之间发生碰撞,且碰撞后摇摆桥墩向左摇摆,此时桥墩转角θ<0.
图2 屈服消能摇摆双层框架墩结构的变形模式
Fig.2 Deformation mode of double-deck rocking bridge system with additional yielding dampers
根据图2所示的几何关系可知,当下层桥墩摇摆时,下层主梁仅发生平面平动,且其水平位移u1和竖向位移w1可由下层桥墩转角θ表示为
u1=2R[sin(±α)-sin(±α-θ)](1)
w1=2R[cos(±α-θ)-cosα](2)
式中:α顶部符号对应θ>0; α底部符号对应θ<0; R为桥墩对角线长度的一半(桥墩尺寸参数); α为墩高和对角线的夹角(桥墩宽高比).
根据图中摇摆界面变形关系,在桥墩摇摆过程中,防屈曲阻尼器的伸长量Δd可表示为
Δd=4bsinθ/2(3)
根据屈服消能摇摆双层框架墩结构的变形模式,该类摇摆结构的运动方程可由下层桥墩转角θ和上层主梁的水平相对位移u2作为广义坐标来表示,通过式(4)和式(5)所示的Lagrange方程推导出运动方程:
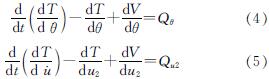
式中:T为体系动能; V为体系势能; Qθ和Qu2分别为对应广义坐标θ和u2的广义力.
双层桥梁结构体系的动能T为
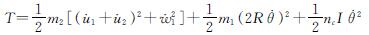 (6)
(6)
式中:m1为下层主梁质量; m2为上层结构质量; I为桥墩绕转动点的转动惯量; I=4mcR2/3; nc为下层桥墩数量.
双层桥梁结构体系的势能V为
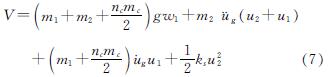
式中:ks为上层墩柱刚度; u··g为水平地震动加速度.
采用Bouc-Wen模型来模拟防屈曲阻尼器的力-位移关系,其屈服力可表示为
Fbd=αbdkbdΔbd+(1-αbd)kbdΔdyzd(8)
式中:kbd为防屈曲阻尼器的弹性刚度; αbd为防屈曲阻尼器屈服后刚度与弹性刚度的比值; Δbd为防屈曲阻尼器的伸长量; Δdy为屈服伸长量; zd为Bouc-Wen模型中无量纲化的滞回参数; zd对时间t的一阶导数为
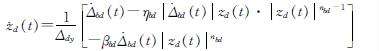 (9)
(9)
式中:αbd、βbd、ηbd和nbd为控制滞回曲线形状的无量纲化参数.
由式(4)得到摇摆双层桥梁结构体系关于下层桥墩转角θ的运动方程为
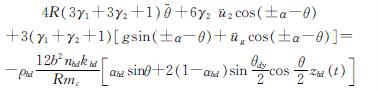 (10)
(10)
式中:γ1为下层主梁与摇摆墩柱质量比,γ1=m1/ncmc; γ1为上层主梁与摇摆墩柱质量比,γ2=m2/ncmc; ρbd为阻尼器刚度系数.
由式(5)中得到摇摆双层桥梁体系关于上层主梁水平位移u2的运动方程为
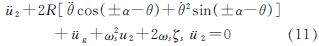
式中:ωs为上层结构固有频率,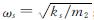 ; ξs为阻尼比,
; ξs为阻尼比,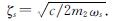
当桥墩摇摆方向发生变化时(即θ变号),摇摆桥墩将分别与盖梁和承台发生碰撞,而式(10)和式(11)所示的运动方程仅适用于θ≠0的情况.根据Housner[5]和Kalliontzis等[19]的研究成果,桥墩角速度折减系数来考虑摇摆结构碰撞前后能量的变化,根据摇摆结构在碰撞前后的动量矩守恒,得出摇摆桥墩的角速度折减系数e为
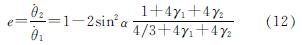
当防屈曲阻尼器伸长量超过限值Δbdu时(即Δbd>Δbdu),防屈曲阻尼器将会被认为失效.根据图2所示的几何关系可知,防屈曲阻尼器失效时所对应的桥墩转角θbdu可表示为
θbdu=2arcsin((Δbdu)/(4Rsinα))(13)
式中,失效伸长量Δbdu与防屈曲阻尼器的构造形式、材料特性和耗能段无黏结长度相关.
以采用常规双层桥梁结构尺寸的摇摆桥梁为研究对象,双层高架桥的上层和下层主梁均为预应力钢筋混凝土箱梁,标准跨径30 m; 桥梁结构采用双层框架桥墩,结构如图1(a)所示,桥墩上、下层墩柱截面不同,上墩柱截面为1.8 m×1.6 m,下墩柱为2.0 m×1.8 m,横梁与墩柱同宽,上、下立柱纵筋配筋率分别为2.46%和2.74%.下层结构质量约为1 000 t,上层结构质量约为1 160 t,下层结构墩柱总质量约为364 t.由此得出模型参数分别为α=0.15、R=6 m、γ=2.745、η=1.16、ωs=20.686 rad/s和ζs=0.05.防屈曲阻尼器的无黏结耗能段长度设定为0.5 m,阻尼器失效时的伸长量Δbdu=0.1 m,阻尼器的其他参数取值为kbd=1 342 kN/m、αbd=0.25、βbd=0.55、ηbd=0.45、nbd=1和ρbd=1.0.
选取远场地震动1992Landers(台站YER360)、近场地震动2002Denali(台站PS10-047)和脉冲近场地震动1999Chi-Chi(台站TCU084-E)的加速度记录作为输入加速度.采用本文建立的刚体动力分析模型计算结构的地震反应,同时列出了未考虑阻尼器断裂情况的结构地震反应作为对比.图3和图4分别为结构的上层墩柱和下层墩柱漂移率时程.由图可见,在远场地震动和近场地震动作用下,考虑阻尼器失效情况和未考虑阻尼器失效的上层墩柱峰值漂移率相差不大; 而考虑阻尼器断裂情况的下层墩柱峰值漂移率大,且结构在近场脉冲地震动作用下发生了倒塌.墩柱峰值漂移率大于阻尼器失效时的墩柱漂移率值会导致结构地震反应相差大,因此,不考虑阻尼器失效可能会低估结构的地震反应,引起强震作用的下结构地震安全问题.
通过前文分析可知,阻尼器失效对屈服消能摇摆结构的地震反应影响较大,因此,合理确定防屈曲阻尼器的设计参数至关重要.采用上节中的模型参数为基准模型参数,针对阻尼器刚度系数ρbd和失效伸长量Δbdu进行地震反应参数分析.为分析不同地震动类别对结构地震反应的影响,本文采用FEMA[20]推荐的50组100条水平地震动记录对结构进行地震反应分析,将其分为22组远场地震动组(FF)、14组无脉冲近场地震动组(NF)和14组脉冲近场地震动组(NFP).将加速度的峰值调整为0.408 g(E2地震水准、III类场地和8度设防烈度).
图5和图6分别为参数ρbd和Δbdu对屈服消能摇摆双层框架墩结构地震反应影响的分析结果.由图5可见,上个层墩柱漂移率随着ρbd的增大呈明显的增加趋势,而下层墩柱峰值漂移率的均值随着ρbd的增大而减小,结构的倒塌次数和阻尼器失效次数随着ρbd的增大而降低,近场脉冲地震动作用下防屈曲阻尼器更易失效.由图6可见,阻尼器失效伸长量的变化对结构近场无脉冲地震反应和远场地震反应的影响不大,下层墩柱近场脉冲地震反应随着Δbdu的增大而减小,而Δbdu>0.12 m之后,下层墩柱漂移率变化不大,这主要由于Δbdu较小时,在地震动作用过程中易失效,结构倒塌工况和阻尼器失效工况数量随着Δbdu的增加有减少的趋势.
图5 屈服消能摇摆结构刚度系数ρbd对峰值漂移率均值的影响
Fig.5 Effect of stiffness coefficient ρbd of rocking system with yielding dampers on average peak drifts
图6 屈服消能摇摆结构失效伸长量Δbdu对峰值漂移率均值的影响
Fig.6 Effect of elongation at failure Δbdu of rocking system with yielding dampers on average peak drifts
以屈服消能摇摆双层桥梁结构为研究对象,采用拉格朗日方程和动量矩定理建立了该类摇摆框架墩结构的刚体动力反应分析模型,分析了防屈曲阻尼器失效和阻尼器参数对结构地震反应的影响,得出以下结论:
(1)基于摇摆刚体假定,采用拉格朗日方程和动量矩定理建立了屈服消能摇摆双层桥梁的动力反应分析模型,该模型考虑了桥墩复位碰撞造成的能量损失和防屈曲阻尼器的失效;
(2)对采用常规双层桥梁结构尺寸的屈服消能摇摆框架墩结构进行地震反应分析得出,不考虑阻尼器失效有可能会高估结构的地震反应,尤其是在脉冲近场地震作用下的情况;
(3)通过对防屈曲阻尼器的参数对结构地震反应的影响分析,得出在合理阻尼器刚度的范围内,刚度越大结构减震效果越好,而阻尼器失效伸长量过小不利于减小结构地震反应.