基金项目:黑龙江省自然科学基金联合引导项目(LH2021E123)
第一作者:刘金龙(1978—),男,博士,副研究员,主要从事地震工程灾害模拟、防灾减灾工程等研究. E-mail: liujinlong@iem.ac.cn
通信作者:陈 晨(1997—),男,硕士生,主要从事结构抗震研究。E-mail: chenchester2019@163.com
(1.中国地震局工程力学研究所 地震工程与工程振动重点实验室,黑龙江 哈尔滨 150080; 2.地震灾害防治应急管理部重点实验室,黑龙江 哈尔滨 150080; 3.上海建工二建集团有限公司,上海 200090)
(1.Key Laboratory of Earthquake Engineering and Engineering Vibration, Institute of Engineering Mechanics, China Earthquake Administration; Herbin 150080, China; 2.Key Laboratory of Earthquake Disaster Mitigation, Ministry of Emergency Management.Herbin 150080, China; 3.Shanghai Construction Engineering Group Co.Ltd., Shanghai 200090, China)
RC frame structure; earthquake; collapse process; ruin; influence range
DOI: 10.15986/j.1006-7930.2023.02.015
钢筋混凝土(RC)框架结构作为最受欢迎的房屋结构类型之一,在世界范围内得到了广泛应用,特别是在新兴的大中城市地区,RC框架结构在房屋中所占的比例非常高.房屋倒塌是地震作用导致的最严重的结构破坏形式,也是造成重大人员伤亡及经济损失的主要诱因.同时,因为道路两侧房屋建筑倒塌会产生大量的废墟,这些废墟往往堆积在道路两侧,对道路通行能力产生较大的影响甚至将其完全堵塞,导致震后应急救援行进路线受阻.汶川地震的实际震害经验表明,对于按照Ⅶ度抗震设防的RC框架结构,当实际烈度低于Ⅸ度时,房屋发生倒塌的概率非常低[1],证明了我国所采用的“三水准、两阶段”的建筑抗震设计方法的有效性,但在实际地震烈度达到Ⅺ度时,框架结构依然不可避免的会出现较大数量的倒塌破坏[2].可见,开展RC框架结构地震倒塌及其影响范围的研究具有重大的研究意义和应用价值.
针对RC框架结构倒塌的研究已经开展了比较多的工作.在早期的研究中,特别是在20世纪80—90年代的研究主要集中在RC框架结构的主要构件以及材料本构关系模型等方面,如Takizawa、Park、Li、Harumi等[3-6]通过编制有限元程序实现RC框架结构主要延性构件的地震损伤发展特征及其数学模型表达方式,为实现框架结构倒塌模拟奠定了基础.而结构实验技术的发展以及大型有限元软件的出现,拓展了RC框架结构倒塌研究的技术方法.Elwood、Galanis、Wu等[4-7]通过振动台试验及大型有限元模拟等方法研究了复杂荷载作用下RC框架结构的倒塌问题,分析了配筋率变化对倒塌发展机理的影响,提出了对钢筋混凝土框架结构极限倒塌临界模型以及位移角的计算方法.
我国学者陆新征、刘海卿、阁东东、阎红霞、祝小凯、刘浩等[10-16]基于MSC.MARC、Ls-dyna、Abaqus等有限元软件,对RC框架结构地震倒塌过程及影响因素进行了讨论分析.另外,顾祥林、张富林、郑瑞杰、周健等[17-20]采用离散单元法,通过建立RC框架结构的离散元模型,对结构地震连续倒塌进行了模拟,并与有限元法进行了比较,验证了离散单元法在连续倒塌模拟中的合理性.同时,叶继红、冯春等[21-22]研究了有限单元法和离散单元法的联合使用问题,分析了耦合交界面、时间步长、以及罚函数刚度矩阵等系列的取值计算问题,对有限元转化为颗粒离散元方面做出了比较深入的研究,并基于有限元与离散元的耦合模型对网壳架构进行了倒塌分析.
综上,可以发现目前在RC混凝土框架结构倒塌分析时,对材料应变率的考虑还很少,而在地震等动力荷载作用下,钢筋混凝土材料以及构件的应力应变关系受应变率的影响也不容小视[23-24].值得注意的是,目前的倒塌研究重要集中于倒塌机理及影响因素的讨论,对于倒塌后废墟的影响范围问题还缺少认识,这对城市灾害路网通行能力等方面的分析具有重要影响.鉴于此,本文通过建立能够考虑应变率影响的钢筋和混凝土材料非线性本构关系模型,建立RC框架结构有限元模型,通过非线性动力时程分析,研究框架结构倒塌过程及其形成废墟的影响范围,旨在为框架结构的倒塌机理及废墟影响范围提供参考.
ABAQUS是一款功能强大的致力于模拟复杂工程问题的有限元软件,因其强大的线性和非线性分析能力得到了设计和科研人员的广泛应用,而Vumat模块则是ABAQUS显式分析中用于定义材料本构关系模型的子程序,通常采用Fortran语言进行编写,本文基于该子程序编制钢筋及混凝土的材料非线性本构关系模型.
鉴于ABAQUS材料库中缺少能够考虑应变率影响的钢筋材料模型,本文引进Johnson-Cook本构模型,该模型于1983年由Johnson和Cook两位学者提出[25],是一种能够考虑大应变和高应变率影响的经验型工程材料本构关系模型,因其模型架构清晰、参数物理意义明确等诸多优点,被很多大型商业软件所采用.
Johnson-Cook材料本构模型的等效应力由以下公式给出[25].
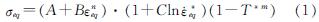
式中:σeq为等效应力; εeq为等效应变; ε·*eq 为等效应变率(无量纲化); T*为温度(无量纲化); A为屈服应力参数; B和n为拟合的硬化系数; C为应变率系数; m为温度系数.
为了实现结构地震倒塌过程模拟,需要考虑材料的损伤失效,引入损伤参数D,同时忽略温度效应的影响.根据黄晓莹等学者[26]的研究,公式(1)转变为

式中,损伤参数D表示每一步等效应变增量和材料断裂应变比值的累积变量,如式(3)所示.

式中:εf为材料的断裂应变,当等效应变达到断裂应变时损伤参数D等于1,表示材料达到断裂失效状态,断裂应变εf可通过式(4)进行计算[26].
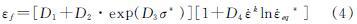
式中:D1,D2,D3,D4为待定的损伤模型参数; k为材料系数.对于需要开发的钢筋材料模型,可通过图1的流程编制程序实现.
与钢筋的本构关系模型相同,因为软件本身缺少能够考虑应变率效应的混凝土本构关系模型,本文采用Holmquist、Johnson和Cook提出的HJC混凝土材料本构模型[27],该模型能够综合考虑大应变、应变率效应、损伤演化效应、围压效应等多种因素的影响,能够较好的描述混凝土材料在地震等动力荷载作用下的力学行为,且因其易于操作、概念清晰等优点得到了诸如LS-DYNA等众多有限元分析程序的引用.HJC混凝土本构模型的屈服面函数可用下式表达.
 (5)
(5)
式中:A、B、N、C、D分别为标准凝聚强度、标准强度增大指数、压力指数、应变率系数以及材料的损伤参数(0≤D≤1); σ*、P*、ε*则分别表示无量纲的等效应力、静水压力以及应变率.
因HJC模型中只考虑了剪切和压缩对混凝土造成的损伤,并未考虑拉伸的影响,根据我国学者徐浩等人提出的动态本构关系对HJC本构模型进行改进[27].通过状态方程确定线弹性阶段、过渡阶段以及压实阶段混凝土静水压力与体积应变的关系; 引入动态增强因子以体现应变率对混凝土本构关系的影响,参考欧洲混凝土委员会以及Gebbekenet等[29]的研究成果确定混凝土拉压强度动态增强因子,将HJC混凝土本构模型的屈服面函数修订如下.
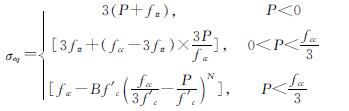 (6)
(6)
式中:B、N为材料参数; ftt和fcc分别为考虑应变率的拉伸强度和压缩强度,按式(7)确定.
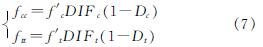
式中:DIFt和DIFc分别为拉伸和压缩强度动态增强因子.对于混凝土材料损伤,拉伸损伤采用基于断裂能的拉伸损伤模型[30],而压缩损伤则可以直接采用HJC模型本身提供的压缩损伤模型,采用相关联的塑性流动势函数,可以推导得到混凝土材料塑性流动因子.
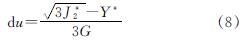
式中:G为塑性流动势函数; *代表按当前增量步的应变和上一增量步的屈服函数和应力值计算的试探应力值.最后,按照图2所示流程Vumat中编制程序,形成混凝土的本构关系模型.
为了验证本文所建立钢筋、混凝土材料本构模型的准确性,结合2011年清华大学的3层钢筋混凝土框架结构倒塌实验的数据[11],对本文所建立模型的准确性进行验证.
图3所示为采用本文材料模型建立的结构模拟结果与实验结果的对比图,从中可以看出,本文编写的材料模型能够较好地反映钢筋混凝土结构在往复荷载作用下的力学性能,特别是在滞回圈形状以及刚度退化、捏缩效应等方面都表现出了不错的效果.与未考虑应变率的本构模型相比,考虑应变率效应的模型在卸载阶段与实验结果的吻合程度更好.但在加载阶段,模拟效果与未考虑应变率的情形相比相差不大.考虑应变率效应后,极限承载能力与实验值更接近.
利用本文第一部分所开发的钢筋和混凝土材料本构关系模型,基于ABAQUS软件建立4层RC框架结构,如图4所示,结构层高3.3 m,平面布置跨度及进深均为6 m,框架柱的截面尺寸400 mm×400 mm,框架梁的截面尺寸为250 mm×500 mm,楼板厚度120 mm.纵筋和箍筋分别采用HRB335、HRB235两种型号,钢筋参数如表1所示,混凝土采用C30,混凝土材料参数见表2.按照普通商业建筑计算横荷载以及活荷载,结构抗震设防烈度为Ⅶ度(0.2 g),按照我国建筑抗震设计规范的要求,采用PKPM软件对框架结构进行配筋设计,框架梁和框架柱的配筋情况见图5.
为了对比不同地震动作用下结构倒塌机理的差异,本文选择了5条不同的地震动进行时程分析,地震动记录的基本信息见表3.通过在结构底部施加速度或者位移时程实现地震动的输入,地震动输入方式采用水平向+竖向耦合输入.采用单元删除法对框架结构进行地震倒塌分析,单元删除法可以解决工程损伤模拟中因材料失效而导致的单元畸变等问题.ABAQUS软件自带的几种损伤模型可以实现单元删除,但对于二次开发的材料模型,需要采用供用户拓展的子程序中的状态变量,通过控制材料积分点实现失效删除,在显式分析学中实现框架结构的倒塌模拟.因本文目标在于上部结构的倒塌及倒塌后废墟分布的研究,暂不考虑土-结构相互作用的影响.
为了考察框架结构的倒塌现象,将5条地震动的峰值地震动加速度(PGA)均调幅至1.0 g并输入结构进行时程分析,同样以汶川地震的卧龙波为例说明结构的倒塌过程.当地震动时间t=8.1 s时,发现结构层间位移角突然发生较大变化,观察此时结构整体破坏情况如图6(a)所示,结构破坏主要发生底部一层和二层,底层跨中的框架柱已经完全毁坏,同时边跨的中柱也发生了严重破坏,框架柱的破坏区域集中在柱子顶端以及梁柱节点区域,大量的混凝土单元已经被删除,钢筋裸露,导致框架柱的竖向承载能力迅速下降,极大的增加了框架梁上所承受的荷载作用,导致梁的跨中发生不同程度的弯曲破坏,此时的梁、柱、节点等局部破坏特征可参见图7.
随着地震动的持续,当t=9.0 s时,底层的大部分框架柱都已经毁坏,少数濒临毁坏,几乎失去了承载能力,在上部荷载的作用下,底层开始发生竖向坍塌,如图6(b)所示; 至t=9.4 s时,底层已经完全坍塌,且随着地震动的持续和竖向坍塌产生的巨大冲击力,二层框架柱几乎在瞬间全部达到毁坏,随之二层结构也发生塌陷,如图6(c),三层甚至也开始发生破坏; 至t=9.6 s时,结构的竖向连续垮塌进一步加剧,在结构底部形成废墟堆积,并且散落在结构周围,如图6(d),对周围的环境造成影响; 至t=9.87 s时,结构倒塌基本结束,所有的框架柱几乎都已经发生了毁坏,完全丧失了承载能力,楼板塌陷,整个框架结构变成一堆废墟,如图6(e)所示.
图6 卧龙地震波作用下框架结构不同时间的破坏状况(PGA=1.0 g)
Fig.6 Failure states of frame structures at discrete times under Wolong seismic wave(PGA=1.0 g)
图7 卧龙地震波作用下框架结构局部破坏特征(PGA=1.0 g,t=8.1 s)
Fig.7 Local failure characteristics of frame structure under Wolong seismic wave(PGA=1.0g,t=8.1
较低烈度下底层柱起始破坏点往往是柱脚部位,而在高烈度下普遍是柱顶发生破坏.分析原因,首先混凝土材料损伤是一个累积的过程,当将柱简化为两端固结杆件时,一般认为底层柱的反弯点在2/3高处,即柱底弯矩一般大于柱顶弯矩,地震烈度较低时,可认为结构相对平稳地进行往复荷载输入,此时柱底的损伤累计高于柱顶.而在高烈度地震中,特别是考虑到竖向地震动作用后,柱顶端以及梁柱节点需要分担楼板产生的惯性力,这时梁柱节点可能因为产生了过高的压应力而破坏.随着中柱柱脚的破坏,中柱的承载能力减弱,角柱所受到的惯性力增大,角柱柱顶发生破坏.
为了实现倒塌及废墟分布模拟,通过模拟刚体的方法来模拟地面约束,建立一个足够大的薄板,并赋予其很大的刚度.同时需要考虑其密度问题,以确保不影响整体结构的稳定时间增量.考虑到结构与地面的摩擦以及地面的不平整等影响因素,在接触中,将结构单元与模拟刚体地面的切向摩擦系数设置为0.65,用于模拟废墟与地面接触后的运动状态[31].
RC框架结构倒塌后,大部分钢筋混凝土的梁柱以及楼板等构件会形成大小不一的碎块彼此粘连的堆积在一起,小部分碎裂的块体会脱离主体结构散落到外围,当然非结构构件以及装饰装修等物体的破坏也会形成大量的废墟,但这部分废墟暂时不在本文讨论,本文只研究主体结构破坏所形成的废墟.倒塌后废墟与地面接触后会由于惯性发生一定的滑动,考虑摩擦以及地面的不平整等影响因素将废墟块体与地面之间的摩擦系数为0.65.如图8所示,图中在建筑物平面周围黑色的部分即为废墟的主要影响范围,为了便于分析,定义一个无量纲的参数:房屋影响范围高度比,即废墟最大影响范围与房屋自身高度的比值,该值反应了房屋倒塌后产生的废墟对周围造成影响的能力,房屋影响范围高度比越大则影响力越大.
表4所示为本文所选5条地震动作用下,框架结构倒塌后废墟的影响范围高度比,从中可以发现,在两个方向上,RC框架结构的影响范围高度比最大值为0.403,也就是说框架结构倒塌后主体结构产生废墟的最大影响范围是房屋高度的0.403倍.另外,通过对5条地震动计算结果的统计,发现在结构短轴方向的影响范围高度比普遍要比在长轴方向大一些,短轴两个方向的均值分别为0.335和0.297,而长轴两个方向的均值分别为0.180和0.157,这也容易理解,在短轴方向房屋刚度比较小,更容易在这个方向发生倒塌,而长轴方向房屋的刚度比较大,发生这个方向倒塌的概率更低些.另外,通过输入地震动水平向与竖向地震动的强度比可以发现,当水平向地震动相同时,竖向地震动分量的强度越高,则房屋倒塌后影响范围高度比越小,说明竖向地震动的强弱对房屋倒塌后废墟的分布具有很重要的影响.
本文以RC框架结构为研究对像,针对ABAQUS软件中材料无法考虑应变率影响的问题,基于Vumat子程序,开发了能够考虑应变率影响的钢筋和混凝土材料本构关系模型,结合清华大学的实验数据对所开发的材料本构模型进行了验证.利用所开发的材料本构关系模型,建立了一个4层RC框架结构,基于单元删除法模拟了框架结构在地震动时程作用下的倒塌全过程,对结构的倒塌机理及其倒塌后的影响范围进行了分析.研究表明:
(1)RC框架结构倒塌破坏往往始于底层轴压比较大的框架柱,特别是中柱率先破坏的概率比较高,而地震动的破坏作用主要体现在柱的中上部位以及梁柱节点处;
(2)竖向地震动对结构倒塌时的侧移及梁、板、柱的破坏状态及倒塌后废墟的分布形态有很大影响.但不同地震作用下,框架结构的倒塌影响范围高度比一般在0.5以内,房屋短轴方向废墟的分布范围相对长轴方向要更广一些,且废墟影响范围的大小与竖向地震动分量的强弱关联性很强;
然而,本文因为未考虑填充墙、装修等非结构构件的影响,对倒塌后废墟的形成机制和体量估计还有一定的偏差,需要下一步工作的继续完善.同时,本文的研究仅仅局限于一个标准的框架结构,计算结果对其他形式框架结构房屋的适用性还有待检验.