第一作者:马振庭(1986—),男,高级工程师,从事建筑结构抗震方面的科研与设计工作. E-mail:317785082@qq.com
(China Railway First Survey and Design Institute Group Co., Ltd.,Xi'an 710043, China)
corrugated steel plate shear wall; seismic behavior; geometric features
DOI: 10.15986/j.1006-7930.2023.02.016
备注
第一作者:马振庭(1986—),男,高级工程师,从事建筑结构抗震方面的科研与设计工作. E-mail:317785082@qq.com
引言
随着现代社会的高速发展,近年来越来越多建筑采用钢结构体系,因其建筑结构具有较高的强度和延性,从而广泛应用于地震灾害地区.
钢板剪力墙在20世纪70年代是一种新型结构,对于抗侧结构在结构抗震性能具有优势,而且在全球多个国家中此结构已经被应用于低层、中高层和高层建筑中.然而近年来,在钢板剪力墙结构中,越来越多的人对使用波纹钢板替代平面钢板产生了关注度.相对于平面钢板,波纹钢板具有多种优点,例如具有更高的耗能能力、刚度、延性和屈曲稳定性.
本文结合前期研究成果,对波纹钢板剪力墙抗震性能研究现状进行系统的分析,为促使该研究的发展提供了帮助.
1 波纹钢板形式改变和组合
在波纹钢板剪力墙应用于建筑结构中,波纹钢板的形式变化是研究人员应该考虑的因素.研究通过对不同的形式的改变,对比在建筑结构中的抗震性能,从而研究出一种更适合建筑结构的形式.
1.1 波纹钢板的几何特征Farzampour等[1]研究了波纹钢板的地震行为,在受单调和循环荷载作用的波纹角度影响下,发现波纹角角度为30°时性能最好,而且随着波纹角度增大会降低刚度和延性,但会增加其极限强度.
Dou等[2]发现影响屈曲荷载的重要因素是波纹重复次数或面板宽度与波纹波长比,其中反映了波纹钢板剪力墙中周围框架对填充板提供的边界约束作用.
Hosseinpour等[3]研究发现了不同波纹钢板几何形状的剪力墙.考虑了不同厚度、深度、长度和波纹密度的波纹梯形板和正弦板,并得出结论,正弦板的刚度和极限强度优于梯形板; 波纹深度的对比,正弦波纹钢板的波纹深度小于梯形波纹钢板的波纹深度; 波纹密度系数则正弦波纹钢板更为有效; 波纹长度的增加导致梯形波纹钢板的厚度减小,但不会改变正弦波纹钢板的刚度.
Fadhil等[4]研究了波纹钢板中波纹角度及其方向的影响,应用横向循环荷载来评估墙体的抗震性能.结果表明,当垂直方向和水平方向的波纹角度分别为30度和20度时,波纹钢板可以达到较高延性.对于水平或垂直方向的波纹钢板,使用10°的波纹角可获得最大强度.
Haris等[5]研究发现梯形波纹板强度、刚度和延性值将随着波纹板厚度的增加而增加,相对于极限荷载增强62%,刚度增强39%,延性增强335%,延性的增强较为显赫.
赵秋红等[6]研究通过在顶梁中部施加低周往复水平荷载的方法,在浅波纹钢板、深波纹钢板和平钢板中进行对比发现,深波纹钢板墙具有更好的性能,结果体现了波纹钢板中的波纹深度对波纹钢板剪力墙的性能影响效果明显.若将波纹钢板的方向进行横向和竖向布置,通过试验发现波纹钢板剪力墙的布置方向对其性能影响不大.
查晓雄等[7]研究了波纹钢板剪力墙弹性抗侧刚度,在波纹钢板与周边框架的边界条件为四边连接,并且波纹钢板剪力墙受力条件为单独受水平荷载或同时受水平荷载和竖向荷载时,钢板波形变化对波纹钢板剪力墙剪切弹性抗侧刚度影响不明显.
波纹钢板剪力墙剪切弹性抗侧刚度由框架抗侧刚度Kf和波纹钢板抗侧刚度Kp两部分叠加组成,即
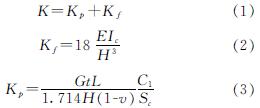
式中:Ic是单根框架柱横截面绕强轴惯性矩; E是框架钢材弹性模量; H是波纹钢板高度; L为波纹钢板宽度; G是钢板剪切模量; t是波纹钢板厚度; ν是钢材泊松比; C1是波纹钢板的一个周期宽度; Sc是波纹钢板一个周期展开后的宽度.
Zhao等[8]研究发现深波纹钢板剪力墙比平钢板剪力墙具有更好的横向刚度、横向强度和能量耗散,而浅波纹钢板剪力墙横向强度低于平钢板剪力墙.因此,建议采用具有深波纹的钢板剪力墙.
钢板剪力墙中墙板的横向强度为
Vn; PW=0.5fytwLcfsin2a (4)
式中:fy为钢材的屈服强度; tw为钢板厚度; Lcf为柱子之间的距离; a为张力场与垂直方向的倾角.
波纹钢板剪力墙深波形钢腹板的侧强度为
Vn; CW=τcrtwLcf (5)
式中:τcr为剪切屈服应力的临界剪切应力; tw钢板的厚度; Lcf柱子之间的距离.
Qiu等[9]研究发现波纹钢板试件不受波纹方向垂直或者水平的影响,但是受较深或较浅凹槽的几何特性影响较大,也体现了波纹钢板具有较高的耗能能力、延性和初始刚度,但是极限强度较低.
Hosseinzadeh等[10]通过对不同角度的梯形波纹钢板剪力墙进行研究,发现随着板波纹角的增大,极限抗剪强度和初始抗剪刚度降低.
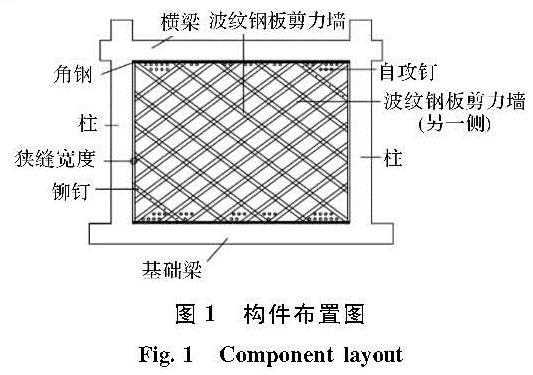
Feng等[11]研究带柱开槽的波纹钢板剪力墙结构如图1所示,发现其具有良好的耗能能力,并且当狭缝宽度在200 mm范围内时,具有较好的耗能性能.
1.2 波纹钢板的力学性能Dou等[12]研究了填充波纹板在纯剪切力作用下的抗剪性能和后屈曲性能,发现受剪波纹钢板对初始几何缺陷非常敏感.
范佳琪[13]研究了钢板厚度、波长、混凝土等级等参数对波纹钢板组合剪力墙的影响发现适当减小剪跨比,有利于增加组合板的抗侧刚度和承载力; 提高钢板厚度,会使组合板的承载力大幅增加; 在设计使用时要注意控制轴压比,不可过大.同时也发现,波纹板的波长、混凝土的强度等级和波纹角度对波纹板的承载力造成较小影响.
王威等[14]研究发现双向加载的试件存在着明显的捏拢效应,而单向加载下没有这样的效应.这种效应使波形钢板剪力墙面内抗震耗能能力的进一步下降,但是随着柱翼缘宽度的增加,这种现象得到了有效的控制.
刚度值是构件抗震性能最重要的参数之一,而刚度退化情况则是反映构件损伤的重要指标,该指标被定义为
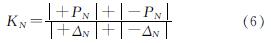
式中:+PN和-PN为第N圈的最大拉力和最大推力; +ΔN和-ΔN为对应的位移荷载值.
谭平等[15]对布置方向进行改变,将横向和竖向波纹钢板剪力墙进行低周往复加载试验研究.发现因为拉力带的展开使竖向波纹钢板剪力墙在延性、屈曲后的承载力和耗能性能方面比横向的波纹钢板剪力墙更具有优势.
赵秋红等[16]研究发现在波纹钢板剪力墙的宽高比的增加和高厚比的降低时,其初始抗侧刚度和极限承载力得到提高; 在波纹钢板波幅的增加时,其极限承载力增大,而初始抗侧刚度的变化较小; 在波纹钢板波长的增加时,对极限承载力和初始抗侧刚度的影响较小.
全剪切屈服和拉力带两种承载方式的理论承载力的计算式为
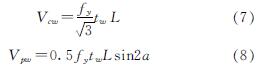
式中:Vcw是波纹钢板抗剪承载力; Vpw是平钢板抗剪承载力; fy是钢板抗拉屈服强度; α为拉力带和竖直方向的夹角; tw钢板的厚度; L为波纹钢板宽度.
Hosseinzadeh等[17]利用有限元方法研究分析了波纹钢剪力墙的线性屈曲,发现减小梯形波纹板的水平侧宽度,只能将屈曲类型从局部改变为整体,但不会增加屈曲强度.
屈曲强度由公式可知
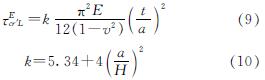
式中:E为杨氏模量; ν为泊松比; a为子面板的宽度; t为波纹面板的厚度; k为根据面板的边界条件和纵横比定义的屈曲系数; H是波纹钢板高度.
Bahrebar等[18]分析梯形钢板剪力墙来评估其性能,通过进行有限元分析,发现适当的边界构件可以显著提高系统的刚度和屈曲.
Cao等[19]通过合理的波纹参数设计,波纹钢板剪力墙能够避免弹性屈曲,且具有较高的初始刚度屈曲、强度、耗能和延性.通过对波纹钢板剪力墙发现板和框相互作用模型能够较好地预测波纹钢板剪力墙的抗剪强度和初始刚度.
波纹板无屈曲时的剪切屈服强度Fwe和波纹板的初始刚度Kwe由下式给出,即

具有刚性梁柱连接波纹钢板剪力墙的极限承载力由下式给出,即
Fu=(τcr+0.5σtysin(2a))Btw+(4×Mf)/(bs)(13)
波纹钢板剪力墙的初始刚度可计算为
K=(GwBtw)/H+(24EIf)/(hs)(14)
式中:B为波纹钢板的宽度; tw为波形剪力墙的厚度; Gw为波纹钢板材料的剪切模量; H是波纹钢板高度; τcr为波纹板的临界剪切屈曲应力; a为钢板中张力场的倾角; bs为相邻柱的中心距; E是波纹钢板的杨氏模量; If为框架的惯性矩; σty为波纹板材料的单轴屈服强度; σy为剪切屈服应力.
Shon等[20]通过波纹钢板剪力墙的框架结构进行研究,发现带波纹板的框架比不带板的框架具有更高的累积能量耗散能力.根据框架中波纹板的布置,失效机制有所不同,首先垂直排列产生局部屈曲,然后是整体屈曲,而水平排列导致整体屈曲.
波纹板的剪切屈曲分别由局部屈曲、整体屈曲和交互屈曲表示.各屈曲强度的方程式如下式.

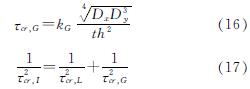
公式中,τcr,L,τcr,G和τcr,i分别为局部屈曲、整体屈曲和交互屈曲的弹性剪切屈曲强度.KL(或G)指局部(或全局)屈曲因子.其长度为正交波纹方向的长度.a是波纹板的最大宽度(取a1与a2的最大值),Dx(或y)是波纹板在强(或弱)轴上的弯曲刚度.t是波纹钢板厚度.
金华建等[21]通过分析不同钢材对波纹钢板剪力墙抗震性能的影响,发现若对于延性要求,波纹钢板剪力墙应选用伸长率大的钢材; 若对于耗能能力要求,波纹钢板剪力墙应优先采用屈服强度低的钢材.
1.3 波纹钢板的不同组合方式陈宗平等[22]研究如图2所示,双波纹钢板混凝土组合剪力墙中的竖向波纹钢板相比横向波纹钢板试件时,竖向波纹钢板的承载力更高,在强度和刚度退化中更为缓慢,而且延性更好,但是耗能较差.若与平钢板进行比较,波纹钢板混凝土组合剪力墙试件的承载力、抗侧刚度、耗能能力均高于平钢板试件.
刘希宇等[23]研究波纹钢板波形和自攻螺钉布置方案对墙体抗剪性能的影响.发现在墙体四周将面板自攻螺钉进行150 mm间距布置时,波纹钢板墙体中肋高为5 mm则具有较好的抗剪性能; 在对螺钉进行加密到75 mm间距布置时,波纹钢板墙体中肋高为15 mm则具有较好的抗剪承载力和初始刚度,但是在峰值过后其强度迅速降低,体现较差的延性.
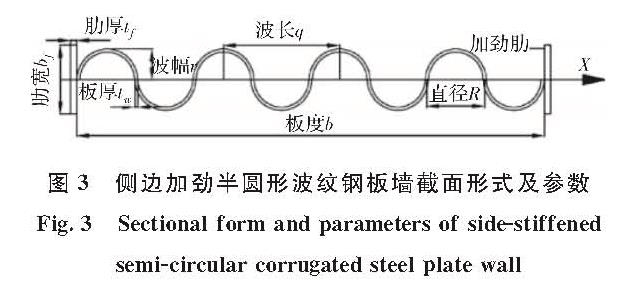
谭平等[24]研究发现随着波纹钢板剪力墙的弹性初始刚度与自复位钢框架第一刚度比及侧边加劲半圆形波纹钢板剪力墙圆弧直径的增大(如图3所示),自复位钢框架-半圆形波纹钢板剪力墙的复位性能降低.但是,当层间位移角大于1%时,耗能能力随着波纹钢板剪力墙的弹性初始刚度与自复位钢框架第一刚度比及圆弧直径的增大而提高.
图3 侧边加劲半圆形波纹钢板墙截面形式及参数
Fig.3 Sectional form and parameters of side-stiffened semi-circular corrugated steel plate wall对于侧边加劲半圆形波纹钢板剪力墙,其弹性初始刚度Kp1为
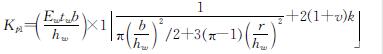 (18)
(18)式中:Ew为波纹钢板剪力墙的弹性模量; hw为板的高度; ν为波纹钢板剪力墙的泊松比; k为剪应力在截面上分布不均的修正系数; b为板的宽度,tw为板厚,r为波幅.
Luo等[25]研究设计了一种新型的波纹板组合剪力墙,通过分析复合剪力墙的破坏过程和破坏模式、滞回曲线、骨架曲线、耗能能力和刚度退化等,可以了解复合剪力墙的抗震性能.相对于钢板剪力墙,波纹板组合剪力墙在滞回性能、能量耗散和刚度退化方面具有极大的改善.
Emami等[26]对于梯形波纹和非加筋钢剪力墙循环性能的实验研究,并对比两者之间的刚度、强度、延性比和耗能能力.发现波纹钢剪力墙和非加劲钢剪力墙均以屈服为主,且随着屈服区扩展,梁与柱连接也相继屈服,并且波纹板试件的总耗能大于未加筋试件.
Tong等[27]通过对双波纹钢板剪力墙进行研究,其由两个梯形波纹板与高强度螺栓连接,利用有限元进行分析,发现可以显著提高其刚度常数.
赵秋红等[28]研究两边连接竖向波纹钢板剪力墙试件的抗震性能(如图4所示).结果发现其具有较好的抗震性能,在抗侧刚度、承载力和延性方面具有优势.在两边连接竖向波纹钢板剪力墙中,其对墙板的布置位置影响较小,并且其初始抗侧刚度和承载力均与墙板宽度具有线性关系,从而设计师可根据建筑内功能和结构性能要求来调整墙板布置.
图4 竖向波纹钢板剪力墙不同墙板位置开洞的模型
Fig.4 Model of opening holes in different wallboard positions of vertical corrugated steel plate shear wall各研究者通过对波纹钢板的形式进行研究,得出结果发现,当加大波纹钢板的厚度可加强波纹钢板的综合性能,尤其在延性方面其增强幅度最大; 波纹钢板的深度对其性能影响较大,发现深波纹钢板更具有优势.深波纹钢板在横向刚度、横向强度和能量耗散方面具有更好的性能; 在波纹钢板中随着波纹角度的增大,极限强度会随着增加,但其延性、极限抗剪强度和初始抗剪刚度会降低; 波纹长度的增加对极限承载力和初始抗侧刚度的影响较小,但会导致梯形波纹钢板的厚度减小,不会改变正弦波纹钢板的刚度; 当波纹钢板波幅的增加,其极限承载力会增大,但初始抗侧刚度的变化较小.
对于波纹钢板的不同组合,运用自攻螺钉或者通过螺栓连接的波纹钢板剪力墙,其不同的布置形式与布置间距会影响波纹钢板的性能; 新型组合的波纹钢板剪力墙在滞回性能、能量耗散和刚度退化下更具有优势; 当两边连接竖向的波纹钢板剪力墙,波纹钢板无论是在中间、左边和右边,其初始抗侧刚度和承载力对于布置位置方式影响较少,所以可根据建筑结构的特定需要进行布置.
2 加劲肋作用于波纹钢板
当建筑结构中单一的波纹钢板对抗震性能不满足的时候,为了使波纹钢板剪力墙具有更好的性能应用于建筑结构中,会采用增加加劲肋的形式.研究人员会探究采用多种形式在波纹钢板中增加加劲肋的方法来使其构件进行加强,探究其不同的抗震性能.
周林丽等[29]研究发现侧边加劲半圆形波纹钢板剪力墙的弹性屈曲临界荷载对比平钢板剪力墙有明显提高,并且随着跨高比的增大、高厚比的减小和半圆形直径的增大,钢板剪力墙的弹性屈曲临界荷载基本呈线性增长,而且侧边加劲肋的肋宽及肋厚对波纹钢板墙弹性屈曲临界荷载的影响较小.
侧边加劲半圆形波纹钢板剪力墙的弹性剪切屈曲临界应力为

弹性剪切屈曲临界应力值即可计算得到弹性剪切屈曲临界荷载Fcr为
Fcr=τcrbtw (21)
式中:E为钢板的弹性模量; a为波浪形波纹钢板的波幅; ks为与边界条件有关的钢板受剪屈曲系数; b为波纹板的宽度; h为板的高度; tw为板厚; r为波幅; v为钢板的泊松比.
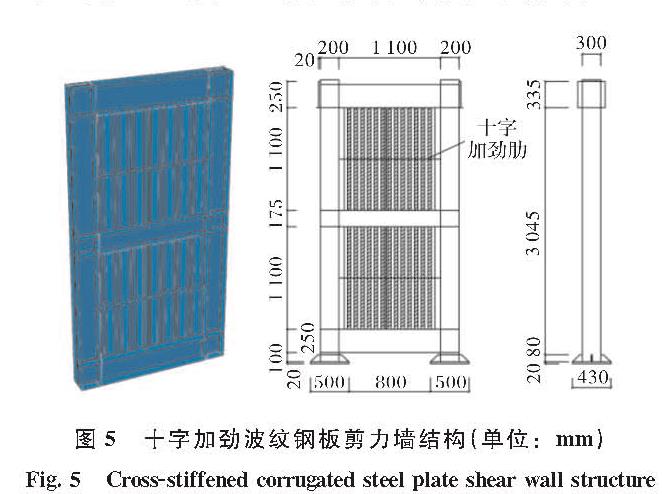
郑宏等[30]在单调荷载作用下和往复荷载作用下对十字加劲波纹钢板剪力墙进行研究(如图5所示).发现波纹钢板的平面外变形分布于板面的上和下两层,对于最大平面外变形具有大幅度的减小,体现了十字加劲肋对波纹钢板对平面外变形具有较好的约束作用,并且对于波纹钢板剪力墙的承载力和刚度退化方面能得到有效的缓解效果.
王嘉政[31]研究发现十字加劲波纹钢板剪力墙中波纹钢板无论是竖向布置还是横向布置,其结构的承载力稳定性均较好,均有良好的延性.当十字加劲波纹钢板剪力墙中的波纹钢板厚度增大时,其结构的刚度、承载力和耗能能力不断增大,但是其结构的延性不断减小.
闫帅[32]研究发现斜加劲肋对波纹钢板面外变形具有较好的限制作用,其提高了试件整体的初始刚度、耗能能力和承载能力.因为斜向加劲肋的作用,所以横向放置的波纹钢板剪力墙与竖向放置时相差不大.
通过对波纹钢板加劲肋的研究,研究者发现,当使用侧边加劲半圆形波纹钢板剪力墙时,其弹性屈曲临界荷载有显著提高,并且加劲肋的肋宽及肋厚对弹性屈曲临界荷载影响较小; 当使用十字加劲波纹钢板剪力墙时,其会提高波纹钢板承载力和有效缓解刚度退化问题.当使用斜加劲肋波纹钢板剪力墙时,其会有效阻止波纹钢板面外变形并提高波纹钢板的整体性能.同时,十字加劲波纹钢板剪力墙和斜加劲肋波纹钢板剪力墙的波纹布置竖向或横向对其影响较小.
3 波纹钢板的开孔形式
随着现代建筑内的布局不断变化,为了方便应用于某种特定需求,往往在建筑结构中可能会对波纹钢板剪力墙进行开洞处理,而设计者则需要考虑开洞后的波纹钢板剪力墙其抗震性能是否满足建筑设计要求.因此,研究人员在对波纹钢板的开孔进行了研究,研究开孔后的构件对抗震性能的影响.
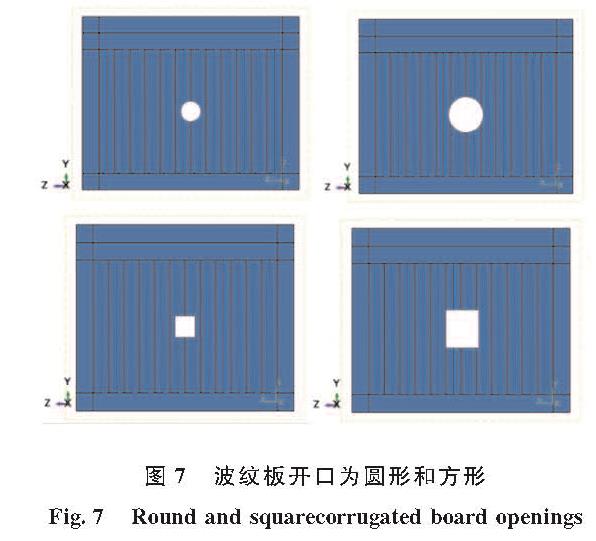
Roudsari等[33]研究开口的几何形状和位置以及板的几何形状和厚度产生的影响(如图6~图7所示).在无开口的波纹钢板中,梯形钢板比正弦钢板承担更多的横向荷载.对于在开口为圆形的梯形波纹钢板的承载能力大于开口为方形的波纹钢板; 开口为方形的正弦波纹钢板的承载能力大于圆形开口; 方形开口的波纹钢板比圆形开口的波纹钢板刚度低.
Bahrebar等人[34]发现腹板穿孔和增加开口尺寸可有效降低初始刚度和弹性极限强度,然而,开口尺寸的变化对结构的延性没有明确和具体的影响.
Farzampour等人[35]对带开口的波形剪力墙进行了永久性研究,比较了开孔和不开孔墙体的效果,并评估了不同的参数,如厚度、波纹角度、开口的位置和尺寸.最后发现采用梯形板可以增加刚度,但会降低极限强度.
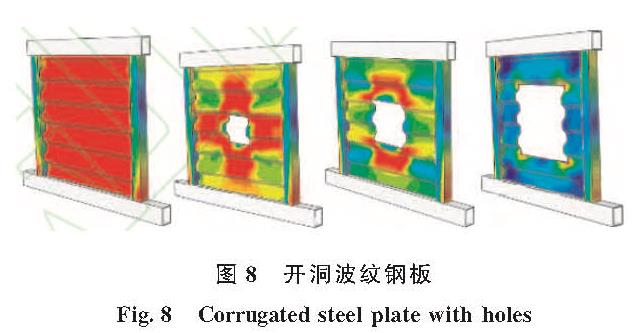
王威等人[36]研究发现当高宽比越小、板厚越大的钢板墙,其受剪承载及耗能性受开洞的削弱作用明显,但对边框柱塑性耗能量削弱程度基本保持一致.当开洞率小于40%时,开洞率越大,承载力和耗能下降越快; 当开洞率大于40%时,波形钢板基本不参加工作,而洞口的高宽比在0.33~0.5之间承载力和耗能性能较好,如图8所示.
Yu等[37]研究发现因无孔波纹板覆盖的剪力墙在循环荷载作用下具有较高的强度和初始刚度,但延性较差.为了提高延性,在波纹墙板中均匀间隔圆孔,改变了剪力墙的破坏模式,提高了剪力墙的延性,但是圆形开孔大大的降低了试件的抗剪强度和初始刚度.
Bahrebar等[38]通过对梯形波纹钢板剪力墙和中心穿孔钢板剪力墙的结构进行性能评估,发现波纹钢板具有较高的承载能力,波纹钢板的几何形状影响其最大承载力.
Bahrebar等[39]研究发现在钢板中心引入孔洞,增大孔洞尺寸,从而降低了钢墙的抗震性能,但是引入适当和足够的钢板穿孔可以减少钢板厚度较大的不利影响.
现代为满足建筑结构设计需求,剪力墙有时需要进行开孔处理,通过对波纹钢板开孔的研究,研究者发现在波纹钢板中的开孔会降低其初始刚度和弹性极限强度,但在波纹钢板中若均匀布置间隔圆孔,则会提高剪力墙延性; 若当适当和足够的波纹钢板穿孔,可以减少钢板厚度较大的不利影响.在同等条件下,波纹钢板剪力墙的承载能力相对于圆形开口和方形开口的波纹钢板剪力墙,圆形开口的波纹钢板剪力墙具有更好的效果.当波纹钢板开洞的情况下,还需要注意波纹钢板的开洞率影响,当开洞率大于40%时,波形钢板的性能就会失效.因此研究发现洞口的高宽比应该控制在0.33~0.5之间,这时的波纹钢板的承载力和耗能性能较好.
4 结语
波纹钢板剪力墙结构体系在多数环境下,其结构性能优于平面钢板,相比而言具有良好的抗震性能.在波纹钢板的几何特征中,其根据波纹不同的厚度、角度和深浅程度体现不同的性能.随着厚度增加延性性能的增强则更为明显; 随着波纹角度的增大其极限强度会增强,但角度为30°时最优; 深波纹钢板更具有较好的抗震性能.根据波纹钢板的力学性能,多数研究者经研究提出多种公式,其中包括刚度退化、屈服强度、初始刚度和承载力等,为后续的研究提供相应的基础理论.波纹钢板与混凝土或钢板的组合形式可提高结构的承载力与耗能性能; 其与螺钉在合理间距中连接可调高抗侧性能; 两边连接的波纹钢板在左、中、右不同位置的布置对结构性能影响不大.
波纹钢板增加加劲肋的方法可约束板面外变形,提高其整体承载力并能缓解刚度退化,从而提高整体抗震性能.波纹钢板中增加开洞尺寸会降低其初始刚度与极限强度,但均匀间隔布置的圆孔可提高剪力墙延性.研究者还需继续对波纹钢板剪力墙进行充分研究,争取可以广泛运用于各种建筑.
5 展望
随着现代建筑的高度越来越高,波纹钢板剪力墙应用于高层建筑将会越来越广泛.需要让其具有较好抗震性能和抵御高层所带来风荷载的影响,充分体现了抗震性能的重要性.
波纹钢板剪力墙在高层建筑中相对于混凝土建筑,其自重较轻且施工方便,可减少建筑材料的使用从而达到绿色环保、节能减排的效果.在采用装配式建造方面,其构件制造统一标准并能加快现场施工速度.为了加快城市化进程并应对可持续发展,建筑工程的绿色节能尤为重要,装配式波纹钢板剪力墙将广泛应用于建筑体系之中.
在今后的研究发展方面,波纹钢板剪力墙应结合减震技术,实现技术减震效果,进而减少建筑物结构体系和建筑物中的设备破坏,从而减少经济损失.其次,现代的建筑内部发展多样性越来越普遍,为了更好的应用于结构的内部建筑设计,未来可以让波纹钢板剪力墙在进行开孔处理的情况下,相应的保持波纹钢板自身的结构性能.同时将来可研究波纹钢板的不同布置形式和框架连接形式,从而提高其抗震性能,进而可更好的应用于建筑结构之中.
- [1] FARZAMPOUR A, MANSOURI I,HU J W.Investigation of seismic behavior of corrugated steel shear walls considering variations of corrugation geometrical characteristics[C]// The 9th Inter-national Symposium on Steel Structures. Korea:2017.
- [2]DOU C,JIANG Z Q,PI Y L, et al.Elastic shear buckling of sinusoidally corrugated steel plate shear wall[J].Engineering Structures, 2016, 121(Aug.15):136-146.
- [3]HOSSEINPOUR E, BAHAROM S, YADOLLAHI Y.Evaluation of steel shear walls behavior with sinusoidal and trapezoidal corrugated plates[J].Advances in Civil Engineering, 2015, 2015.
- [4]FADHIL H, IBRAHIM A,MAHMOOD M.Effect of corrugation angle and direction on the performance of corrugated steel plate shear walls[J].Civil Engineering Journal, 2018,4(11):2667.
- [5]HARIS S.Trapezoidal corrugated plate behavior on Steel Plate Shear Wall[C]//IOP Conference Series: Earth and Environme-ntal Science.IOP Publishing, 2021, 708(1): 012013.
- [6]赵秋红,邱静,李楠,等.梯形波纹钢板剪力墙抗震性能试验研究[J].建筑结构学报,2018,39(S2):112-120.
- [7]查晓雄, 李文韬, 郭明,等.波纹钢板剪力墙弹性抗侧刚度研究[J].哈尔滨工业大学学报, 2021, 53(10):9.
- [8]ZHAO Q, SUN J, LI Y, et al.Cyclic analyses of corrugated steel plate shear walls[J].The Structural Design of Tall and Special Buildings, 2017, 26(16): e1351.
- [9]QIU J, ZHAO Q, YU C, et al.Experimental studies on cyclic behavior of corrugated steel plate shear walls[J].Journal of Structural Engineering, 2018, 144(11): 04018200.
- [10]HOSSEINZADEH L, EMAMI F, MOFID M.Experimental investigation on the behavior of corrugated steel shear wall subjected to the different angle of trapezoidal plate[J].The Structural Design of Tall and Special Buildings, 2017, 26(17): e1390.
- [11]FENG N, WU C.Seismic behavior of nonductile RC frame slotted with corrugated steel plate shear walls[J].Advances in Civil Engineering, 2021,(pt.9):1-23.
- [12]DOU C, PI Y L, GAO W.Shear resistance and post-buckling behavior of corrugated panels in steel plate shear walls[J].Thin-Walled Structures, 2018, 131: 816-826.
- [13]范佳琪.波纹钢板剪力墙结构抗侧性能研究[D].黑龙江:哈尔滨工业大学,2020.
- [14]王威, 罗麒锐, 苏三庆,等.双向加载下波形钢板剪力墙抗震性能研究[J].振动与冲击, 2021, 40(16):8.
- [15]谭平, 魏瑶, 李洋,等.波纹钢板剪力墙抗震性能试验研究[J].土木工程学报, 2018, 51(5):8.
- [16]赵秋红, 李楠, 孙军浩.波纹钢板剪力墙结构的抗侧性能分析[J].天津大学学报:自然科学与工程技术版, 2016,50(S1):152-160.
- [17]HOSSEINZADEH L, MOFID M, AZIMINEJAD A, et al.Elastic interactive buckling strength of corrugated steel shear wall under pure shear force[J].The Structural Design of Tall and Special Buildings, 2017, 26(8): e1357.
- [18]BAHREBAR M, ZIRAKIAN T, HAJSADEGHI M.Nonlinear buckling analysis of steel plate shear walls with trapezoidally-corrugated and perforated infill plates[C]//Proceedings of the Annual Stability Conference, Nashville, Tennessee. USA:Structural Stability Research Council,2015.
- [19]CAO Q, HUANG J.Experimental study and numerical simul-ation of corrugated steel plate shear walls subjected to cyclic loads[J].Thin-Walled Structures, 2018, 127: 306-317.
- [20]SHON S, YOO M, LEE S.An experimental study on the shear hysteresis and energy dissipation of the steel frame with a trapezoidal-corrugated steel plate[J].Materials, 2017, 10(3): 261.
- [21]金华建, 孙飞飞, 李国强.无屈曲波纹钢板墙抗震性能与设计理论[J].建筑结构学报, 2020, 41(5):12.
- [22]陈宗平,周济,莫琳琳,等.双波纹钢板混凝土组合剪力墙抗震性能试验研究[J/OL].建筑结构学报,2021,1-15.[2021-12-12].
- [23]刘希宇,赵岩,李易,等.不同波形的波纹钢板覆面冷弯型钢剪力墙有限元研究[J].建筑钢结构进展,2021,23(7):31-41.
- [24]谭平,周林丽,滕晓飞.自复位钢框架-半圆形波纹钢板剪力墙滞回性能研究[J].建筑结构学报,2021,42(3):185-192.
- [25]LUO Q, WANG W, SUN Z, et al.Seismic performance analysis of corrugated-steel-plate composite shear wall based on corner failure[J].Journal of Constructional Steel Research, 2021, 180: 106606.
- [26]EMAMI F, MOFID M, VAFAI A.Experimental study on cyclic behavior of trapezoidally corrugated steel shear walls[J].Engineering Structures, 2013, 48: 750-762.
- [27]TONG J Z, GUO Y L, ZUO J Q.Elastic buckling and load-resistant behaviors of double-corrugated-plate shear walls under pure in-plane shear loads[J].Thin-Walled Structures, 2018, 130: 593-612.
- [28]赵秋红, 邱静, 郝博超,等.两边连接竖向波纹钢板剪力墙的抗侧性能[J].天津大学学报:自然科学与工程技术版, 2019, 52(A02):8.
- [29]周林丽,谭平,滕晓飞.侧边加劲半圆形波纹钢板墙的抗侧性能[J].西南交通大学学报,2021,5 6(3):550-557.
- [30]郑宏, 王玮, 杨瑞鹏,等.新型十字加劲波纹钢板剪力墙滞回性能探究[J].建筑钢结构进展, 2021, 23(6):8.
- [31]王嘉政.十字加劲波纹钢板剪力墙的滞回性能研究[D].西安:长安大学,2019.
- [32]闫帅.斜加劲波纹钢板剪力墙的滞回性能研究[D].西安:长安大学,2020.
- [33]ROUDSARI S S, SOLEIMANI S M, HAMOUSH S A.Analytical study of the effects of opening characteristics and plate thickness on the performance of sinusoidal and trapezoidal corrugated steel plate shear walls[J].Journal of Constructional Steel Research, 2021, 182: 106660.
- [34]BAHREBAR M, KABIR M Z, HAJSADEGHI M, et al.Structural performance of steel plate shear walls with trapezoidal corrugations and centrally-placed square perforations[J].International Journal of Steel Structures, 2016, 16(3): 845-855.
- [35]FARZAMPOUR A, LAMAN J A, MOFID M.Behavior prediction of corrugated steel plate shear walls with openings[J].Journal of Constructional Steel Research, 2015, 114: 258-268.
- [36]王威,孙壮壮,罗麒锐,等.开洞波形钢板墙受剪承载力及耗能性分析[J/OL].建筑结构学报:2021:1-12.[2021-12-12].
- [37]YU C, YU G.Experimental investigation of cold-formed steel framed shear wall using corrugated steel sheathing with circular holes[J].Journal of Structural Engineering, 2016, 142(12): 04016126.
- [38]BAHREBAR M, KABIR M Z, ZIRAKIAN T, et al.Structural performance assessment of trapezoidally-corrugated and centrally-perforated steel plate shear walls[J].Journal of Constructional Steel Research, 2016, 122: 584-594.
- [39]BAHREBAR M, LIM J B P, CLIFTON G C, et al.Perforated steel plate shear walls with curved corrugated webs under cyclic loading[C]//Structures.Elsevier, 2020, 24: 600-609.