张拉整体结构形态确定过程遵循以下基本假定:各单元连接方式为铰接; 不考虑自重及外部荷载; 不考虑压杆屈曲以及材料非线性; 不考虑结构的局部或整体失稳.

对于一已知n个自由节点、n_f个固定节点、b个单元的张拉整体结构. 根据拓扑连接关系可知其关联矩阵为C^b×n,假定连接单元k两端节点为i和j,则关联矩阵可表述如下.

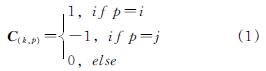
定义Q=diag(q),式中q为构件预应力,根据单元的受力情况可建立平衡方程为

式中:Q为预应力矩阵; X,Y,Z(X_f,Y_f,Z_f)为结构中自有节点(固定节点)在x,y,z方向上的节点坐标矩阵; C_f为固定节点的关联矩阵.

由于张拉整体结构为自平衡结构,节点均为自由节点,因此式(2)可重新描述为:

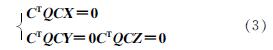
进一步地,上式可表述为

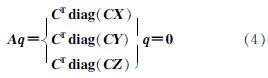
式中:A为平衡矩阵.

结构的自应力模态数s和独立位移模态数m可根据平衡矩阵A求得

s=b-r_A (5)

m=dn-r_A (6)

对平衡矩阵A进行奇异值分解得

A=UVW^T (7)

U=[u₁ u₂ … u_dn] (8)

W=[w₁ w₂ … w_b] (9)

式中:U,W为正交矩阵; V为由矩阵A的非负奇异值组成的对角矩阵. 且此时的自应力模态可分为两种情况^[16]:

(1)自应力模态数等于1

在这种情况下,正交矩阵W可表示为

W=[w₁ w₂ … w_b-1|n₁] (10)

式中:n₁满足线性齐次方程,为预应力系数向量.

(2)自应力模态数大于1

在多自应力模态状态下,正交矩阵可表述为

W=[w₁ w₂ … w_rA|n₁ … n_s] (11)

此时,结构的可行自应力可按向量基的线性组合描述:

q=α₁n₁+α₂n₂+…+α_sn_s (12)

在对平衡矩阵A经奇异值分解得到的多组向量基可通过不同的线性组合,将存在n_s种可行自应力.

此时,通常做法是根据结构的几何外形,人为地将在空间上处于对称位置上的构件归为一组,进行二次奇异值分解以降低解空间的数量. 但随着结构的复杂程度的增加,人为分组极易出错,从而导致无法搜寻可行解.

为解决这个问题,本文提出L2范数分组,无需人为观察结构对称性,直接得到具有可行解的分组方案.

对于对称结构,发现空间上位于对称位置的构件的自应力模态具有相同的L2范数值^[16].

S为平衡矩阵A的自应力模态矩阵,表示如下:

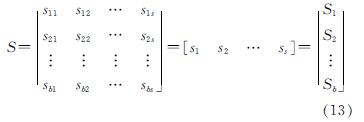
自应力模态矩阵S的每一行可按下式计算为

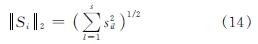
自应力模态矩阵S中每一行代表一根构件,即每一行代表拉索或者压杆,其中具有相同L2范数值的拉索或者压杆被归类为同一组.

使用L2范数得到的分组方案进行二次奇异值分解得到的S^-可分为两种情况:

(1)S^-=1

对于S^-=1,存在唯一解. 该组结果不仅满足结构自平衡,而且满足结构的几何对称约束. 此时在自平衡状态下杆件均满足压杆受压、拉索受拉;

(2)S^- >1

对于S^->1,说明通过分组方案后仍有大于1的解空间,此时需要确定组合系数得到一组可行自应力. 此时建立优化模型,采用智能优化算法求解各组模态相对最优的组合系数,实现整体可行预应力的求解. 最后,对于得到的各组预应力值仍需根据下式进行验证,其中本文误差需满足k≤10^-10.

为保证张拉整体结构在可行自应力状态下的几何稳定,可根据弹性刚度矩阵和几何刚度矩阵得到切线刚度矩阵^[17-18],式(15)中拉索和压杆的ea分别为:e^c_ia^c_i=125 kN/m,e^s_ia^s_i=1 200 kN/m

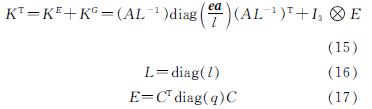
式中,I为单元长度的矢量表达; e为单元杨氏模量的矢量表达; a为单元横截面积的矢量表达; I₃为三维单位矩阵; E为预应力矩阵; 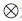为张量积.

若结构稳定,则K^T正定.D所以对于任意一个无穷小位移D,矩阵K^T的二次型是正定的.

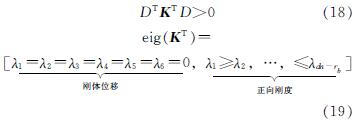
由于K^E和K^G处于非满秩状态,且零空间包含刚体位移,因此需忽略前6个刚体位移情况,通过最小特征值λ₁反映结构的刚度强弱情况.

在张拉整体结构张拉成型时,通常使用结构应变能的变化控制外部张拉设备能量的输入,即

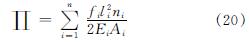
式中:f_i,l_i,n_i,E_i,A_i分别为第i组构件预应力,第i组构件长度,第i组中总构件数,第i组构件的弹性模量,第i组构件的截面面积.

在本文中不涉及截面优化,给定坐标的网架结构的构件长度是定量,预应力可以由式(21)获得

f_k=q_kl_k,(k=1,2,…,b) (21)

从式(20)中可知,决定结构应变能大小的关键参数为预应力大小,故一个合理的初始预应力能够很好地控制张拉成形的施工成本.

综合力密度均匀性要求、拉压关系要求、结构稳定性要求的张拉整体结构预应力优化模型可描述为

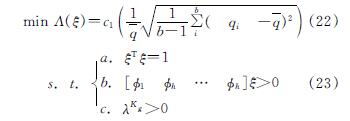
式中:式(22)中Λ(ξ)为力密度均匀度; 式(23)中第约束条件a为自应力模态组合系数的归一化条件; 约束条件b为拉压关系条件; 约束条件c为切线刚度矩阵的正定条件.

天牛须搜索(Beetle Antennae Search-BAS)是由姜向远和李帅等于2017年提出的一种高效的智能优化算法. 和遗传算法、粒子群算法及模拟退火等智能优化算法类似,天牛须搜索不需要知道函数的具体形式,不需要梯度信息,就可以实现高效寻优. 不同的是,天牛须算法是一种单体搜索算法,即天牛须搜索只需要一个个体,使得运算量大大降低.由于其原理简单、参数少、计算效率高,使其在处理低维优化目标时具有非常大的优势.

天牛须搜索算法模仿自然界中天牛觅食行为,在D维空间中天牛的坐标为X=X(x₁,x₂,…,x_n),天牛两只左右触须的坐标被定义为如下公式.

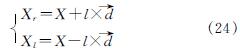
式中:l为天牛质心与触须的距离; 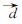为随机单位向量,并对其归一化操作表示为

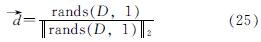
根据左右两根触角感知的气味浓度差进行对比,判断天牛下一步的位置为

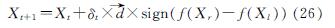
式中:t表示当前的迭代次数; f表示适应度函数; δ_t表示第t次迭代时的探索步长,sign函数为符号函数.

BAS算法存在收敛速度慢、在处理多维复杂问题时,BAS往往会求解失败的问题,使用量子编码(RCQ)及量子旋转门(QRG)增加寻优天牛数量,以增加BAS对多维问题的优化能力.

在量子计算中,量子比特|0〉和|1〉表示微观粒子的两种基本状态,根据叠加原理,量子信息的叠加态可以表示为这两个基本态的线性组合为

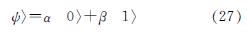
式中:α和β表示量子位状态的概率幅,且满足

α²+β²=1 (28)

|ψ〉表示因观测导致坍缩到|0〉和|1〉态的概率.

量子遗传算法通常采用量子比特的编码方式,而本文采用的是实数编码方式^[19],即引入一个波函数用以表述量子态的坐标和时间,其表示了量子态在相应位置和时间出现的概率为

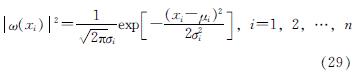
式中:μ为期望; σ为标准差.

α和β两个概率幅值的归一化条件作为约束,一个候选最优解的RCQ可以表示为

每个个体的收敛方向V_J,C被重新表达为

式中:(^overx)_gb是当前全局最优解的观测值.

式中:r_n是产生的一个随机数,x_gb表示式(21)中的期望值,σⁱ_i(|ψ_i〉)表示式(21)中的方差为

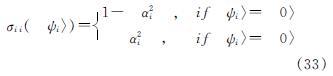
式中:

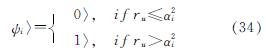
量子比特的进化策略是QRG^[20],作为一种变异算子,将成对的概率幅值更新为适应度最好的一对, 从QRG得到的更新概率幅值按下式计算为

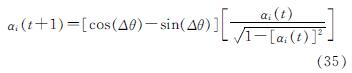
式中:Δθ是旋转角度,相当于定义了当前最佳解的收敛速度步长. 由此可见,实数编码的QRG是一种提高正概率的变异算子.

对于给定的x_gb(t),概率振幅初始化为α_i=β_i=2^1/2/2,i=1,2,…,n. 如果迭代后仍保持当前最优解,则采用QRG增大α,这表示x_gb(t)更有可能是全局最优解. 否则,将概率幅值重置为初始值.

为了防止量子位被困在0或1,采用如下的一个约束限制α_i(t+1)的更新为

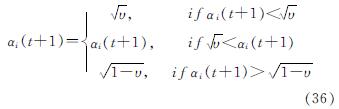
图1给出了量子天牛须搜索算法流程图. 其具体流程如下:

1.设置控制参数和初始化天牛位置;

2.计算初代每只天牛的适应度;

3.赋值当前全局最优解x_gb(t)并且根据式(30)初始化该最优解的量子态;

4.计算每只天牛的收敛方向;

5.如果满足终止条件,则执行最后一步,否则执行第6步;

6.计算第t+1代天牛种群的适应度,获取最优解x_gb(t+1);

7.若x_gb(t+1)=x_gb(t),则进行a操作,否则转至b操作,即

a:通过式(35)进行量子旋转门操作.

b:根据式(36)用量子态初始化t+1代的最优解.

8.输出最优解x_opt=x_gb(t).

图1 量子天牛须搜索算法流程图
Fig.1 Flow chart of beetle antennae search algorithm

该结构采用的是由 单元组成的平面张拉整体梁,具有八个节点、六根压杆、十根拉索. 通过公式(5)确定结构具有三组自应力模态.

根据L2范数值表现出的结构对称性,得到索单元分为3组,杆单元分为2组,如表1所示.

表1 构件的范数值及对应分组
Tab.1 Norm values and corresponding grouping of components

此时采用量子天牛须搜索算法:设置40个天牛个体组成的初始种群,每只天牛搜索的每一步步长长度为1,步长常数c=10,eta=0.95,每次迭代采用式(35)、(36)的量子旋转门进行种群更新,最大迭代次数为150次. 经过如图1的算法流程,可以得到如图3的收敛结果:算法运行3.189 s后目标函数在第35代收敛至最小值.

图3 张拉整体结构梁目标函数的收敛过程
Fig.3 Convergence process of objective function of tensegrity beam

表2给出了通过量子天牛须算法求解的预应力. 结果表明,本文与文献[21]所提出的五组分组方案的结果一致,且结构总应变能更小,在张拉成形时,外力做功更小,经济效益更好,验算误差为k=1.137 6e^-15<10e^-10,满足误差要求.

表2 平面张拉整体结构梁的预应力
Tab.2 Prestress of beam of plane tensioned integral structure

使用图4中曲线的起伏度表示力密度均匀度,显而易见的,使用量子天牛须搜索算法对目标函数优化的效果较文献[21]使用非线性规划法更好.

图4 张拉整体梁的力密度均匀性
Fig.4 Force density uniformity of tensegrity beam

但需要指出是,将力密度均匀性作为目标函数,是为了达到方便施工、节省施工成本为目标. 值得一提的是,文献[21]所使用的分组方法,须进行大量前置工作,即观察结构对称性,得到n种分组方案并筛选出非零解空间的可行方案,这个工作将会非常耗时. 而本文将通过编写计算构件范数值代码就可实现快速自动分组,无需再通过人为观察结构对称性.

在上述初始预应力作用下,可根据式(15)考虑该结构的稳定性,其中切向刚度矩阵特征值满足式(19),说明结构处于稳定状态.

表3 平面张拉整体结构梁切线刚度矩阵特征值
Tab.3 Eigenvalue of tangent stiffness matrix of plane tensegrity structure beam

现有一个由38个节点、40根压杆、93根拉索组成的空间四向张拉整体网架结构,如图5、6所示.

图5 空间四向张拉整体网架俯视图
Fig.5 Top view of spatial four-way tensegrity grid

图6 空间四向张拉整体网架轴测图
Fig.6 Axonometric map of spatial four-direction tensegrity grid

采用范数分组法:根据L2范数值表现出的对称性,将该结构划分为六大模块,在图7中同一类的压杆用数字标记,用不同的颜色用以区分组别:

1.中间的压杆划分为三组连续的压杆,命名为模块a、模块b、模块c.

模块a中第一组连续的压杆,从内向外分为第(1)、(2)、(3)组; 模块b中第二组连续的压杆,从内向外分为第(4)、(5)组; 模块c中第三组连续的压杆,从内向外分为第(6)、(7)组;

2.连接压杆上部端点的索而形成的一个索平面划分为上层索,命名为模块d.

模块d中连续的拉索,从内向外分为第(8)、(9)、(10)、(11)、(12)、(13)组;

3.连接压杆下部端点的索而形成的一个索平面划分为下层索,命名为模块e.

模块e中连续的拉索,从内向外分为第(14)、(15)、(16)、(17)组;

4.而位于网架中部用于拉住上、下两层的竖向索和位于网架四周的用于拉住上、下两层的斜向索,命名为模块f.

模块f中连续的拉索,从内向外分为第(18)、(19)、(20)、(21)、(22)、(23)组.

图7 张拉整体网架拉压构件分组方案
Fig.7 Grouping scheme of tension and compression components of tensegrity grid

经公式(5)可得s=25,采用L2范数分组法快速获得133根构件的分组方案,经公式(14)可得S^-=5,将网架的自应力模态从25降低至5,大大减少了求解变量的维度,再次证明采用L2范数分组方法的便捷性.

采用量子天牛须搜索算法:设置40个天牛个体组成的初始种群,每只天牛搜索的每一步步长长度为1,步长常数c=10,eta=0.95,每次迭代采用式(35)、(36)的量子旋转门进行种群更新,最大迭代次数为150次.经过如图1的算法流程,可以得到对应的收敛过程:算法运行2.508 s后目标函数在第95代收敛至最小值(图8).

图8 四向张拉整体网架目标函数的收敛过程
Fig.8 Convergence process of objective function of four-direction tensegrity grid

从图9可以看出,非线性规划算法有两个明显的尖峰,破坏了整体的力密度均匀性. 结果表明对于复杂的张拉整体网架结构,量子天牛须搜索算法对于目标函数的优化效果大大优于文献[21]所使用的非线性规划法.

图9 张拉整体网架的力密度均匀性
Fig.9 Force density uniformity of tensegrity grid

且结构总应变能更小,在张拉成形时,外部设备输入能量更少,达到方便施工、节省施工成本的目标.

表4 结构构件范数值对应的分组及预应力
Tab.4 Grouping and prestress corresponding to the value of structural member norm

在表4所列的初始预应力作用下,可根据式(15)考虑该结构的稳定性,结果如表5所示,其中切向刚度矩阵特征值满足式(19),说明结构处于稳定状态. 且验算误差为k=1.451 7e¹³<10e^-10,满足误差要求.

表5 四向张拉整体结构网架切线刚度矩阵特征值
Tab.5 Eigenvalues of tangential stiffness matrix of four-direction tensegrity structure