基金项目:黑龙江省科学基金基金(LH2022E123); 中国地震工程与工程振动重点实验室开放专项基金项目(2021D04)
第一作者:刘继兵(1969—),男,学士,高级工程师,主要研究结构抗震设计和加固、工程质量安全监督. E-mail:jibing_liuyl@163.com 通信作者:刘 韬(1993—),男,博士生,主要研究高层建筑结构抗震和结构钢延性断裂. E-mail:tao_liu@tongji.edu.cn
(1.榆林市建筑业综合服务中心(建设工程质量安全监督中心站),陕西 榆林 719000; 2.同济大学 土木工程学院,上海 200092; 3.中国地震局工程力学研究所 地震工程与工程振动重点实验室,黑龙江 哈尔滨 150080)
(1.Yulin Construction Comprehensive Service(Project Quality and safety Supervision Station for Construction), Shaanxi Yulin 719000, China; 2.College of Civil Engineering, Tongji University, Shanghai 200092, China; 3.Key Laboratory of Earthquake Engineering and Engineering Vibration,Institute of Engineering Mechanics, China Earthquake Administration, Harbin 150080, China)
ultra-low-cycle fatigue; replaceable steel coupling beam; coupled wall; multi-scale simulation; coupling ratio; ductile fracture; accumulated plastic energy dissipation
DOI: 10.15986/j.1006-7930.2023.03.009
在现代社会的城市化和可持续发展需求下,高层建筑需具备震后功能可快速恢复(Earthquake Resilience)的能力[1].联肢剪力墙是广泛应用于高层建筑中的结构形式之一.钢筋混凝土联肢剪力墙(RC联肢墙)具有较好的强度和刚度[2].通过控制RC联肢墙的耦合比,可以提升RC联肢墙抗震设计的合理性和经济性[3,4].但是,在汶川和智利震害调查中均发现RC连梁出现严重破坏[5-6],不易修复.将联肢墙的连梁削弱,设置为耗能和变形能力更好的可更换构件,即为带可更换连梁联肢墙,是典型的高层可恢复功能抗震结构体系[7].
可更换连梁形式最早由Fortney 等提出[8],其可分为三段,左右两端为非消能梁段,跨中为消能梁段/可更换构件.消能梁段可采取钢连梁,或在连梁中附加摩擦阻尼器、粘弹性阻尼器、形状记忆合金阻尼器等多种形式[9].而剪切屈服型的钢连梁因其具有较大的刚度和承载力、较好的变形和耗能能力、方便的加工制作等优点作为工程应用的较多的形式[9-13].可更换钢连梁中非消能梁段与消能梁段的连接影响着二者间的有效传力和消能梁段拆卸安装.端板螺栓-抗剪键是目前综合性能较好的连接形式,极限塑性转角可达0.06 rad,更换时间较快,约50 min[14-15].相比传统RC联肢墙,设计合理的带可更换钢连梁联肢墙(RSCB联肢墙)具有较好的抗震性能和震后功能可快速恢复的能力[10,16],墙肢和墙梁节点的损伤程度减小,罕遇地震下层间位移降低,震后的修复成本和时间得到显著提升[11-12,17],其主要原因为塑性变形和耗能集中在可更换钢连梁上,且可较快拆卸安装.
地震作用下,RSCB联肢墙的可更换钢连梁将发生较大的塑性往复变形,破坏形式主要有:翼缘端板焊缝处断裂,加劲肋和翼缘/腹板焊缝处断裂,以及腹板的屈曲和断裂[10-11,13,15].在北岭和神户地震后的震害调查中发现[18-19],预期设计为高延性和高韧性的钢结构也出现多处节点焊缝和母材的断裂.这种在强震作用下钢结构里出现的断裂称为超低周疲劳(ULCF)破坏,即结构钢在循环次数不太多且伴有较大塑性应变下的破坏.因而可更换钢连梁在强震作用下也容易出现ULCF破坏.值得注意的是,震后功能可快速恢复的设计目标是在保证结构地震安全的基础上实现的,所以RSCB联肢墙在设计使用年限内,宜避免可更换钢连梁出现ULCF破坏.而近年来,钢框架梁柱节点和约束屈曲支撑的ULCF性能[20-21]已成为重要研究内容.但是,如前所述,RSCB联肢墙的研究内容主要为体系研究,以及更换钢连梁的形状构造、连接方式和变形耗能等, 对其ULCF性能的研究还尚未成熟.ULCF破坏属于延性断裂,其主要影响因素有等效塑性应变和应力三轴度[22].钢连梁不同位置的等效塑性应变和应力三轴度主要由其累积塑性变形和受到的内力所决定.而在联肢墙中,各层连梁的塑性发展是不同的,位移时程也不同; 且不同位移时程下钢连梁的强化行为也不同,进而又会影响钢连梁受到的内力.故钢连梁的真实位移时程对研究其ULCF性能有重要的影响.但是通过将钢连梁放在联肢墙中进行试验研究的方法所需成本较高,难度较大.
为研究RSCB联肢墙中可更换钢连梁的ULCF性能,首先提出一种多尺度模拟方法,并以联肢墙试验为示例,对试件中的钢连梁进行ULCF性能分析,验证方法的合理性.其次通过该方法对不同耦合比的RSCB联肢墙进行分析,研究耦合比对钢连梁ULCF性能的影响,钢连梁的开裂规律、起裂时间及其预测方式等.研究结果可为分析和预测RSCB联肢墙中可更换钢连梁的ULCF性能提供一种有效方法和参考依据.
研究RSCB联肢墙中可更换钢连梁ULCF性能的多尺度模拟方法技术路线如图1所示.
首先,建立考虑大塑性应变循环加载下的本构特性和ULCF断裂预测的消能梁端/钢连梁精细化模型,并通过该精细化模型标定对应消能梁段简化模型的参数,本文简化模型采用OpenSees平台单元库中的连接单元,该单元在满足精确度前提下,可以实现较高的计算效率; 然后,将标定好的消能梁段简化模型嵌入联肢剪力墙整体模型中,进行数值分析; 其次,根据联肢墙整体的分析结果,选取损伤程度最大的消能梁段,即最不利楼层的消能梁段,或目标楼层的消能梁段; 最后,将目标楼层的消能梁端(简化模型)的位移时程等效施加在精细化模型中.通过模拟结果,对可更换钢连梁消能梁端的ULCF性能进行分析研究和模拟预测.该方法利用多尺度模拟的思路,结合了整体简化模型和局部精细化模型的优势.本章将以联肢墙试验CW-S[23]作为分析示例,对该方法的详细步骤和操作方法进行阐述,并对其合理性进行验证.
首先建立钢连梁的精细化有限元模型,选用通用有限元软件ABAQUS.分析示例CW-S中的钢连梁构造如图2所示,中心腹板处为低屈服点钢,是联肢墙的主要消能区域,其余部分为屈服强度更高、硬度更大的A572钢,其具体尺寸详见文献[23].
在地震作用下,连梁的消能段首先进入屈服,发生大塑性往复变形.故选择合理准确的钢材循环塑性模型是建立消能梁端精细化模型的第一步.首先通过材性试验的结果标定单轴拉伸下材料的本构关系.在试件颈缩之前,材料真实应力应变和工程应力应变的关系见式(1)和(2).
σ=s·(1+e) (1)
ε=ln(1+e) (2)
式中:σ和ε是真实应力和真实应变; s和e是工程应力和工程应变.考虑了颈缩现象缓慢发生的影响, 并对颈缩后的真实应力应变曲线进行修正.图3为模拟结果和试验结果的对比,可以看出模拟结果吻合很好,说明材料的单轴真实应力应变取值合理.
图3 工程应力-应变曲线和断裂模拟结果
Fig.3 Simulation results of engineering stress-strain curves and fracture prediction
可更换钢连梁的消能梁段腹板宜采用Q235或LY225[10],通过试验结果表明,Chaboche混合强化模型可以很好地模拟软钢的循环塑性行为[24].金属材料宜采用Mises屈服函数,Chaboche混合强化模型的屈服函数为
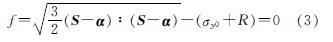
式中:S为偏应力张量; α为背应力张量,本文模型中选取3个背应力张量考虑材料的随动强化行为; σy0是初始屈服应力; R为各项同性强化指数.通用有限元软件ABAQUS已包含Chaboche随动强化模型,只需要输入材料单轴真实应力和应变数据.Chaboche混合强化模型各向同性强化参数可采用文献[24]方法进行标定,在循环试验中,可将材料的后继屈服面写为
σmono=σy0+2R (4)
式中:σmono为后继屈服真实应力,详见图4所示.通过单轴真实应力应变曲线,利用该方法即可得到各项同性强化指数R.
结构钢的ULCF破坏属于延性断裂,其微观机理可分为空穴形核、成长和合并三个阶段[25].通过Rice和Tracey的研究成果[22],空穴的成长主要由应力三轴度T和等效塑性应变εeq所控制,T和εeq的计算公式如下.
T=σm/σeq (5)
σm=1/3(σ1+σ2+σ3) (6)
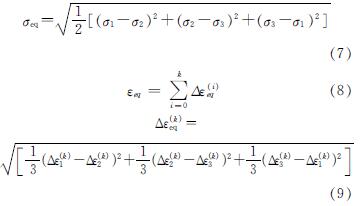
式中,σm和σeq分别是静水压力和Miese等效应力; σ1、σ2和σ3为主应力; Δεeq为等效应变的增量; k为增量步; ε1、ε2和ε3为主应变.在Rice和Tracey的研究基础之上,相关学者提出多种金属延性断裂模型.ULCF模型[20]可以较好地模拟结构钢的ULCF破坏,如式(10)~(12)所示,当断裂损伤系数DULCF达到1时,材料开裂.在循环荷载下,材料的应力受各向同性强化和随动强化所影响,因此也会影响材料的应力三轴度.各向同性强化和随动强化分别是由材料稳定位错和位错堆积引起,而稳定位错对材料损伤影响更明显.故在ULCF模型中考虑了其影响.
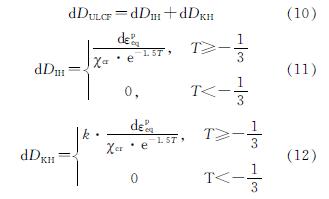
式中,DIH和DKH分别为各向同性强化和随动强化导致的材料损伤系数; χcr为材料的断裂参数,可通过材料的单轴拉伸试验进行标定,本示例中A572钢和低屈服点钢分别取为:1.0和1.3,从图3中试件断裂模拟结果可看出,该参数标定较合理; k为材料常数,取为0.3.ULCF模型可通过ABAQUS的用户自定义子程序USDFLD(用户自定义场变量)进行编写应用.子程序USDFLD允许对单元每个积分点定义,可将断裂损伤系数DULCF通过ULCF模型定义为新的场变量,其函数的自变量需满足材料属性的依赖性,模型中的应力三轴度T和等效塑性应变εeq在子程序中可作为材料属性值的求解数据进行访问,实现自定义场变量DULCF的函数运算,通过DULCF预测材料的断裂损伤行为.
联肢墙数值模型基于OpenSees平台进行分析,见图1,建模方式和单元选取与文献[3]相同.根据钢连梁剪切滞回特性,可采用OpenSees材料库中的Steel02模拟连接单元中的剪切弹簧.Steel02见图5所示,其中屈服应力为钢连梁的屈服剪力Vy,按式(13)计算; E0为连梁的初始侧向刚度K0,按式(14)计算; b为硬化指数,可控制钢连梁二阶刚度; R0、CR1和CR2控制曲线的过渡段; a1~a4控制各向同性强化的参数.
Vy=0.6·fw·Aw (13)
式中:fw和Aw分别为连梁腹板的材料屈服强度和截面面积.
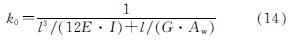
式中:l为连梁长度; E和G分别为材料的弹性模量和剪切模量; I为截面惯性矩.
简化模型的主要作用是将联肢墙目标连梁的实际位移传递给精细化模型.而通过分析,联肢墙在往复塑性变形下,简化模型的二阶刚度是控制连梁往复位移的主要因素,因而在标定简化模型的参数时,只需要一圈大塑性往复加载即可.图6为参数标定后的简化模型与精细化模型的对比.
将标定好的钢连梁简化模型放入联肢墙整体数值模型中,其中墙肢模型的参数选取根据试验获得,详见文献[23].图7给出了试验结果和模拟结果的对照,可以看出模拟整体结果与试验结果吻合较好; 而在加载最后一圈时,底层墙肢出现明显的压溃破坏,故试验结果出现明显的下降.在试验达到屈服位移角0.71%时,试验和模拟结果分别为7 280 kN·m和7 784 kN·m,相对误差为6.9%.通过分析,各层连梁的位移时程影响可忽略不计,满足目标连梁位移的等效传递目标.综上所述,可以说明本文钢连梁简化模型的标定方法和联肢墙整体数值模型是合理的.
根据联肢墙整体数值模型分析结果,选取损伤程度最大连梁的位移时程,并等效施加在连梁精细化模型上.考虑各层连梁均以塑性变形为主要耗能,故可通过各层连梁的累积塑性耗能大小近似判断其损伤程度.图8给出了示例联肢墙中各层连梁随时间的耗能,可知第三层连梁耗能最大,故取其作为目标连梁.将第三层连梁简化模型的位移时程(见图9)等效施加在精细化模型中.
图 10为精细化模型的分析结果,等效塑性应变和断裂损伤系数均集中发展在低屈服点钢的中心区域,符合设计预期.由断裂损伤系数的分布大小可知,腹板中心两侧损伤最严重,该工况下未出现断裂,与试验结果吻合,也进而说明了本文方法的有效性.
选用文献[4]中的联肢墙作为分析算例原型,算例中的钢筋混凝土连梁改为可更换钢连梁,因工字型钢梁因其加工方便、经济性好、可控性强、耐久性优等特点作为工程应用的最多的形式[10],故消能梁段和非消能梁段均为工字截面.采用端板螺栓-抗剪键连接消能梁段和非消能梁段可在二者之间有效传力,便于拆卸安装[14-15],模型不考虑连接面的滑移.分析算例共计2个,分别命名为HCW-1和HCW-2.耦合比是联肢墙设计的重要参数[3,10],2个算例的耦合比不同,且均符合建议设计范围,进而研究不同耦合比下可更换钢连梁的ULCF性能.连梁中可更换的消能梁段设计较为关键,剪切型屈服钢连梁塑性变形能力和耗能能力更好,可通过长度比e/(My/Vy)≤1.6进行控制[10],其中e为消能梁段长度,My和Vy分别为消能梁段塑性受弯承载力和塑性受剪承载力,分别按公式(15)和(13)计算.消能梁段翼缘采用Q345钢,腹板采用Q235钢.为了充分发挥腹板的消能作用,设置加劲肋防止腹板过早出现屈曲,加劲肋采用Q345钢,消能梁段构造如图 11所示.非消能梁段设计为始终保持弹性状态.算例具体信息见表1.
My=fy·Z (15)
式中:fy为材料屈服强度; Z为塑性截面模量.
按照章节一的方法对算例HCW-1和HCW-2的可更换钢连梁进行ULCF多尺度模拟分析.第一步:建立基于ABAQUS的精细化模型,Chaboche混合强化模型和ULCF断裂模型的详细使用方法和参数标定步骤详见第二章节.在该算例连梁中, Q345和Q235钢的断裂参数χcr可分别取为:2.75和2.20[26],考虑焊接对断裂韧性的影响,即热影响区界面更容易发生断裂,焊缝处的断裂参数可取为0.7[20].第二步:根据精细化模型的分析结果,标定基于OpenSees的简化模型参数.由于篇幅有限,前两步的计算结果未列于文中.第三步:对算例HCW-1和HCW-2进行整体模拟分析,整体模型中未考虑钢连梁非消能梁段与消能梁段间的滑移.本文算例采用定幅循环往复加载,水平荷载模式为倒三角分布,采用顶层水平位移控制,加载幅值为0.4%,经过试算,两个算例的循环圈数均设置为20圈.图 12~13为算例中连梁随时间的累积塑性耗能,可以看出,第一层连梁耗能最少,故发生破坏较晚; 在其余楼层中,第五层连梁耗能最多,第二层连梁好耗能较少.对两个算例均选取第二层和第五层的连梁进行ULCF性能分析.第四步:将目标楼层连梁的位移时程等效施加在精细化模型中,进行ULCF性能分析.图 14给出了连梁的滞回曲线,从图中对比可以发现,第五层连梁的位移均大于第二层,故能耗更多.滞回曲线的终点对应连梁开裂点.图 15~16分别为算例HCW-1和HCW-2选取目标连梁的断裂损伤系数DULCF云图,均提取钢连梁起裂点时刻(出现DULCF最大值超过1时)和完成20圈加载后时刻的分析结果,图中的灰色区域代表DULCF大于1的位置,该区域处的红色虚线框的大小也反映了断裂损伤区域的面积.
算例HCW-1和HCW-2在加载过程中,所选第二层和第五层连梁(分别记为CB-2和CB-5)位移时程中的最大值Dmax和最小值Dmin如表2所示,在相同层数下,HCW-2连梁Dmax和Dmin均会更大,说明在联肢墙顶点位移相同的情况下,耦合比较小联肢墙的连梁变形会更大.从图 14也可以看出相同楼层下,整个加载过程中,HCW-2连梁的侧向变形均大于HCW-1连梁的变形.从表2还可看出,相比HCW-1,HCW-2相同楼层连梁的起裂时间也更早,均约为0.9倍,Ncr为起裂时的圈数; 其加载20圈后的断裂损伤系数DULCF_20也更大.从图 15~16的(a)和(c)中可看出,算例连梁的起裂点首先易发生于翼缘焊缝的中心处.在图 15~16的(b)和(d)中,HCW-2的连梁断裂损伤程度更大,范围更广.对于不同楼层,CB-2相比CB-5耗能更小,损伤也较小,说明根据连梁累积塑性耗能的大小选取最不利楼层是合理的.所有算例在加载20圈后,CB-2的断裂损伤均只发生在翼缘焊缝中心处,其损伤程度和范围也较小; 而CB-5的翼缘焊缝中心处的断裂损伤较明显,尤其对于HCW-2,翼缘焊缝外侧的断裂损伤系数可达1.85,在腹板的四个对角处也出现微裂缝.综上所述,在相同顶点位移下,联肢墙耦合比越大,其钢连梁越不易出现ULCF断裂; 本算例钢连梁的断裂部位易先出现在腹板焊缝中心处,其次是腹板四个对角处.
联肢墙各层连梁的变形虽然不同,但是变形模型较相似,即连梁各部分的应力状态较一致.因而在同一联肢墙中,如果各层连梁设计相同,其断裂损伤程度则主要和位移时程有关,也就是说,钢连梁的变形越大,累积塑性应变就越大,则更容易出现断裂.通过以上分析不难发现,对于各层连梁设计相同的联肢墙,累积塑性应变/变形是影响其断裂的主要因素.而连梁的耗能也是通过塑性变形,故可推断,连梁的断裂与其耗能大小成正比.表2给出了HCW-1和HCW-2中CB-2和CB-5的断裂圈数比值(Ncr-CB2/Ncr-CB5)和相同i时刻下CB-2和CB-5的耗能比值(Ei-CB2/Ei-CB5),可以发现,二者几乎相同.此外,表2还给出钢连梁起裂时刻的耗能Ecr,对于所在不同层的相同连梁,Ecr非常接近,HCW-1和HCW-2二者的Ecr分别仅相差1.4%和2.9%.因此,对于各层连梁设计相同的联肢墙,连梁的断裂损伤系数和其累积塑性耗能成正比例关系,故可通过其耗能大小对钢连梁的ULCF性能进行判断和预测.
由上述分析可得,对于每层钢连梁设计相同的联肢墙,在钢连梁Ecr已知的情况下,通过各层连梁之间累积塑性耗能的关系,可快速地从宏观尺度预估每层连梁发生断裂的顺序和时间.究其原因,主要为各层连梁的变形模式一致,均可通过弦转角进行表征,反弯点近似位于连梁中心[27],故各层钢连梁断裂损伤系数的发展也较为一致.而各层连梁不同之处主要为变形的幅值,进而影响了起裂时间.同理,对于钢框架的梁柱节点、耗能钢支撑或金属剪切阻尼器等各层变形模式较一致的构件,可推断在设计相同的情况下,同样能够通过上述方法判断各层目标构件发生断裂的顺序和时间.
研究联肢墙可更换钢连梁ULCF性能的多尺度模拟方法,通过对比分析模拟结果和试验现象,验证方法的合理有效性.具体步骤为:首先建立考虑材料循环塑性和ULCF损伤的合理钢连梁精细化有限元模型; 然后基于OpenSees平台并根据精细化模型的结果建立钢连梁简化模型; 其次对联肢墙进行整体分析,根据连梁累积塑性耗能结果选取目标连梁的位移时程; 最后将目标连梁的位移时程等效施加在精细化模型中,通过断裂损伤系数,分析和预测其ULCF性能,可参见图1.通过该方法分析了不同耦合比的RSCB联肢墙算例,主要结论如下:
(1)联肢墙的耦合比越小,在相同顶点位移下的可更换钢连梁变形和断裂损伤系数越大,起裂时刻也越早.本文算例的塑性耦合比从47%增加至53%,起裂时间约提升了1.1倍;
(2)累积塑性耗能可作为判断其断裂的重要参数,尽管不同楼层的钢连梁位移时程不同,但出现起裂时的累积塑性耗能较为接近.文中两个算例中,不同楼层钢连梁起裂时耗能Ecr分别仅相差1.4%和2.9%;
(3)各层钢连梁设计相同时,连梁间起裂圈数的比值与耗能比值相同.通过各层连梁之间累积塑性耗能的关系,可预估每层连梁发生断裂的顺序和时间.