(1.陕西华山路桥集团有限公司，陕西 西安 710016; 2.陕西正诚工程研究院有限公司，陕西 西安 710016; 3.西安建筑科技大学 土木工程学院，陕西 西安 710055; 4.陕西省岩土与地下空间工程重点实验室，陕西 西安 710055)
(1.Shaanxi Huashan Road and Bridge Group Co., Ltd., Xi'an 710016, China; 2.Shaanxi Zhengcheng Engineering Research Institute Co., Ltd., Xi'an 710016, China; 3.College of Civil Engineering, Xi'an Univ. of Arch. & Tech., Xi'an 710055, China; 4.Shaanxi Key Laboratory of Geotechnical and Underground Space Engineering, Xi'an 710055, China)
horizontal directional drilling; mud pressure; seepage; strength criteria; cylindrical cavity expansion
DOI: 10.15986/j.1006-7930.2023.04.019
水平定向钻是一种按设计轨迹钻进一个小直径导向孔,再进行多级扩孔直至达到设计所需孔径,最后回拖铺管的非开挖施工技术[1-2].在水平定向钻施工中,泥浆起到携带岩屑、冷却钻头、减小摩阻等作用,一定的泥浆压力能够保持孔壁的稳定,而不当的泥浆压力会引发工程问题[3].当泥浆压力过大时,会导致原有路面起拱隆起、出现裂缝、冒浆等; 当泥浆压力过小时,会导致地面沉降过大,孔洞缩径甚至塌孔,严重影响施工效率[4-5].因此,有必要控制合适的泥浆压力,避免孔壁失稳.
为维持孔壁的稳定,一些学者从不同的角度对泥浆压力控制进行了研究分析.Duyvestyn等[6]利用FLAC软件模拟土体塑性变形过程,分析了不同泥浆压力的影响,提出应严格控制泥浆压力.Kennedy等[7]基于圆孔扩张理论,得出了孔壁发生拉伸失效时的极限泥浆压力.Xia[8]通过试验研究了维持孔壁稳定的最大泥浆压力.李斌等[9]通过对孔壁进行弹塑性力学分析, 提出了最优泥浆压力的概念.闰相祯等[10]根据穿越过程中泥浆作用机理、泥浆性能以及地层影响,给出了最小需要泥浆压力和最大允许泥浆压力的计算方法.遆仲森[11]、田恒星等[12]考虑钻井液和地应力共同作用下,孔周应力重分布导致土体破坏来探讨泥浆压力的合理范围.Yan等[13]通过分析比较现场实测的泥浆压力数据与数学模型预测的泥浆压力数据找出一种最优模型来预测最大泥浆压力.Yan等[14]总结了基于不同地层压裂机理对钻孔内最大允许泥浆压力的预测方法.可以看出,学者们通过理论、实验和数值方法对泥浆压力控制问题进行了广泛的研究,但在理论层面,并未直接考虑泥浆浆液渗流的影响.当浆液入渗到土体的孔隙中,会改变土体原有性质; 渗流时产生的渗流体积力和施加的荷载力共同作用于土体,引起土体的应力重分布,进而影响土体的位移和变形[15].曾聪等[16]利用实验研究泥浆渗入土体引起的土体强度参数的改变,从而研究了扩孔过程中泥浆渗入孔壁对塑性半径的影响.付彬等[17]借助有限元程序,通过强度折减系数法表征渗流作用,研究了水平定向钻孔壁稳定性问题.程远泽[18]考虑渗流作用会引起土体软化,引入土体软化系数,推导最大泥浆压力计算公式.可以看出,目前有关水平定向钻泥浆压力的研究中针对泥浆渗流考虑的较少,且都是从土体性能的改变去考虑,而从理论角度考虑渗流体积力影响的研究仍存在不足,且并未考虑强度准则效应,而已有研究已表明,岩土材料的屈服、强度准则对其强度分析有较大的影响[19].
目前,圆孔扩张理论已广泛应用于岩土工程中,定向钻扩孔可简化为无限空间土体中的柱孔扩张问题[20].因此,本文基于柱孔扩张理论,同时考虑浆液渗流和强度准则的影响,对定向钻扩孔问题进行分析; 通过推导柱孔扩张问题的弹塑性解答,得出孔壁周围土体的应力场、位移场和极限泥浆压力的理论计算公式,再由此分析压力控制问题.并以某工程进行算例分析,探究渗流、强度准则等不同参数对泥浆压力控制的影响.为水平定向钻实际施工中的泥浆压力控制提供参考依据.
定向钻的多级扩孔问题可简化为无限空间土体中的柱孔扩张问题,如图1所示.小孔的初始半径r0为设计扩孔半径,孔壁外存在各向同性的初始应力P0,在孔内均匀分布的泥浆压力P的作用下,小孔半径由初始半径r0变为扩孔半径r1.当泥浆压力P达到一定值时,孔周土体开始屈服,出现塑性区,随着泥浆压力逐渐增加, 渗流力随之增加,塑性区不断扩大,在孔壁周围形成环状的塑性区,塑性区以外的土体仍为弹性状态.泥浆压力继续增加,直至增加到极限泥浆压力Pu.以rP表示塑性区半径,则塑性区范围r1≤r≤rP,弹性区范围r≥rP,以urp表示弹塑性交界面位移.规定求解过程中的应力、应变以压为正,拉为负.
图1 孔壁力学模型
Fig.1 Mechanical model of hole wall
针对本文研究内容,作出以下假定:
(1)假定土体为各向同性的理想弹塑性材料;
(2)采用平面应变条件下常用的8种岩土强度准则的统一线性方程作为土体的屈服准则[21];
(3)弹、塑性区土体符合小变形假定;
(4)假定浆液渗流方向以径向为主,且土体孔隙率和孔隙结构变化微小,认为土体渗透系数不变.
张常光[21]归纳建立了平面应变条件下常用的8种岩土强度准则的统一线性方程,本文采用该统一线性方程作为土体塑性屈服的准则,在文中称之为平面应变条件下一般屈服准则,则在柱孔扩张问题中,平面应变条件下一般屈服准则为
σr=Aσθ+B (1)
式中:A、B为关于材料本身c(黏聚力)、φ(内摩擦角)值的参数,不同的参数A、B对应不同的屈服准则.
不同强度准则对中主应力考虑的程度不同,对土体材料强度的估计程度不同,因此,利用不同屈服准则研究泥浆压力控制问题时,所得到的结果会有所差异.为研究不同强度准则对泥浆压力控制的差异影响,选取以下三个在中主应力效应考虑程度上差异较大的准则进行分析.
对于广义的空间滑动面(SMP)准则,即G-SMP准则有
式中:σ0为黏结应力,σ0=ctanφ; F为关于土体内摩擦角φ的参数,F=8tan2φ+9.
对于Mohr-Coulomb 准则(M-C准则)有
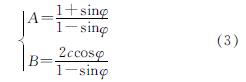
对于统一强度准则(UST),取统一强度理论参数b=1时,即UST1准则有
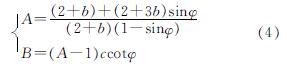
在孔内的泥浆浆液挤压土体的过程中,由于压力差的存在,泥浆会向土体内部发生渗流,泥浆在土体孔隙中流动,产生渗流体积力,其运动状态符合达西定律.柱孔扩张问题中浆液渗流为轴对称分布状态,由渗流基本原理通过转换可得到定向钻扩孔问题下渗流体积力的基本微分方程为[22]为
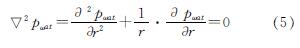
式中:Pωat为渗流体积力.
考虑到塑性区的发展对孔周土体稳定性的影响最为显著[23],本文仅考虑渗流体积力作用在塑性区内,则渗流边界条件为
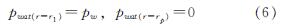
式中:Pw为泥浆渗透压力.
联立式(5)、式(6)可得渗流体积力为
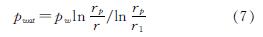
考虑渗流影响下的平衡微分方程为
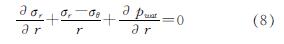
式中:σr为径向应力; σθ为环向应力.
几何方程为
式中:εr为径向应变; εθ为环向应变; ur为半径r处的径向位移.
弹性区物理方程为
式中:E为土体弹性模量; v为泊松比.
当泥浆压力大于临塑压力,孔周土体处于弹塑性状态,此时,塑性区外围弹性区的应力边界条件为
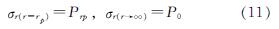
式中:Prp为弹塑性交界面处应力.
联立平衡方程式(8)、几何方程式(9)、物理方程式(10)、弹性区边界条件(11),可得弹性区任一点的位移为
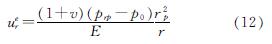
弹性区任一点的应力为
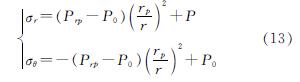
在弹塑性交界面(r=rp)处,σr、σθ满足式(13),则在r=rp处有
塑性区径向应力和环向应力满足屈服准则式(1),将式(14)和式(1)联立得弹塑性交界处应力
塑性区应力边界条件:
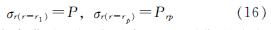
塑性区应力满足屈服准则式(1)、平衡微分方程式(8)和边界条件式(16),将式(1)代入式(8)解得
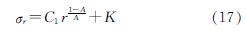
式中:K=Apw/[(A-1)ln(rp/r1)]-B/(A-1),为与渗流、土体c、φ值有关的参数; C1为积分常数.
积分常数C1可将式(16)代入式(17)得到:
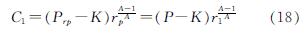
联立式(15)、式(17)、式(18)可得塑性区任一点的应力为
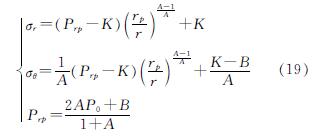
塑性区弹性应变满足胡克定律,联立式(10)、式(19)得塑性区弹性应变为
式中:εer、εeθ分别为塑性区弹性径向应变、弹性环向应变.
由于岩土体摩擦型材料的特点,选取非相关联流动法则能更好地符合这一特性[24].在塑性区选用非相关联流动法则[25],平面应变条件下径向塑性应变εpr和环向塑性应变εpθ的关系可以表示为[26]
式中:m为土体剪胀参数,m=(1+sinψ)/(1-sinψ); ψ为土体剪胀角.
联立式(9)、式(20)、式(21)解得关于塑性区位移upr的微分方程通解为
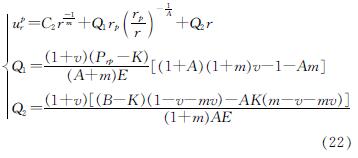
式中:C2为积分常数; Q1、Q2为与剪胀、渗流、土体弹性模量、泊松比有关的参数.
将式(16)代入式(22)解得
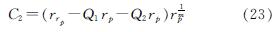
弹塑性交界面(r=rp)处的位移urp满足式(12),将r=rp代入式(12)得
式中:Q3为关于材料弹性模量、泊松比、初始应力的参数.
将式(24)和式(22)、式(23)联立可得塑性区任一点的位移为
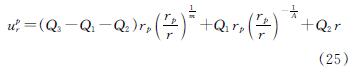
由于土中存在各向同性的初始应力,在初始应力下产生的初始位移为
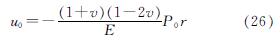
则在泥浆压力下,塑性区径向位移(相对位移)表达式为
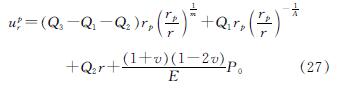
在浆液扩孔过程中,浆液与土体交界面的移动距离即为扩孔半径r1处的位移[27],即
对式(18)作变换可得塑性区半径rp、扩孔半径r1、泥浆压力P之间的关系为
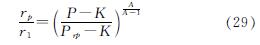
结合式(28)、式(29)可以得到关于初始孔半径、扩孔半径和泥浆压力三者的关系式,而当扩张后孔半径r1相对初始孔半径r0无限大,即r0/r1→0,可得泥浆压力极限值Pu的表达式为
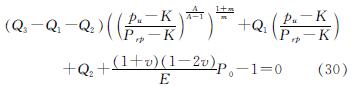
当土体参数已知时,即可利用式(30)求得极限泥浆压力.
为验证理论的适用性,并进一步说明考虑渗流的必要性,基于本文理论分别计算考虑渗流和不考虑渗流情况下的极限泥浆压力值,并与试验实测结果[28]进行对比分析,如图2所示.
图2 极限泥浆压力计算值与实测值的对比
Fig.2 Comparison between calculated and measured values of limit mud pressure
可以看出考虑和不考虑渗流的理论计算值均高于实测值,这种差异可能是由于理论假设中将土体视为了理想弹塑性材料,过高考虑了土体强度所致.
同时,理论值与实测值具有较高的相关性,表明本文理论可以正确的反映极限泥浆压力的变化规律,并且基于理论值与实测值的关系,可以通过理论计算得到真实的极限泥浆压力,并应用于工程实际.另外,当考虑渗流时,理论值与实测值的相关性更高,也进一步表明考虑渗流的必要性.
为分析泥浆压力、渗流作用对孔周土体应力场、位移场的影响以及强度准则选取、泥浆流变参数对泥浆压力控制问题的影响,以下将根据本文推导的公式进行算例分析.
某水厂出厂干管下穿南水北调干渠工程,采用水平定向钻穿越施工,穿越水平总长度525 m,深度为20.69 m,主要在重粉质壤土层中通过,管道采用外径为1 020 mm的钢管,按管径的1.2倍进行扩孔.由详勘报告可知,土体弹性模量E=30.8 MPa,泊松比v=0.3,粘聚力c=28 kPa,内摩擦角φ=18°,剪胀角工程上一般近似取为0.假定各向同性的初始应力P0=100 kPa.初始孔半径取设计扩孔半径r0=612 mm.
在考虑泥浆压力对孔周土体的影响时,分别取不考虑和考虑渗透压力两种情况,即分别取Pw=0和Pw=0.1P.为判断不同泥浆压力对孔周土体的影响,选取泥浆压力为200,300,400,500 kPa 进行计算,其泥浆渗透压力为0和20,30,40,50 kPa,其他参数见上文.
以G-SMP准则为例进行分析.此时,A=2.0915,B=94.063,临塑压力为165.73 kPa,极限泥浆压力分别为893.24 kPa、742.7 kPa.
在不同泥浆压力作用下径向应力、环向应力沿径向的变化规律如图3、图4所示.
图3 不同泥浆压力下径向应力沿径向的分布曲线
Fig.3 Distribution curve of radial stress along the radial direction under different mud pressures
图4 不同泥浆压力下环向应力沿径向的分布曲线
Fig.4 Distribution curve of cyclic stress along the radial direction under different mud pressures
从图3、图4中可以看出,随着距孔中心径向距离的增加,径向应力呈现非线性减小的趋势,最终稳定在初始应力值附近; 环向应力先快速减小再增加最终趋于初始应力值附近,最小值出现在弹塑性交界面.随着泥浆压力增加,径向应力明显增加,环向应力在塑性区内也显著增加.在泥浆压力的作用下,孔周土体应力变化较大,尤其在孔壁处应力变化最大,若孔壁处的应力超过土体强度,孔壁将发生失稳破坏,因此,为维持孔壁的稳定性,应严格控制好泥浆压力.同时,与不考虑渗流相比,当渗流存在时,径向应力、环向应力均减小,表明渗流体积力会对孔周土体应力场产生影响.
不同泥浆压力作用下径向位移沿径向的变化规律如图5所示.从图5中可以看出,随着距孔中心径向距离的增加,径向位移逐渐减小,最终趋于零.随着泥浆压力的增加,径向位移明显增加,当渗流为0时,P=500 kPa时孔壁处所对应的径向位移是P=200 kPa时孔壁处位移的26.8倍,可见泥浆压力对位移产生很大影响.因此,为避免孔壁处发生较大位移,泥浆压力应控制在较低值.与不考虑渗流相比,当渗流存在时,径向位移值增加,当泥浆压力为400 kPa时,孔壁处的径向位移相对增加了27.7%,可见渗流对径向位移有明显影响,在以位移为参考因素来控制泥浆压力时必须考虑渗流的影响.
根据以上分析可知泥浆压力的大小对塑性区应力、位移影响显著,尤其是孔壁处的应力和位移,为防止孔周土体发生塑性破坏,泥浆压力尽量取较小值,即取临塑压力值较优.
图5 不同泥浆压力下径向位移沿径向的分布曲线
Fig.5 Distribution curve of radial displacement along the radial direction under different mud pressures
在扩孔过程中,泥浆压力越大,形成的扩孔半径和塑性区半径越大,当泥浆压力达到极限值时,扩孔半径r1相对于初始孔半径r0无限大.当扩孔半径很大时,破坏了原有孔径,对定向钻施工不利,因此,需要事先了解泥浆压力的极限值,在施工过程中,将泥浆压力严格控制在极限值以下.
在考虑浆液渗透压力影响时,以泥浆压力为基础进行折减,对应泥浆渗透压力选用折减系数为0,0.1,0.2,0.3,0.4,0.5进行分析[29].
根据上文提及的土体参数和工程数据,利用式(31)求解泥浆压力的极限值.不同强度准则下,泥浆渗透压力对泥浆压力极限值的影响规律如图6所示.
如图6所示,随着泥浆渗透压力的增加,泥浆压力极限值呈非线性减小的趋势.当采用G-SMP准则时,泥浆渗透压力折减系数为0.5与为0时相比,泥浆压力极限值减小了50.6%,说明泥浆渗透压力对泥浆压力极限值的影响显著,因此,考虑泥浆压力控制时不能忽略泥浆渗透压力的影响.
图6 泥浆渗透压力对泥浆压力极限值的影响
Fig.6 Effect of mud seepage pressure on limit mud pressure
同时,采用不同的强度准则,泥浆压力极限值会有明显差异,以渗流为0时为例,UST1准则和G-SMP准则下的泥浆压力极限值是M-C准则下的泥浆压力极限值的1.25倍和1.17倍,可见,强度准则的选取对泥浆压力的计算有较大影响,在进行泥浆压力控制时,应根据工程地质情况选择合适的强度准则.
泥浆在钻孔内流动会存在压力损失,钻孔内任一位置处的泥浆压力Pmud可由下式计算[30]:
式中:Ppump为泥浆泵送压力; u为泥浆流速; L为泥浆经由扩孔器流至计算点处流经的距离; μ为泥浆的动力粘度; τ0为泥浆屈服应力; D为钻孔内径; d为钻杆外径.
可以看出,钻孔内的泥浆压力大小与泥浆泵送压力和泥浆流变参数有关,当泥浆压力Pmud大于极限泥浆压力Pu时,漏浆风险较高,将Pmud>Pu的钻孔区域视为泥浆压力影响区域,通过研究泥浆流变参数对该区域的影响,可从泥浆流变参数角度分析压力控制问题,为施工中配置泥浆提供参考.
图7给出了不同泥浆流变参数下泥浆压力沿远离扩孔器方向的变化情况,并通过与式(31)计算得到的泥浆极限压力值对比,得出了不同流变参数下的泥浆压力影响区域.计算参数取值[31]如表1所示.
表1 计算参数
Tab.1 Calculation parameters
从图7可以看出,当膨润土含量从3%增加至5%时,泥浆压力影响区域由80.4 m减小到了24.4 m.即增加膨润土含量(即提高泥浆粘度和屈服应力),可以显著减小泥浆压力影响区域.
图7 泥浆流变参数对泥浆压力影响区域的影响
Fig.7 Effect of mud rheological parameters on mud pressure influence area
分析可得,渗透压力和泥浆流变参数分别对泥浆极限压力值和泥浆压力影响区域存在影响,可通过增加膨润土含量来改变泥浆流变参数,提高粘度和屈服应力,以减小泥浆压力影响区域,同时,在泥浆压力影响区域内,可通过地面注浆等方式减小土体的渗透系数,减小渗透压力,提高泥浆压力极限值,避免施工中出现漏浆.
(1)随着泥浆压力的增加,径向位移明显增加,泥浆压力从200 kPa增加至500 kPa时孔壁处位移增长了25.8倍.以泥浆压力为400 kPa为例,考虑渗流作用后孔壁处的径向位移相对增加了27.7%,表明渗流影响不容忽视;
(2)泥浆渗透压力的大小对泥浆压力极限值影响显著,泥浆压力极限值随泥浆渗透压力的增大而减小,且考虑渗透压力作用的理论值与实测值相关性更高;
(3)强度准则的选取对泥浆压力的计算有较大影响,泥浆压力极限值由大至小依次为UST1准则、G-SMP准则、M-C准则,应根据工程实际情况选择合适的强度准则,避免高估或低估泥浆压力极限值;
(4)泥浆压力影响区域与泥浆流变参数存在关联,可通过增加膨润土含量,提高泥浆粘度和屈服应力的方式减小泥浆压力影响区域,同时,在泥浆压力影响区域内,减小土体的渗透系数,可减小渗透压力,提高泥浆压力极限值.
