基金项目:国家自然科学基金项目(No.51878188); 羊城学者首席科学家项目(1201541551)
第一作者:张紫祥(1994-),男,博士生,主要从事复合材料拱的稳定性研究.E-mail:zhangzixiang@e.gzhu.edu.cn 通信作者:刘爱荣(1972-),女,教授,主要从事桥梁结构防灾减灾研究.E-mail:liu-a-r@163.com
(广州大学-淡江大学 工程结构灾害与控制联合研究中心, 广东 广州 510006)
(Guangzhou University-Tamkang University Joint Research Centre for Engineering Structure Disaster Prevention and Control, Guangzhou University, Guangzhou 51006, China)
FRP; circular arches; in-plane; nonlinear buckling; theoretical solution.
DOI: 10.15986j.1006-7930.2019.02.012
本文开展了集中荷载作用下FRP圆弧拱的面内弹性失稳理论研究,基于能量变分原理建立了拱的非线性平衡方程,提出了FRP拱修正长细比计算公式,推导了拱失稳临界荷载解析解.通过有限元数值解验证了理论公式的正确性,着重分析了铺层角度、铺层厚度及矢跨比等设计参数对FRP拱失稳临界荷载的影响.研究结果表明,铺层方向显著影响拱的失稳临界荷载; 对于单种角度铺层的截面,保证铺层总厚度不变条件下,仅增加铺层数量并不会引起失稳临界荷载量值的变化; 拱矢跨比在1/10~1/3范围内变化时,失稳临界荷载随着矢跨比的增大而增大,且随着矢跨比的增加,增长速率逐渐下降.
This paper presents an analytical investigation of the in-plane elastic buckling of FRP arches subjected to a central concentrated load. The nonlinear buckling equilibrium equation is established based on energy variation principle. A new slenderness ratio formula is further proposed and the theoretical buckling load of FRP circular shallow fixed arch is derived. consequently. Numerical simulation and additional experiment are implemented to verify the accuracy of the analytical solutions derived in this context. A parametric study is then conducted to analyze the effect of ply orientation, laminated thickness, and the rise-span ratio on in-plane bucking critical load for laminated fixed circular shallow arch. It is found that the pavement condition significantly impact the buckling critical load. Increasing the number of layer only will not change the value of the critical load, with the thickness of laminated arch being constant. When the rise-span ratio varies from 1/10 to 1/3, the critical load of instability increases with the increase of span ratio, whereas the growth rate decreases with the increase of span ratio.
在现代土木工程领域,纤维增强材料以其高强、质轻、抗腐蚀等优良性能,日益成为结构选材的新宠[1].随着纤维增强材料工艺大幅改良,近年来国际上相继建成了十余座全纤维增强复合材料(FRP)拱桥(见图1).其中,以西班牙Lleida 跨线人行天桥[2],荷兰Ooypoort跨河人行单拱桥[3]及ApATeCh俄罗斯公园桥[4]最为著名.建筑结构领域,德国斯图加特大学ICD/ICKE研究展厅的弧形外壳,美国乔布斯剧院圆形碳纤维屋顶,zara香奈儿展馆玻纤外壁等均利用了FRP材料低成本化、可设计的优良特性,极大的满足了建筑形态多样化的刚性需求[5-8].然而,FRP虽然能有效减轻结构自重,增加跨越能力,但也加剧了结构失稳的风险.与蓬勃发展的FRP拱形结构的工程应用相比,目前关于FRP拱结构静力稳定性设计理论的研究仍停留在初步阶段,失稳机理尚不明确,设计缺乏依据,无法完全指导工程实际设计.
由于FRP材料性能的特殊性,FRP拱的解析解公式推导过程复杂,基本上均借助于数值模拟.Luu 等[9]基于NURBS插值等几何法,开展了考虑剪切变形影响下层合曲梁的弹性失稳数值研究.Fraternali [10]基于有限元理论,研究了双模量层合拱的非线性面内、外弹性失稳问题,分析了拉压模量比对拱后屈曲响应的影响.Sonawane [11]通过试探函数法,开展了集中荷载作用下双层复材圆弧浅拱的非线性屈曲数值研究,给出了失稳临界荷载的近似解析式,但是理论结果与有限元结果存在较大差距.Kim and Chaudhuri [12]开展了对称铺层条件下圆弧薄拱的后屈曲理论研究,由于未考虑压弯耦合矩阵,其研究结果适用性大大受限.
本文开展了集中荷载作用下固接FRP圆弧拱的面内弹性稳定理论研究,在此基础上提出了新的修正长细比公式以表征层合拱的失稳模式,通过有限元模拟结果验证了理论结果的正确性.
为便于公式推导,本文引入如下假设:
(1)各铺层之间粘接牢固,形变过程中各层不发生相对滑动.(2)各层近似处于平面应力状态.(3)变形前后直法线不变.(4)由于截面宽度b弧长S,忽略侧向泊松效应.(5)材料在形变过程中保持弹性.(6)满足平截面假定.
拱顶集中荷载作用下的FRP拱的力学模型如图2所示.本文拟采用FRP片材叠合截面,截面高度为H,宽度为B.圆弧拱的开口角为2φ,ν 和 ω分别表示中面处的径向位移和轴向位移,R是圆弧拱的初始半径,r是横截面上任意一点P(r, φ)的坐标值.
综合考虑拱失稳前非线性影响,构建FRP圆弧拱在极坐标系下膜应变εm及弯曲应变εb组成的轴向应变表达式[12-21]:
ε=εm+κρ(1)考虑拱失稳前非线性影响计入径向变形一阶导数的平方项,有
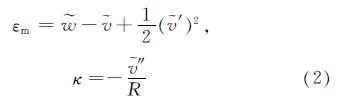
其中,εm是中面应变,κ为中面曲率,无量纲轴向及径向位移分别表示为
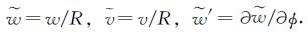
根据经典层合理论,非弹性主方向上各层等效弹性模量可表示为[22]
1/(Ek)=(cos4θk)/(E11)+(1/(G12)-(2ν12)/(E11))cos2θksin2θk+
(sin4θk)/(E22)(3)
其中, E11为弹性主方向纵向弹性模量,E22为弹性主方向横向弹性模量,G12为面内剪切模量,ν12为纵横泊松比, θ为纤维布置方向.
由于最小势能原理力学概念清晰,解法便利,较易获得收敛的解析解,因此常被用于解决结构稳定问题.基于以上优势,本文构建了拱的变形能和外力势能,建立了整体结构的势能泛函.
δW=∫φ-φ[Nδεm-Mδκ]dφ+∫φ-φDirac(θ)Qδ(~overv)dφ=0(4)
上式中,FRP拱的轴力和弯矩可以表示为
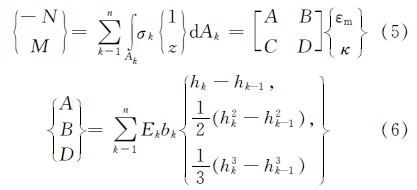
圆弧拱的固接边界条件可表示为
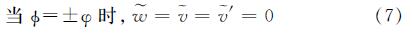
联立式(5)和式(6),求解弯矩的二阶导数:
M″=(D-(B2)/A)κ″=EI</sub>effκ″(8)
将式(8)代入式(4)并进行分部积分,引入边界条件,得出集中荷载作用下FRP圆拱的径向位移:
(~overv)=(cos(β)-cos(μφ))/(sin(β))·β/(μ2)-1/2((β2)/(μ2)-φ2)-
(QR2)/(2μ3EIeff)[(cos((β)-1)(cos(μφ)+1))/(sin(β))]-
(QR2)/(2μ2EIeff){(2H(φ)-1)[sin(μφ)-μφ]}-
(QβR2)/(2μ2EIeff)(9)
其中,Q是外部集中荷载,H为Heaviside阶跃函数.μ和 β为轴力参数,定义如下:
μ2=(NR2)/(EIeff), β=μφ(10)
由式(9)可知,径向位移(~overv)同时为N,Q及φ的函数,为了描述荷载与位移关系,沿拱轴在轴力N两侧积分有
A1P2+B1P+C1=0(11)
其中,
P=(QR2φ)/(2EIeff)=(Qπ2)/(2NE2φ), NE2=(π2EIeff)/((S/2)2)(12)
参数A1,B1,C1分别为
A1=(βcosβ-3sinβ+2β)/(2β5(cosβ+1))(13)
B1=(sinβ-β)/(2β3(cosβ+1))(14)
C1=(2βcos2β-3cosβsinβ+β)/(12βsin2β)+(β2)/(λ2)(15)
拱的修正长细比及等效回转半径定义为
λ=(Rφ2)/(rxeff)=(Sφ)/(rxeff)(16)
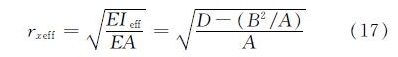
平衡路径线上的极值点可由式(11)对β求微分得出,即
A2P2+B2P+C2=0(18)
其中,
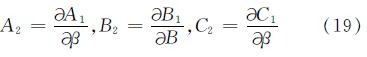
为了验证解析公式的正确性,本文采用ANSYS软件中Shell 181单元建立图3所示的有限元模型.表1给出了有限元模型采用的材料特性.通过设置Tsai-Wu失效准则,较为精确地模拟了FRP圆弧拱模型的非线性弹性失稳,跟踪了拱的失稳平衡路径曲线.
图4(a)和图4(b)分别描绘了拱顶及1/4弧长处的无量纲荷载与位移关系曲线.图4(a)所示,固接FRP圆弧拱的非线性平衡路径曲线可以分成oa, ab和bc三个分支.加载初期,无量纲拱顶位移v/f沿路径线oa随无量纲荷载Q/2Ncφ的增大而增大,抵达上极值点a后圆弧拱失稳,拱轴内部产生力差,无量纲位移 v/f 沿路径线ab随无量纲荷载Q/2Ncφ减小继续增长; 当荷载减小至下极值点b时,圆弧拱重新具备承载能力,无量纲荷载Q/2Ncφ随着无量纲拱顶径向位移v/f的增大,沿平衡路径线bc再次增大.图4(a)及4(b)表明,理论推导结果与有限元模拟结果基本吻合,推导得出的失稳临界荷载的解析式可以较为准确地描述FRP圆弧拱的失稳形式.
为了研究铺层角度对失稳临界荷载的影响,本文设计了铺层工况.以四层等厚铺层为例(见图5a),任意选择某层布置90度铺层,其余各层布置0度铺层并绘出无量纲轴力-荷载曲线.由图可知,固定边界条件下,铺层[0,90,0,0]与[0,0,90,0]承载能力相当,铺层[90,0,0,0]与[0,0,0,90]的承载能力亦相等.然而,比较铺层[0,90,0,0]及[0,0,0,90]可以发现, 90度铺层位置显著影响拱的失稳临界荷载.图5 铺层角度、铺层厚度及矢跨比对失稳临界荷载的影响
Fig.5 The effects of ply-orientation, ply-thickness, and rise-span ratios on the buckling load of FRP arch
本文还开展了矢跨比及铺层厚度对失稳临界荷载的影响研究.图5(c)显示,FRP拱的失稳临界荷载随矢跨比的增大而增大,且随着矢跨比的增大,增长速率逐渐下降.有限元结果表明,对于矢跨比小于1/4 的FRP拱,本文提出的解析式可以较为准确的预测FRP拱的失稳临界荷载.由图5(d)可知,FRP拱的失稳临界荷载随着铺层厚度的增加而增加,其增长速率亦逐渐增大.表2分析了铺层数目对单种角度铺层拱的失稳临界荷载的影响.在铺层总厚度不变条件下,增加铺层数量不会引起单种角度拱的失稳临界荷载量值的变化.
本文开展了集中荷载作用下固接FRP圆拱的面内弹性稳定的理论研究,并通过有限元模型验证了理论结果的正确性.研究结果表明,90度铺层位置显著影响拱的失稳临界荷载,对称铺层 [0,90,90,0]与[90,0,0,90]铺层条件下的失稳临界荷载差异十分明显.此外,本文还研究了铺层厚度(3~9层)及矢跨比(1/10~1/3范围内)对失稳临界荷载的影响.研究发现,FRP拱的失稳临界荷载随着铺层厚度的增加而增加,且其增长速率亦逐渐增大; 对于单种角度布置的截面,在保证铺层总厚度不变条件下,仅增加铺层数量并不会引起失稳临界荷载量值的变化.FRP拱失稳临界荷载随矢跨比的增大而增大,其随着矢跨比的增加,增长速率逐渐下降.